선형 모델을 이용한 n차 다항식의 회귀

선형 모델은 1차 다항식인 직선에 대한 모델 만을 예측할 수 있습니다. 그렇다면 직선이 아닌 곡선, 즉 2차 다항식 이상의 모델을 예측하기 위해서는 선형 모델을 사용할 수 없다고 생각할 수 있습니다. 하지만 생각과는 다르게 선형 모델로도 2차 다항식 이상의 모델도 예측할 수 있는데, 이는 약간의 발상의 전환이 필요합니다. 즉, 선형 모델의 경우 특징 변수가 1차로 다항식으로만 구성되어 있습니다. 만약 x^2와 같은 거듭제곱인 2차식의 경우일때 더 이상 선형 모델이 아니게 되지만, x^2을 z라는 1차 다항식으로 취급하게 되면 선형 모델로도 2차 이상의 다항식도 회귀분석이 가능합니다.

다음의 코드는 3차 다항식에 대한 회귀분석에 대한 코드입니다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

np.random.seed(3224)
m = 100
X = 10 * np.random.rand(m, 1) - 5
y = (-0.8 * X**3) + (0.5 * X**2) + (2 * X) - 3 + (np.random.randn(m, 1) * 10)

poly_features = PolynomialFeatures(degree=3, include_bias=False)
X_poly = poly_features.fit_transform(X)

model = LinearRegression()
model.fit(X_poly, y)

X_new = np.linspace(-5, 5, 20).reshape(20, 1)
X_new_poly = poly_features.transform(X_new)
y_new = model.predict(X_new_poly)

plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-")
plt.show()

결과는 다음과 같습니다.

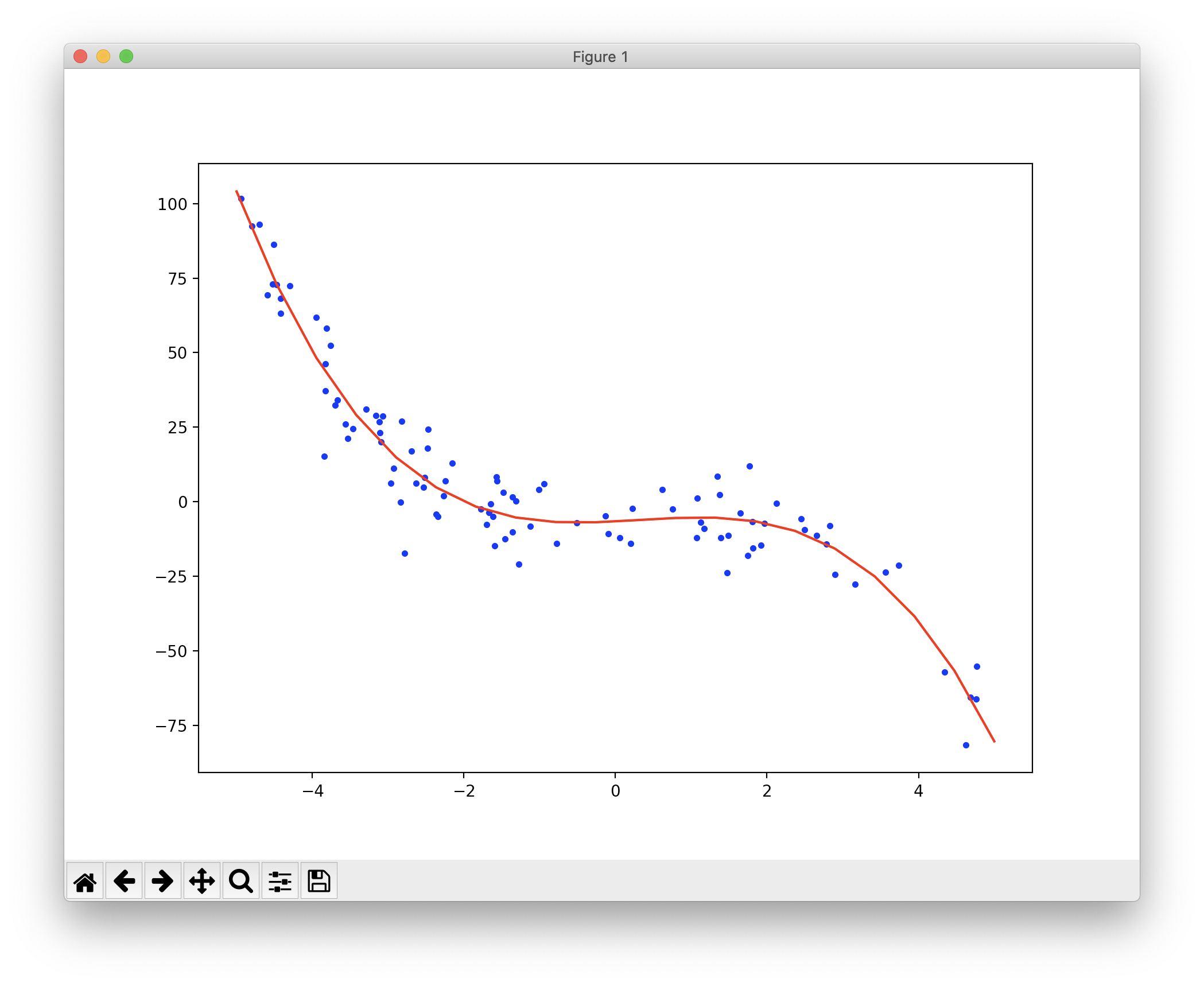
코드를 살펴보면, 6-9는 잡음이 섞인 샘플 데이터는 3차 다항식의 형태로 구성합니다. 11-12는 1개의 특성을 2차항과 3차항에 대한 독립적인 특성을 추가로 생성해 줍니다. 즉, 특성값이 2라면 4와 8이라는 특성값이 생성됩니다.