계층적 샘플링이란 모집단의 데이터 분포 비율을 유지하면서 데이터를 샘플링(취득)하는 것을 말합니다. 예를들어, 모집단의 남녀 성비가 각각 54%, 46%라고 한다면 이 모집단에서 취득한 샘플 데이터 역시 남녀 성비가 각각 54%, 46%가 되도록 하는 것입니다.
계층적 샘플링의 실제 활용은 학습 데이터와 테스트 데이터 또는 검증 데이터를 일정한 비율로 나눠 구분할때 반드시 적용되어야 합니다. 계층적 샘플링을 적용하지 않고 분할한다고 해도 확률적으로 비율이 유지될 수 있다고 기대하겠지만 이는 상황에 따라 적절한 안정장치가 되지 못합니다.
간단한 데이터셋을 통해 이 계층적 샘플링을 적용하는 내용을 정리하겠습니다. 데이터셋은 아래의 글에서 소개한 전복 데이터입니다.
위의 글에서 파악한 전복 데이터를 가져오는 코드는 다음과 같습니다.
import pandas as pd
raw_data = pd.read_csv('./datasets/datasets_1495_2672_abalone.data.csv',
names=['sex', 'tall', 'radius', 'height', 'weg1', 'weg2', 'weg3', 'weg4', 'ring_cnt'])
이제 이 데이터셋에서 지름(radius)를 총 5개의 계층으로 나누고, 분포를 시각화해봅니다. 지름을 계층적 샘플링의 기준으로 삼은 이유는 이 지금이 분석하고자 하는 결과에 가장 중요한 의미를 가진다는 어떤 판단(대표적으로 표준상관계수;Standard Correlation Coefficient 분석을 통함)에 의함입니다.
import numpy as np from sklearn.model_selection import train_test_split import matplotlib.pyplot as plt raw_data["radius_cat"] = pd.cut(raw_data["radius"], bins=[0., 0.13, 0.28, 0.35, 0.56, np.inf], labels=[1,2,3,4,5]) raw_data["radius_cat"].hist() plt.show()
[0,0.13)을 1로, [0.13,0.28]을 2로, [0.28,0.35)를 3으로, [0.35,0.56)을 4로, [0.56,inf]를 5로 계층화시킨 값을 radius_cat 컬럼에 추가하고, 각 계층별 분포 파악을 위한 히스토그램은 위 코드의 결과로써 다음과 같습니다.
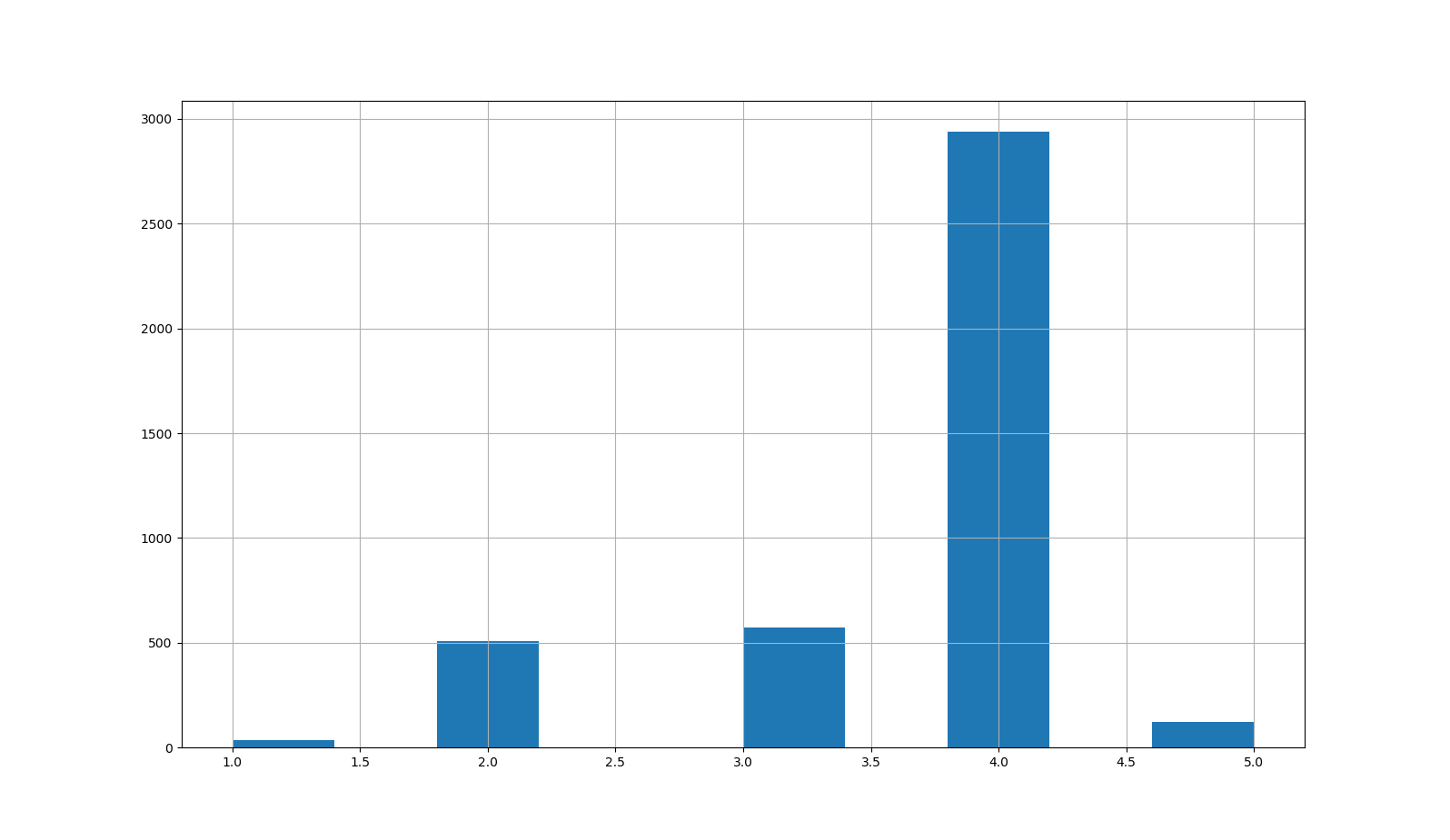
이제 이 데이터셋을 학습 데이터셋과 테스트 데이터셋으로 나누는 코드는 다음과 같습니다.
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(raw_data, raw_data["radius_cat"]):
strat_train_set = raw_data.loc[train_index]
strat_test_set = raw_data.loc[test_index]
strat_train_set["radius_cat"].hist()
plt.show()
strat_test_set["radius_cat"].hist()
plt.show()
계층적 샘플링된 학습 데이터셋과 테스트 데이터셋은 각각 strat_train_set, strat_test_set 인데요. 이 두 데이터셋에 대한 분포를 히스트그램으로 표시해 보면 다음과 같습니다.
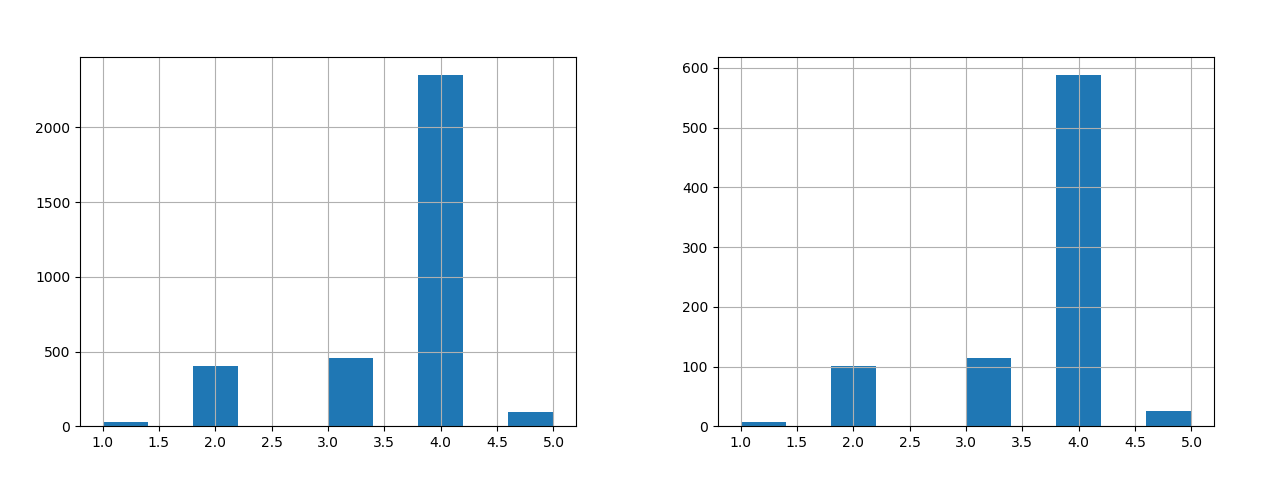
위의 결과를 보면 시각적으로도 학습 데이터셋과 테스트 데이터셋에서 지름에 대한 컬럼에 대해 원본 데이터셋과 동일 비율로 구성되고 있다는 것을 알 수 있습니다.
앞서 계층적 샘플링을 위해 추가한 radius_cat 필드는 더 이상 필요치 않으므로 다음 코드를 통해 제거할 수 있습니다.
for d in (strat_train_set, strat_test_set):
d.drop("radius_cat", axis=1, inplace=True)
끝으로 특성간의 상관관계를 조사하기 위한 방법은 아래 글을 참고 하기 바랍니다.
