[GIS] 가중치 최소 비용 경로 분석(Weighted Lowest Cost Path Analysis)

공간상의 어떤 지점을 통과하기 위해 드는 비용 값이 있다고 해 보겠습니다. 일단 어떤 지점을 통과한다는 것은 그 공간의 거리가 길수록 통과하는데 더 많은 비용이 들고, 거리가 짤을 수록 통과하는데 더 작은 비용이 듭니다.

여기에… 이 거리에 대한 비용은 기본적으로 반영하되, 그 지점을 통화하는데 드는 또 다른 비용을 추가적으로 고려하여, 임이의 지점에서 어떤 특정한 지점으로 이동할때 가장 최소의 비용이 드는 경로를 분석해 보는 것을 고민해 볼 필요가 있습니다.

여기서 또 다른 비용은 그 대상이 되는 분석에 따라 매우 다양한데, 쉽게 생각해볼 수 있는 것이 지형의 경사(Slope)입니다. 예를들어서, 노약자가 어느 지점에서 특정한 지점으로 이동할때… 단순히 가장 짧은 거리가 아닌 지형이 좀더 완만~한 경로를 선택해 가는것이 효율적이라 할 수 있겠습니다.

이 예에서 지형의 강사값이 바로 어느 지점을 통과하는데 드는 기본적인 비용인 거리에 대한 가중치로써의 역활을 한다는 점에서…. 이러한 분석을 “가중치 최소 비용 경로 분석(Weighted Lowest Cost  Path Analysis)”이라고 이름을 붙일 수 있겠습니다.

간단히 WLCP라고 하는 이 분석은 공간을 대상으로 하는 GIS 분석에서 매우 가치 있게 활용됩니다. 간단한 예로써 어떤 고객이 자신이 살고 있는 집에서 주위의 마트 중에 어느 마트에 갈것인지를 결정하거나 예측하는 경우를 생각해 보겠습니다.

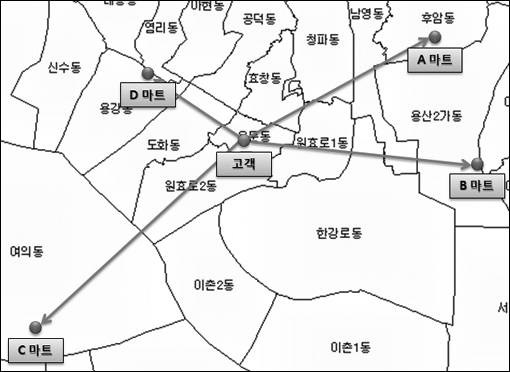
위의 그림은 고객(화면 가운데의 용문동에 위치)이 갈 수 있는 주위의 4개의 마트를 표시한 것입니다. 고객과 마트의 거리만을 놓고 볼때 D 마트가 가장 가까워 고객은 D 마트로 방문할 가능성이 가장 큽니다.

하지만 고객은 이처럼 단순히 거리만 가깝다는 이유로 꼭 그 마트를 방문하지는 않습니다. 여기에는 다양한 변수가 존재하는데, 그 변수는 해당 마트까지 가는 것까지의 교통혼잡지수나 마트가 존재하는 지역의 문화 수준이나 생활 수준, 또는 해당 마트가 생필품을 주로 판매하는지, 아니면 고가의 사치품을 주로 판매하는지 등과 같은 변수가 작용하여, 고객은 자신이 방문할 방문할 마트를  결정하게 됩니다. 이러한 교통혼잡지수와 문화 수준, 생활 수준 등이 바로 WLCP 분석을 위한 가중치가 됩니다.

WLCP의 근본적인 필요성인, 최소의 경비가 소요되는 길을 찾는 것 뿐만 아니라.. 이 방법을 응용하여 길을 찾는 것이 아닌 반대로.. 어느 지점에 마트를 세워야 하는지 등과 같은 최적입지 분석이나 최적입지에 세워졌는지에 대한 검증 분석에도 충분히 활용될 수 있습니다. 문제는 얼마나 다양하고 정확하며, 꼭 필요한 가중치 변수를 사용하느냐가 문제이며.. 이 변수 선택의 몫은 이 변수들에 대해 가장 잘 알고 있는 해당 분야의 전문가의 몫일 것입니다.

만약 기회가 닿는다면, 개발 맵 엔진에 이 WLCP 분석을 확장기능으로써 개발하고, 간단히 어떤 지점에서 목적지까지  가장 경사가 완만한… 최단 거리를 구하는 예를 통해 검증해 보도록 하겠습니다.