이 글은 두 선분의 교차점을 구하는 알고리즘이 작업에 필요해서 작성해둔 글이다. 참고로, 예전에 두선분의 교차점을 구하는 것 자체가 쉬울 것으로 생각하고 흔히 생각하는 기울기, y 절편을 이용하여 접근하려고 하였다. 이는 상당히 비효율적 방법이였고 조금 더 효율적인 방법으로 접근하였다.
먼저 직선의 방정식으로써, 기울기와 절편으로 나타내지 말고, t 매개변수를 이용해 나타내면 다음과 같다.
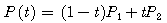
P1과 P2는 직선의 시작점과 끝점을 나타내며, t의 범위는 0에서 1까지이다. (P1, P2에서 1, 2는 아래첨자로 생각하기 바란다)
선의 식을 알았으니, 이제 두선의 교점을 구해보는 것으로 응용해보자. 먼저 아래 그림을 보자.
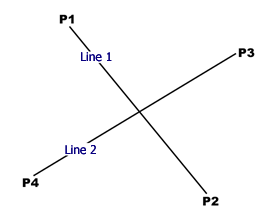
Line1은 P1과 P2로 이루어져 있으며, Line2는 P3와 P4로 이루어져 있다. 두개의 라인을 식으로 표현해보면 다음과 같다.
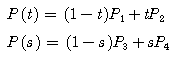
이미 알겠지만, t와 s는 0에서 1부터의 값이며, 두선의 교점은 두선의 공통된 값이므로 P(t)와 P(s)는 같으므로 위의 2개의 식은 아래의 1개의 식으로 나타낼 수 있다.
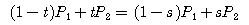
다시 위의 식을 x, y로 분리해보면 아래와 같은 두개의 식들로 분리된다.
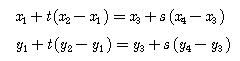
위의 식을 t와 s에 대해서 정리를 해보면 다음과 같다.
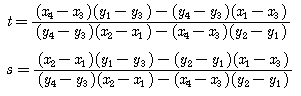
즉, 위의 t와 s는 두선이 서로 만날때의 값이므로, 최종적으로 두선의 교점은 다음과 같이 나타낼 수 있다.
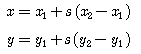
위의 x, y가 우리가 구하고자하는 두 직선의 교점이다.
마지막으로 t와 s에 대해 정리해 보도록 하자.
s와 t의 값이 0과 1 사이를 벗어나는 경우, 두 선은 교차하지 않는다고 판정해야 한다. 그리고 s와 t를 구하는 공식에서 분모가 0인 경우 두 선은 평행하다는 의미이므로 교점은 존재하지 않다. 분모와 분자 모두 0인 경우 두 선은 동일한 선이다.
아래의 코드는 위의 설명을 토대로 작성하였다.
bool GetIntersectPoint(const POINT& AP1, const POINT& AP2,
const POINT& BP1, const POINT& BP2, POINT* IP)
{
double t;
double s;
double under = (BP2.y-BP1.y)*(AP2.x-AP1.x)-(BP2.x-BP1.x)*(AP2.y-AP1.y);
if(under==0) return false;
double _t = (BP2.x-BP1.x)*(AP1.y-BP1.y) - (BP2.y-BP1.y)*(AP1.x-BP1.x);
double _s = (AP2.x-AP1.x)*(AP1.y-BP1.y) - (AP2.y-AP1.y)*(AP1.x-BP1.x);
t = _t/under;
s = _s/under;
if(t<0.0 || t>1.0 || s<0.0 || s>1.0) return false;
if(_t==0 && _s==0) return false;
IP->x = AP1.x + t * (double)(AP2.x-AP1.x);
IP->y = AP1.y + t * (double)(AP2.y-AP1.y);
return true;
}

트랙백을 할 줄 몰라서 이상하게 됐습니다. -_-;; 삭제 부탁드려요… 죄송합니다.
자료 고맙습니다~ 유용하게 잘 썼습니다~
도배삼가
코드 정말 잘 이용하고 있습니다.
한가지 문제점이 있는데,
선분이 다른 선분을 포함하는 경우( 기울기가 같은 경우에만 발생 )
위의 코드는 false를 리턴하도록 돼있더군요.
이 부분에 약간의 보완이 필요할 것 같습니다.
네, ^^ 그렇군요. 위의 함수는 교차점을 구하는 함수인지라.. 교차점이 무한 개인 경우는 교차점 없는 것으로 판단하기 때문에 false를 리턴합니다. 말씀하신 경우와 같은 문제점이나 오해가 분명이 존재할거라 판단되네요. 좋은 댓글 감사합니다~
t,s는 단지 t와 s만을 좌항에 남기고 정리한 것 뿐이랍니다. 먼저 가장 처음에 언급된 직선의 방정식을 이해하고 받아들이시는게 관건인듯합니다. 가장 잘 나온 책은 고등수학 학습서인것같습니다. 댓글 감사합니다~ ^^
정말 정말 필요한 내용이였는데 정말 감사합니다.
출처 적고 블로그에 퍼가도 될까요?
라고 묻고 이미 퍼가고 있습니다 –;;;
자유롭게 퍼가셔도 됩니다. 출처라도 살포시 남겨주시면 되구요~ ^^
좋은 글 감사드립니다.
출처를 밝히고 저의 개인 블로그에 제가 필요한 대로 수정한 내용으로 올렸는데(나중에 제가 참고할 요량으로), 양해 부탁드립니다.
댓글 감사합니다. 양해까지 부탁하지 않으셔도 되니 염려마시고 맘껏 퍼가셔도 됩니다.
저도 써먹었네요~
지식 감사합니다.^^ 퍼갈게요~
네, 이 글이 도움이 되셨다니 좋습니다.
좋은글 감사합니다. 딱 찾던 내용이네요.
스크랩해 갈께요. 출처도 함께 기록해 두겠습니다.
출처만 남겨주신다면 맘껏 퍼가셔도 됩니다.
under가 뭐에요? 아.. 너무 어렵다
이미 알겠지만, t와 s는 0에서 1부터의 값이며, 두선의 교점은 두선의 공통된 값이므로 P(t)와 P(s)는 같으므로 위의 2개의 식은 아래의 1개의 식으로 나타낼 수 있다.
까지는 이해햇는데
다시 위의 식을 x, y로 분리해보면 아래와 같은 두개의 식들로 분리된다. 부터
위의 식을 t와 s에 대해서 정리를 해보면 다음과 같다. 까지가 이해가 안되네요
x y로 어떻게 분리하길래.. 정말 너무 궁금합니다 어제부터 오늘 하루젱일 보면서 공부중이에요
아 다시 위의 식을 x, y로 분리해보면 아래와 같은 두개의 식들로 분리된다. 는 어느정도 이해했는데
위의 식을 t와 s에 대해서 정리를 해보면 다음과 같다.
이게 이해가 안되네요 t s로 정리 헠헠 진짜 빡세다
아 다 알았어요..
와 진짜 감탄스럽습니다 와.. 진짜 대단하다
어떻게 이런 생각을 수학 천재심
잘배워갑니다 고맙습니다
수학을 공부하는거랑 수학을 프로그래밍으로 짜는거랑 전혀 다른것 같아요
아무리 수학공부를해도 이런걸 짤수가 없는데
도대체 어떻게해야 이런 경지에 이르나요?
이미 알겠지만, t와 s는 0에서 1부터의 값이며, 두선의 교점은 두선의 공통된 값이므로 P(t)와 P(s)는 같으므로 위의 2개의 식은 아래의 1개의 식으로 나타낼 수 있다.
다음의 공식에서 오른쪽이 P3,P4인데 P1,P2로 되어있는거 같네요
안녕하세요, 김형준입니다.
말씀하신 부분이 맞습니다.
내용 중 오타가 있네요.
글 내용을 쫓다보면 오타임을 알 수 있으니 다행입니다..
오타 알려주셔서 감사합니다.
t의 범위는 왜 0~1 까지인가요?
선분의 정의 시에 2개의 좌표를 통해 정의되는데..
이 2개의 좌표계 선분의 시작점과 끝점입니다.
시작점은 t가 0일때, 끝점은 t=1일때입니다.
결론을 통해 t의 범위를 유추할수있는 방법이고..
선분을 구성하는 t의 범위 제한은 사실 없습니다.
under가 0일 때 동일한 선인지 확인하는 코드 입니다.
p1 p2를 지나는 선과 p3가 얼마나 떨어져 있는지 확인하려면 크로스 프로덕을 하면 알 수 있습니다.
참고로 코드를 추가 합니다.
if (under == 0)
{
PtVector3 v1, v2, c;
v1 = AP2 – AP1;
v2 = BP1 – AP1;
c = v1.Cross(v2);
if (c.DoubleLength() == 0)
{
if (v1.Dot(v2) > 0)
*IP = BP1;
else
*IP = AP1;
return true;
}
return false;
}
감사합니다. 덕분에 교차점을 잘 구했습니다!
먼저 직선의 방정식으로써, 기울기와 절편으로 나타내지 말고, t 매개변수를 이용해 나타내면 다음과 같다
P(t) = (1-t)P1 + tP2 >> 공식이 어떻게 나온건가요 ? ㅜㅜ
안녕하세요, 직선의 방정식을 검색해보시면, 그 형태 중 하나랍니다.
한 직선에 t 라는 점이 있다고 가정해서 나온 내분점 공식 이네요.
코드를 작성하기 전, 알고리즘을 이해할 수 있게 수학적 증명을 같이 써주셔서 감사합니다.
다만, 수학적 증명에 일부 아래첨자가 잘못된것 같은데 확인 부탁드리겠습니다.
*** 수정사항 1 => P(t) = P(s) 관계로부터 교차점을 기술하는 부분
(본문 내용) : (1-t)P1+tP2 = (1-s)P1 + sP2
(수정) : (1-t)P1+tP2 = (1-s)P3 + sP4
*** 수정사항 2 => 최종적으로 두선의 교점을 구하는 부분
(본문 내용) : x = x1 + s(x2 – x1)
y = y1 + s(y2 – y1)
(수정) : x = x1 + t(x2 – x1)
y = y1 + t(y2 – y1)
: Code에서는 x,y 좌표를 구할때, (x1,y1),(x2,y2),t를 이용해서 구하고 있어,
오류는 없는것 같습니다.
단순히, 수학증명을 써주실때 아래첨자를 잘못 쓰신거 같아요.
저도 코드는 안보고
본문 수학적 증명만 보고 코드로 짯다가 안되길래
왜 안되나 하고 한참 찾다가 코드보고 s 가 아니라 t 곱하는거 알았네요 ㅋㅋ
내용 잘 봤습니다. 하나 궁금한 점이 있습니다.
/**************************************************************/
위의 식을 t와 s에 대해서 정리를 해보면 다음과 같다.
/**************************************************************/
이 문장의 아래가 어떻게 나오는 지 궁금합니다.
물어보는 것이 너무 초보적인 것이라 물어볼 까 고민하다 여쭤봅니다.
오래된 글이라 명확하진 않지만.. t,s라는 변수가 있고 식이 2개이므로 식 하나를 t로 정리하고 다른 식의 t에 먼저 정리한 식을 대입해서 얻은 것으로 생각됩니다.