IDW는 이미 알고 있는 값으로부터 알고자 하는 값을 보간하는 방법입니다. IDW를 사용하여 주어진 점 x에 대한 보간된 값 u를 결정하는 일반화된 형태의 보간 함수는 다음과 같습니다.
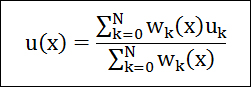
N은 이미 알고 있는 값의 개수, w는 가중치의 값, u는 앞서 말한 계산되어 나온 보간된 값입니다. IDW에서 중요한것은 가중치의 값에 해당되는 w에 대한 함수가 여러개 존재하며, Spepard 방식과 Liszka 방식 그리고 이들의 변종이 존재합니다. 여기서는 Spepard 방식에 대한 w값에 대해서만 살펴 보겠습니다.
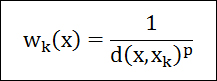
위의 식이 Spepard님이 정의한 가중치 w의 값입니다. d는 보간하고자 하는 지점(x)와 이미 알고 있는 지점(xk) 사이의 공간적 거리입니다. 바로 거리(Distance)의 역(Inverse)에 대한 가중치(Weighting)라는 의미로 IDW가 된 것입니다.
p는 0보다 큰 실수값입니다. 이 p값의 범위에 따라 전체적인 보간된 양상이 다양하게 결정됩니다. p의 범위가 0~1이면 전체적인 양상이 좁고 날카로우며 1보다 크면 넓고 부드럽게 퍼져서 보간이 됩니다. 눈에 보이는 보간된 양상을 글로써 표현하려니 한계가 있는데… 이 부분에 대해서 실제 구현을 통해 살펴보도록 하겠습니다.
끝으로 IDW처럼, 이미 알고 있는 값을 통해 다른 값을 추정(보간)하는 방법 중 Kriging 기법이 있습니다. 기회가 닿는 다면 이 Kriging 기법에 대해서도 논의해 보고 싶습니다.


형준님 블로그나, 다른 곳에서 형준님 정보를 많이 얻고 갑니다.. 매번 글 남기지 못 해서 죄송합니다. 너무 감사하단 말씀 전하고 싶네요..
철원님 댓글 정말 감사합니다.
감사합니다. 공유된 자료 덕분에 쉽게 해결했습니다. 복 많이 받으세요^^
네, 감사합니다. 익황님도 새해 복많이 받으시길..