시작점에서 어떤 방향으로 무한히 뻗어 나가는 선을 편선(Ray)이라고하자. 시작점 p와 방향벡터 d로 정의된 편선이 있을때, 이 편선이 구(Sphere)와 교차하는지 확인하는 방법에 대해 생각해보자. 교차한다면 교차점은 하나 인가, 아니면 두개인가? 아래의 그림은 여개의 상황을 보여준다.
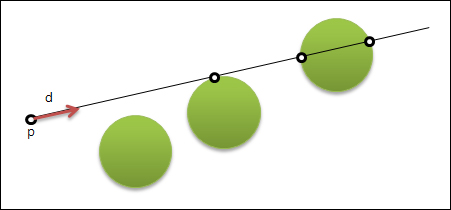
첫번째 질문은 편선과 구가 교차하는지의 여부인데, 이를 위해서 구의 중심점에서 편선까지의 거리를 구해야만 한다. 만약 그 거리가 구의 반지름보다 크다면 교차하지 않는다고 할 수 있다.
거리를 구하기 위해, 2가지 경우를 고려해야 하는데… 구의 중심점이 편선에 투영되는지 투영되지 않는지이다. 이는 내적을 통해 알 수 있다.
구의 중심점을 c라고 하고, p에서 c까지 가는 벡터를 v라고 하자. 그렇다면 만약…….
- d ∙ v > 0 이면 투영되므로 거리를 구할 수 있다는 것이고
- d ∙ v <= 0 이면 편선 뒤에 구가 있어 투영되지 않아 거리를 구할 수 없다는 것이다.
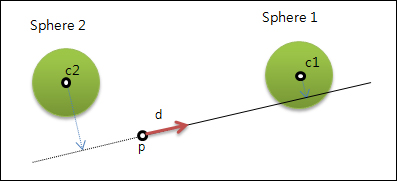
위의 두 경에 대해서 편선과 구와의 교차에 대해 살펴보도록 하자.
구의 중심점이 편선에 투영될 경우
아래의 그림은 투영될 경우에 대해서 가능한 3가지 경우이다. 구A는 교차하지 않는 것이고, 구B는 한 점에서만 교차하고 구C는 2점에서 교차한다.
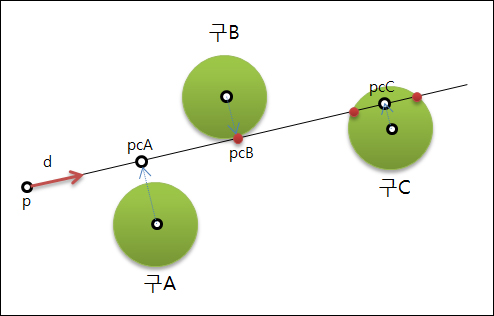
편선 위에 구의 중심점의 투영을 계산해보자. pc를 투영된 점이라고 하면, 구A에 대한 편선 위의 투영점은 pcA이고 구B에 대한 것은 pcB, 구C에 대한 것은 pcC가 된다. pc에서 구의 중심점까지의 거리가 구의 반지름보다 크다면 교차하지 않는 것이고 구A가 그렇다. pc에서 구의 중심점까지의 거리가 구의 반지름과 같다면 한점에서 만나는 것이고 구B가 그 경우이고 교차점은 점 pc이다.
구C에 대한 경우는 반지름보다 그 거리가 작은 경우이고 2개의 교차점이 존재하며 이 2개의 교차점을 구하기 위해서는 좀더 생각을 해야 하는데… 다음과 같다.
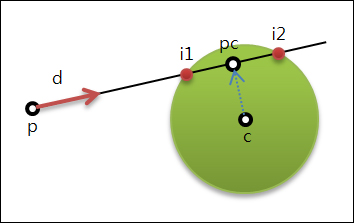
먼저 점 pc는 내적을 이용한 투영을 통해 구할 수 있다. 투영법은 이 블로그의 투영에 관한 글을 참조하기 바란다. 그리고 두개의 교차점을 i1, i2라고 하자. 다음의 과정을 통해 i1을 얻을 수 있다.
p에서 i1까지 거리를 알고 있다고 가정하면, 이 거리를 di1이라고 하고 i1은 다음 공식을 통해 구할 수 있다.
위의 공식에서 p와 d는 이미 알고 있으므로, di1을 구하는 것만 남게 된다. 점i1, pc, c로 구성된 삼각형이 직각삼각형이므로, 피타고라스(Pythagorean) 공식을 적용해보면, 삼각형의 변의 길이를 a,b,c라고 할때…
- a = |c – i1| = 구의 반지름값
- b = |pc – c|
- c = |pc – i1|
위에서 오직 길이 c만이 미지수이며, 길이 c는 다음처럼 계산할 수 있다.
그림을 통해 di1은 다음과 같음을 알수있다.
앞서 계산한 di1은 편선의 시작점(p)가 구의 내부에 있지 않다고 가정한 것이다. 만약 p가 구 안쪽에 있다면 di1에 대한 계산은 아래처럼 달라진다.
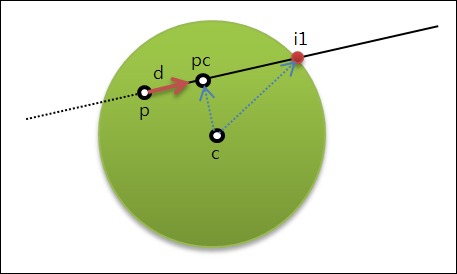
구의 중심점이 편선에 투영되지 않는 경우
구의 중심점이 편선에 투영되지 않는 경우, 편선의 시작점이 구의 외부에 위치한다면 편선과 구가 교차하지 않는다는 것이다. 반면에… 편선의 시작점 p와 구의 중심점 c까지의 거리가 구의 반지름과 작거나 같다면 교차점이 존재한다. 같다면 p 자체가 교차점이다.
편선의 시작점이 구의 내부에 위치한다면, 앞의 구의 중섬점이 편선에 투영되는 경우와 같은 방법을 적용하여 교차점을 구할 수 있다. 아래 그림을 살펴면…
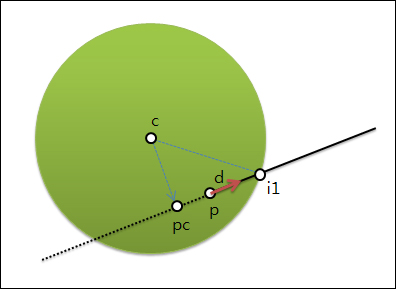
pc에서 i1까지의 거리 계산은 앞에서 본 것과 동일하다. 거리를 dist로 놓고.. di1은 다음처럼 계산할 수 있다.

저는 2차원 계측과 관련해서 프로그램을 하고 있는데요. 많은 도움이 되네요
도움이 많이 되신다니 다행이구요~ 2차원 계측… 하니 예전 대학교 입학할때 제어계측과에 입학하고 싶었던 기억이 나네요. 2차원 계측과 관련이 있을지는 모르겠지만 말입니다~ 댓글 감사드립니다~ ^^
잘 설명해 놓으셧네요 ㅎㅎ
감사합니다. 개발하다가 찾은 자료를 프로젝트에 적용하기에 앞서 정리한 글입니다.