현재 딥러닝에서 분류에 대해 가장 흔히 사용되는 손실함수는 Cross Entropy Error(CEE)입니다. CEE를 비롯하여 다른 손실함수를 간단이 정리하는 글은 아래와 같습니다.
다시, CEE에 대한 공식을 언급하면 다음과 같습니다.
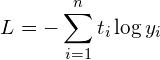
t는 정답 값이고, y는 추론 값입니다. 정답의 개수와 추론의 개수는 당연이 같구요. 이 개수가 2개이면 이진분류이고 2개보다 많으면 다중분류입니다. y값은 신경망 여러 개를 거쳐 산출된 값이 최종 마지막 어떤 특별한 활성함수의 입력값이 되어 산출된 결과값입니다. 이진분류로 가장 많이 사용되는 활성함수는 Sigmoid이고 다중분류로 가장 많이 사용되는 것이 Softmax입니다. 이러한 활성화 함수에 대한 글은 아래와 같습니다.
CEE는 추론값과 그에 대한 정답값들에 대한 연산의 합입니다. 즉, 추론값과 정답값 사이의 괴리(손실)을 합한것입니다. 이진분류는 추론값과 정답값이 2개로, 하나는 참이고 두번째는 거짓입니다. 참은 1이고 거짓은 0값입니다. 이 이진분류를 CEE로 나타내면 다음과 같습니다.
![]()
진관적으로 이해할 수 없다면, 각각의 경우로 구체화하여 이해할 수 있는데, 다행이 구체화할 경우의 수가 2가지입니다. 즉, 참일때(t=1) L은 -logy가 되고, 거짓일때(t=0) L은 -log(1-y)가 됩니다. 이것은 무엇을 의미할까요? log 그래프를 보면 다음과 같습니다.
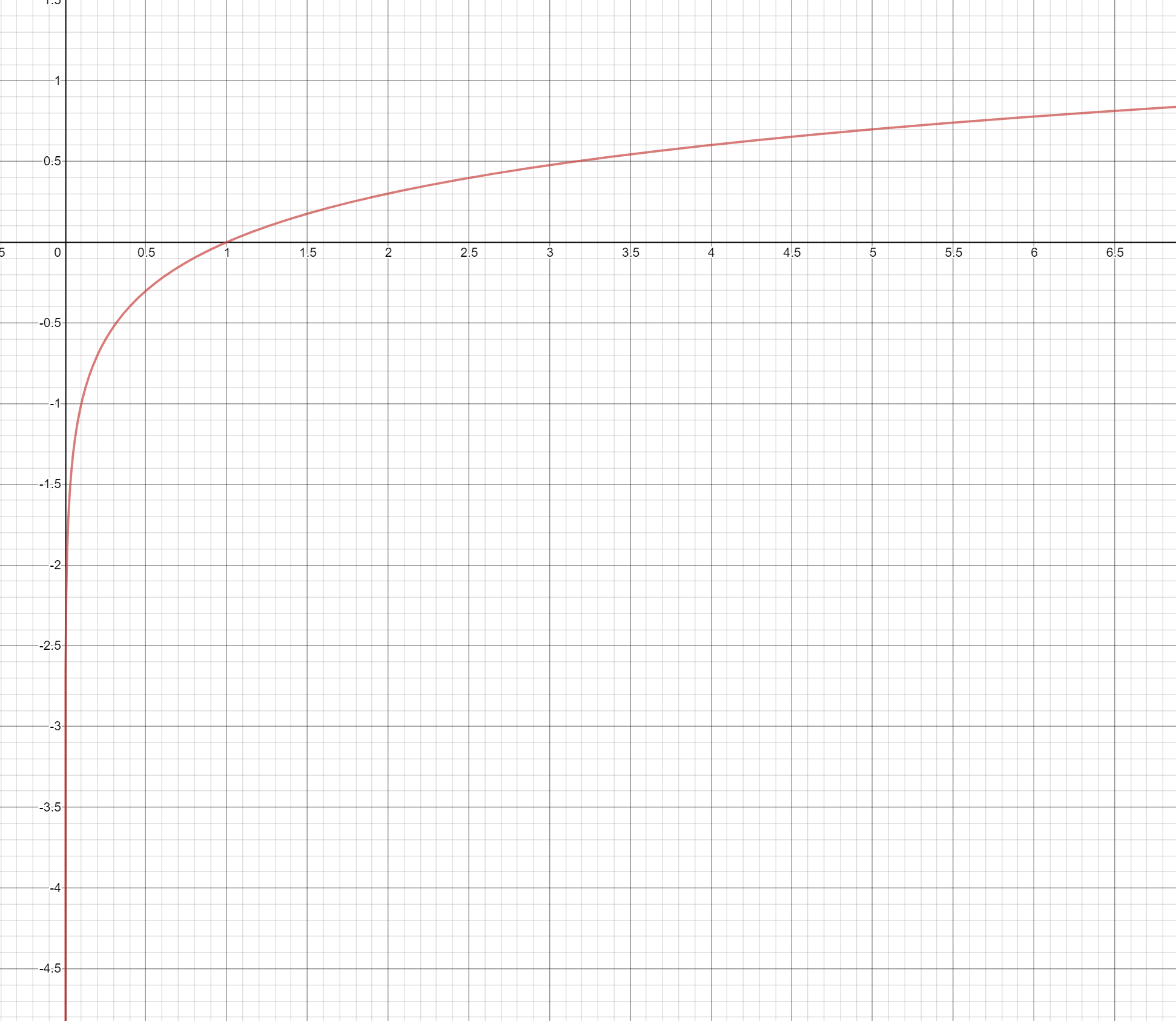
y는 Sigmoid와 Softmax의 결과이므로 값의 범위는 0~1사이입니다. 0은 무한대이고, 1은 0이입니다. 즉 참일때 y가 1(참)에 가까울 수록 L(손실, 오류)은 0에 가까워지고 y가 0(거짓)에 가까울 수록 L은 무한대에 가까워집니다. 또한 거짓일때 y가 1(참)에 가까울 수록 L(손실, 오류)은 무한대에 가까워지고 y가 0(거짓)에 가까울 수록 L은 0 가까워집니다. 손실함수의 기반과 정확이 일치한다는 것일 알 수 있습니다.

친절한 설명 덕분에 이해 되었습니다!
감사합니다!