선에 대한 수학적 설명

선에 대한 수학적 표현인, 선에 대한 방정식은 좌표와 벡터로 설명될 수 있습니다. 어떤 선이 있다고 해 보면, 그 선이 점p를 지나고 선의 방향은 벡터v라고 한다면 아래 그림처럼 상상해 볼 수 있습니다.

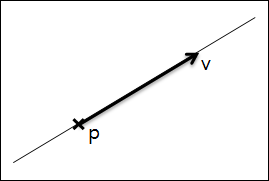
아래의 공식은 선을 구성하는 좌표를 얻는데 사용할 수 있습니다.

t는 스칼라입니다. t값에 의해 선 상의 모든 좌표를 얻을 수 있습니다. t가 0이면 좌표 p가 얻어집니다. t가 0이 아닌 다른 값이면 선 상의 다른 좌표가 얻어집니다. 백터는 2개의 좌표로부터 생성되어지므로 v는 선을 지나는 2개의 좌표를 통해 얻어집니다. p이외에 선을 지나는 다른 한 점을 p1이라고 하면 v는 p1 – p가 됩니다.

선은 양쪽 방향으로 계속 이어지며 확장된다는 것이고 광선(Ray)은 한 방향으로만 계속 이어지며 확장된다는 것으로 정의할 수 있습니다.

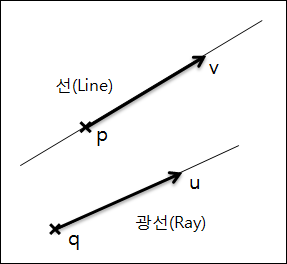
위의 그림에서 상단은 선이고 하단은 광선입니다. 위의 공식을 통해 다시 살펴보면, 선과 광선의 차이점은 t가 가질수 있는 값의 범위가 다르다는 점입니다. 선에서 t는 제한이 없으며, 광선에서 t는 음수가 될 수 없습니다.

선과 어떤 좌표 사이의 최단 거리

어떤 좌표와 어떤 선 사이의 가장 짧은 거리는 그 좌표에서 그 선에 수직인, 선 상의 좌표로 구성되는 선분의 길이입니다. 좌표p와 백터v로부터 정의되는 선에 대해서 살펴보겠습니다. 어떤 좌표q에서 이 선(좌표p와 벡터v로 결정)까지의 거리를 계산하는 것이 목표입니다.

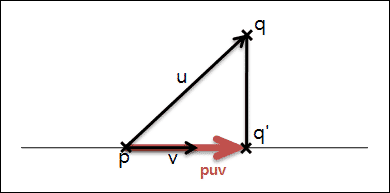
위의 그림은 좌표q에서 선까지의 거리가 좌표q와 좌표q’까지의 거리임을 보여줍니다. 좌표q’는 백터u를 백터v에 대해서 투영함으로써 얻어집니다. 백터간의 투영에 대해서는 이미 알고 있다고 가정하고 만약 모르신다면 이 블로그의 글을 참조하시길 바랍니다. 여하튼, 이 투영된 벡터 puv는 다음과 같습니다.

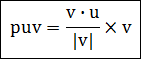
이제 q’는 아래처럼 정해질 수 있습니다.

이제 최단 거리는 q와 q’ 사이의 거리가 됩니다.

광선과 좌표 사이의 최단 거리

최단거리의 결과로 광선에 대해서 투영된 좌표들에 대해 동일한 결과 공식을 예상했으나, 다음 그림에서 보는 것처럼 항상 옳바르지는 않습니다.

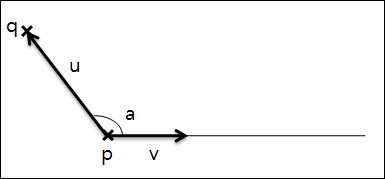
앞서 어떤 좌표q와 선 사이의 거리를 위해 제시된 공식은 오직 광선 내에서 투영될 수 있을때만 의미가 있습니다. 백터u와 백터v에 대한 내적을 통해서 광선 내에서 투영되는지 검사할 수 있습니다. 즉, 백터 u와 v 사이의 코사인 각도가 음수라면 광선 내에서 투영되지 않는다는 것입니다. 코사인 각이 음수여서 광선에 투영되지 않는다면, 좌표q에서 그 광선까지의 최단 거리는 좌표q에서 광선의 시작점까지의 거리를 계산해서 쉽게 알 수 있습니다.