두개의 벡터에 대한 외적은 또 하나의 새로운 벡터를 정의합니다. 두개의 벡터가 이루는 하나의 평면에 대해 수직인 벡터가 바로 외적에 의해 만들어지는 새로운 벡터입니다. 외적은 두 벡터가 이루는 각을 구하는 것이라든지, 광원에 대한 계산, 즉 빛의 방향을 구하는 계산 등에 응용됩니다.
아래의 공식은 두개의 벡터 v1, v2에 대한 외적 v를 구하기 위해 필요한 과정을 보여주고 있습니다. 외적 연산의 기호는 ‘ X ‘를 일반적으로 많이 사용합니다.
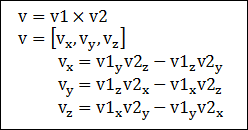
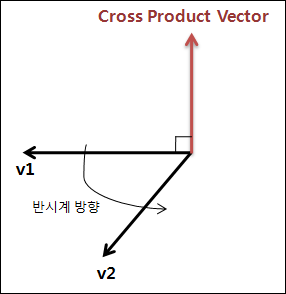
벡터 v1과 v2의 시작점을 원점이라고 할때, 벡터v1과 v2가 이루는 평면이 X축과 Z축이 구성하는 평면인 XZ라고 하면 외적에 의한 벡터는 v1에서 v2가 반시계방향이면 Y축 방향으로 위를 향하고 시계방향이면 Y축 방향으로 아래를 향합니다. 두 벡터의 외적에 대한 일반적인 성질은 아래와 같습니다. 내적과는 다르게 외적은 교환법칙이 성립하지 않습니다. 아래의 식에서 k는 스칼라값입니다.
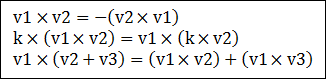
벡터v1과 v2가 이루는 사인각으로도 외적을 표시할 수 있으며, 다음과 같습니다.
![]()
위의 식에서 a가 두벡터 사이의 각도 입니다. 위 공식에서 보듯, 외적도 내적과 마찬가지로 두 벡터가 이루는 각을 구하는데 사용할 수 있습니다.

정말 큰 도움 되었습니다 고맙습니다^^
도움 되셨다니 기쁩니다~ 댓글 감사드립니다~ ^^
외적을 처음 보는 입장으로선 이해가 잘 안 갑니다..
강연수님, 어느 부분이 이해가 않가시나요? 알려주시면 능력 닿는대로 설명해 드리련만… 외적은 내적과 함께 중요한 부분을 차지하니 꼭 잘~ 이해하시길 바랍니당.. ^^
두벡터 v1,v2가 3차원좌표로 표현되어 있는데 그냥 두벡터를 한평면위에 올려놨다고 생각하고 외적을 구하는건가요? 그리고 벡터를 행렬식으로도 풀던데 그방법도 아시면 좀 알려주세요 ㅠㅠ
두 벡터를 통해 하나의 유일한 평면이 정의됩니다. 그리고 벡터를 행렬식으로 푸는 방법은 벡터의 요소를 하나 추가한(w) 동차좌표계로 변환해서 행렬식과 곱하게 됩니다. 음… 보다 정확한건 구글에서 벡터, 동차좌표계로 검색해보시면 감을 잡으실 수 있으리라 생각됩니다~
^^ 감사합니다~
완젼 감사요! ㅋㅋㅋ
네, 수학 재미있죠? ^^