평면의 방정식은 아래처럼 기술할 수 있으며, (A, B, C)는 평면에 대한 법선(수직) 백터이고.. D는 이 법선 백터의 길이(크기)입니다. (x,y,z)는 평면상의 임이의 점입니다.
![]()
평면은 최소한 점 3개가 정해지면 평면의 방정식이 명확히 정의됩니다. 즉, 평면 상의 (x1,y1,z1)과 (x2, y2, z2) 그리고 (x3, y3, z3)가 정해지면 위의 공식에서 A, B, C, D의 값이 정해진다는 의미입니다. 각 A,B,C,D는 정해진 점들에 대해서 다음과 같은 행렬식으로 정의되며…
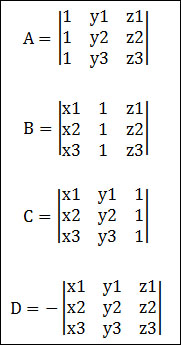
위의 행렬식은 다음과 같이 다시 한번 전개가 됩니다.
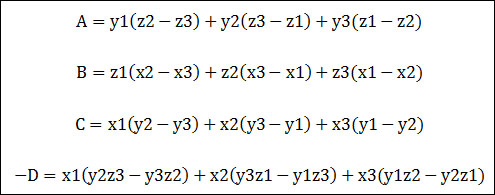
결국 이렇게 구한 A,B,C,D로부터 평면의 방정식이 결정되게 됩니다.

감사합니다, 내용은 요약이지만, 저에겐 매우 유용합니다.
네~ 저두 감사합니다~ ^^
정말 감사합니다. 많은 도움이 되었습니다.
도움되셨다니 다행이구요, 댓글 감사드립니다~ ^^
우와 이거 혼자알아내신거에요? 처음보는거라 신기해요 ㅎ 감사해요
책이나 인터넷에 올라온 자료를 정리한 내용에 불과합니다~ ^^ 댓글 감사드리구요~ 들려주세요~
방향이 바뀌었네요 ^^ ABCD 값 부호 반대 ^^
네 개가 모두 부호가 반대라면 방향이 바뀐게 아니지 않을까요? ABC만 혹은 D만 부호가 달라졌다면 반대 방향이겠지요.
어제 지적하신것을 확인하여, 위의 원문이 틀렸다고 했으나, …
어제 올렸으나, 오늘 다시 확인해보니, 위의 글이 맞습니다. ㅜ_ㅜ 원문 그대로 받아들이시면 됩니다.. 왜 이리 정신이 없을까… 싶네요..
감사합니다.
조만간 써먹어야겠어요~
정말 도움이 되었습니다~
도움되셨다니 좋습니다.
감사합니다 도움이되었습니다.
도움이 되셨다니 좋네요! 감사합니다!
평면 방정식 이해하는데 많은 도움이 되었습니다.
좋은 정보 감사합니다.
제 블로그에 요약 내용을 좀 풀어서 설명을 약간 했는데 괜찮은지 모르겠네요.
(http://blog.daum.net/aero2k/62)
안녕하세요, 매우 정리가 잘된 블로그를 운영하고 계시는군요. ^^
너무 감사드립니다!