하나의 평면에 대해서 2가지의 평면공식이 도출되는데, 이 2가지 평면의 공식에 대해서.. 선과 평면에 대한 교차점을 구하는 방법에 대해서 논의해 보겠습니다. 이 자료는 1991년에 작성된 Paul Bourke(http://local.wasp.uwa.edu.au)님의 글을 좀더 알기 쉽게 풀어 쓴 글입니다.
 방법 1.
방법 1.
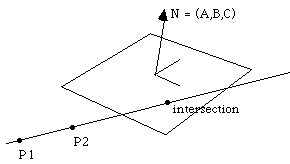
점 P는 평면 위의 임이의 점이고, N은 법선벡터이며 P3는 이미 알고 있는 평면상의 점이라고 하면 평면의 공식은 우리가 고등학교때 배운 평면의 방정식의 형태인, 다음처럼 기술됩니다.
![]()
평면을 수학적으로 기술했으니, 이제는 선에 대한 공식을 알아볼 차례입니다. 이제 앞에서 언급한 점 P를 평면과 선과의 교차점이라고 하면, 점 P는 선에 대한 점입니다. 그리고 선이 지나는 이미 알고 있는 2개의 점을 각각 P1, P2라고 하면 선에 대한 공식은 수학적으로 다음과 같습니다.
![]()
위에서 u는 선에 대한 기울기 값이 되겠지요. 이제.. 평면의 공식에서 P에 선의 공식을 대입할 수 있는 형태입니다. 대입해 보면 아래와 같습니다.
![]()
위의 식을 u에 대해서 전개해 보면 아래와 같은 공식이 됩니다.
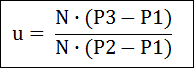
이제 u값을 구했으니.. 이 u값을 선에 대한 공식에 대입하여 교차점 P를 구할 수 있습니다. 다음은 주의할 점입니다.
- 만약 u에 대한 식에서 분모가 0이면, 주어진 선과 평면의 법선은 수직이라는 의미입니다. 즉, 이말은 평면과 선은 서로 만나지 않는다는 의미입니다.
- 교점 P가 P1과 P2 사이에 있는지 검사해야한다면, u값이 0~1사이의 값인지 확인해 보면 됩니다.
방법 2.
이제 평면에 대한 공식으로, 고등학교때 배운 또 다른 형태는 다음과 같습니다.
![]()
(x,y,z)는 평면상의 점이고 (A,B,C)는 평면에 대한 법선벡터이며 D는 이 법선벡터의 길이값입니다. 이 형태의 평면방정식은 임이의 점에 대해서 위의 공식에 대입하여 그 값이 양수인경우 평면을 경계로 법선벡터가 향하는 부분에 존재하는 것이고, 음수인경우는 그 반대방향에 존재하는 것을 간단히 판단할 수 있습니다.
P1(x1,y1,z1)과 P2(x2,y2,z2)를 지나는 선에 대한 공식을 방법1에서의 선에 대한 공식… 다시 언급해 보면 아래와 같습니다.
![]()
위의 선 공식을 방법2에서의 평면의 공식에 대입해 보면 다음과 같은 형태로 전개됩니다.
![]()
위의 식을 u에 대해서 정리해 보면…
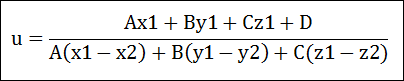
이제 u를 구했으니, 방법1과 마찬가지로 교점을 구할 수 있습니다. 이 방법에 대해 주의할 점은 방법 1과 동일합니다.

기말고사 공부하면서 검색해서 왔는데요
정말 정리 잘 해놓으셨네요 보고 나니깐 평명 방정식이 왜 있는지 이제야 알겠네요 ㅎㅎ 감사.
필레몬님, 시험 기간이군요? 도움이 되셨다니 좋습니다.
시험 잘 보시고, 좋은 결과 있으시면 좋겠습니다.
감사합니다~
아니 어떻게 이렇게 깔끔하게 정리하시나요.. 대단하십니다.
독학 중인데 많은 도움 얻고 갑니다. 정말 감사합니다.
u는 임의의 실수가 되지 않나요?