이 글은 텐서플로나 파이토치와 같은 같은 딥러닝 라이브러리의 기반을 이해하거나, 직접 개발하고자 할때 참고할 만한 글로 작성한 코드는 이해를 위해 나이브하게 작성했다 . 아래는 이 글에서 사용할 모델로 단순화를 위해 은닉층은 없고 입력층과 출력층만이 존재한다.
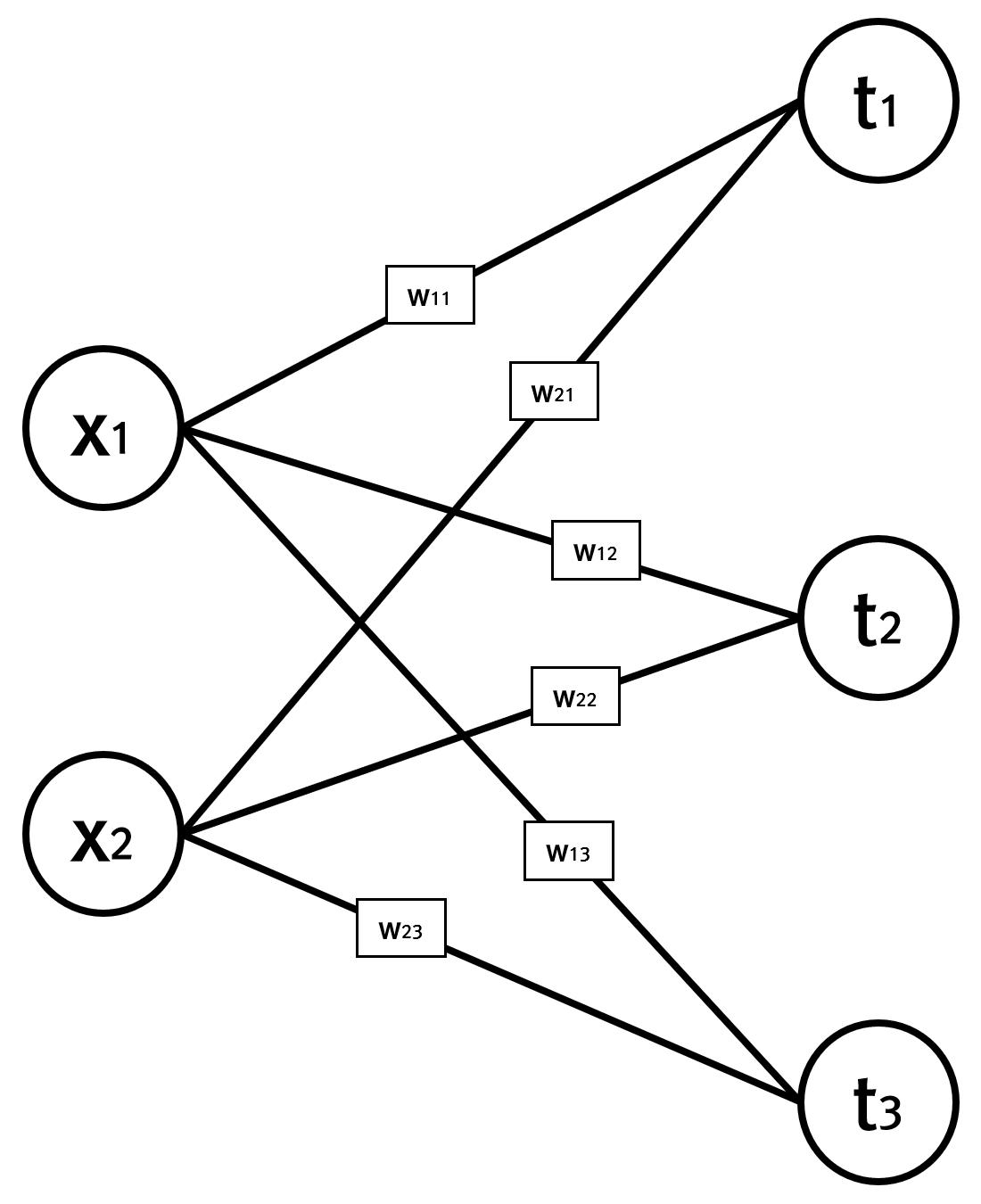
입력값 x와 해당 입력값에 대한 라벨값 t는 다음과 같다.
x = np.array([20.1, 32.2]) t = np.array([0, 0, 1])
데이터가 단일 항목인데, 실제는 그 개수가 상당이 많을 것이다. 가중치 W는 입력값의 특성개수가 2개이고 츨력값의 분류수가 3개이므로 2×3 행렬이며, 초기값은 아래처럼 난수로 잡는다.
W = np.random.randn(2, 3)
모델에 대한 입력 데이터가 정해졌으므로, 초기에 난수로 정한 가중치값을 보정하기 위한 방법인 경사하강법에 대한 함수인 gradient를 다음처럼 사용할 수 있다.
dW = gradient(x, t, W) print(dW)
gradient 함수는 인자로 입력값과 라벨값 그리고 보정할 가중치값이 저장된 행렬을 받으며, 가중치값들을 보정할 경사도(미분값)를 가중치 행렬과 동일한 크기로 반환한다. 먼저 손실함수 loss는 다음과 같다.
def predict(input, weight):
return np.dot(input, weight)
def softmax(input):
input = input - np.max(input)
return np.exp(input) / np.sum(np.exp(input))
def cee(activated, label):
label = label.argmax(axis=0)
result = -np.sum(np.log(activated[label] + 1e-7))
return result
def loss(input, label, weight):
output = predict(input, weight)
activated = softmax(output)
loss = cee(activated, label)
return loss
손실함수는 교차 엔트로피 오차(Cross Entropy Error, CEE) 함수를 사용했으며, 출력층에 대한 활성화 함수는 Softmax를 사용한 것을 알 수 있다. 이제 gradient 함수는 아래와 같다.
def gradient(input, label, weight):
h = 1e-4
grad = np.zeros_like(weight)
it = np.nditer(weight, flags=['multi_index'])
while not it.finished:
idx = it.multi_index
v = weight[idx]
weight[idx] = v + h
fxh1 = loss(input, label, weight)
weight[idx] = v - h
fxh2 = loss(input, label, weight)
grad[idx] = (fxh1 - fxh2) / (2*h)
weight[idx] = v
it.iternext()
return grad
가중치에 대한 W의 각 요소별로 편미분을 기울기 방향을 구하고 있다. 이 기울기 방향으로 일정한 길이만큼 가중치값을 이동해 주는 것을 반복하면 최소의 손실값을 갖는 가중치들의 모음을 얻을 수 있게 된다. 기울기 방향을 구하기 위한 방법으로 편미분에 대한 수치해석 기법을 활용했으나, 실제 텐서플로우나 파이토치 등과 같은 머신러닝 라이브러리에서는 역전파기법을 활용한다.
