활성화 함수(Activation Function)

활성화함수는 입력값이 특정 뉴런에서 처리되어 결과값을 생성할때 적용되는 함수입니다. 활성화 함수로 이 글에서는 3가지를 언급하는데 첫째는 계단함수, 둘째는 시그모이드 함수, 셋째는 ReLU 함수입니다. 각 활성화 함수의 수식과 그래프를 살펴보면 다음과 같습니다.

시그모이드 함수(Sigmoid Function)

$h(x)=\frac{1}{1+e^{-x}}$

위의 식을 그래프로 시각화하기 위한 코드는 아래와 같습니다.

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-10.0, 10, 0.1)
y = sigmoid(x)

plt.plot(x, y)
plt.show()

결과 그래프는 아래와 같습니다.

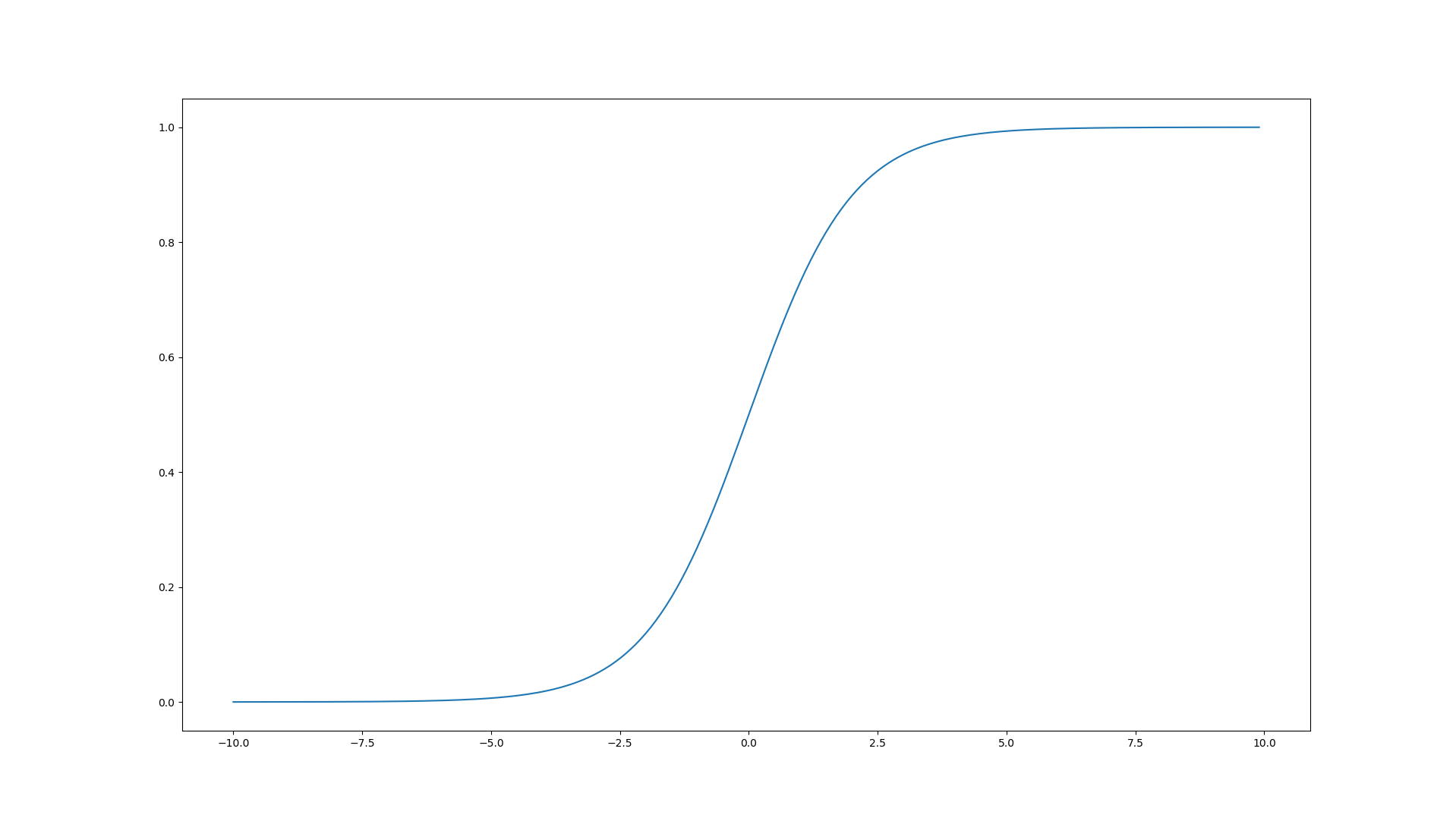
계단함수(Step Function)

$h(x)=\begin{cases} 0 & \quad (x \leq 0)\\ 1 & \quad (x > 0) \end{cases}$

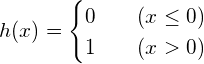
위의 식을 그래프로 시각화하기 위한 코드는 아래와 같습니다.

import numpy as np
import matplotlib.pylab as plt

def step(x):
    return np.array(x > 0, dtype=np.int)

x = np.arange(-10.0, 10, 0.1)
y = step(x)

plt.plot(x, y)
plt.show()

결과 그래프는 아래와 같습니다.

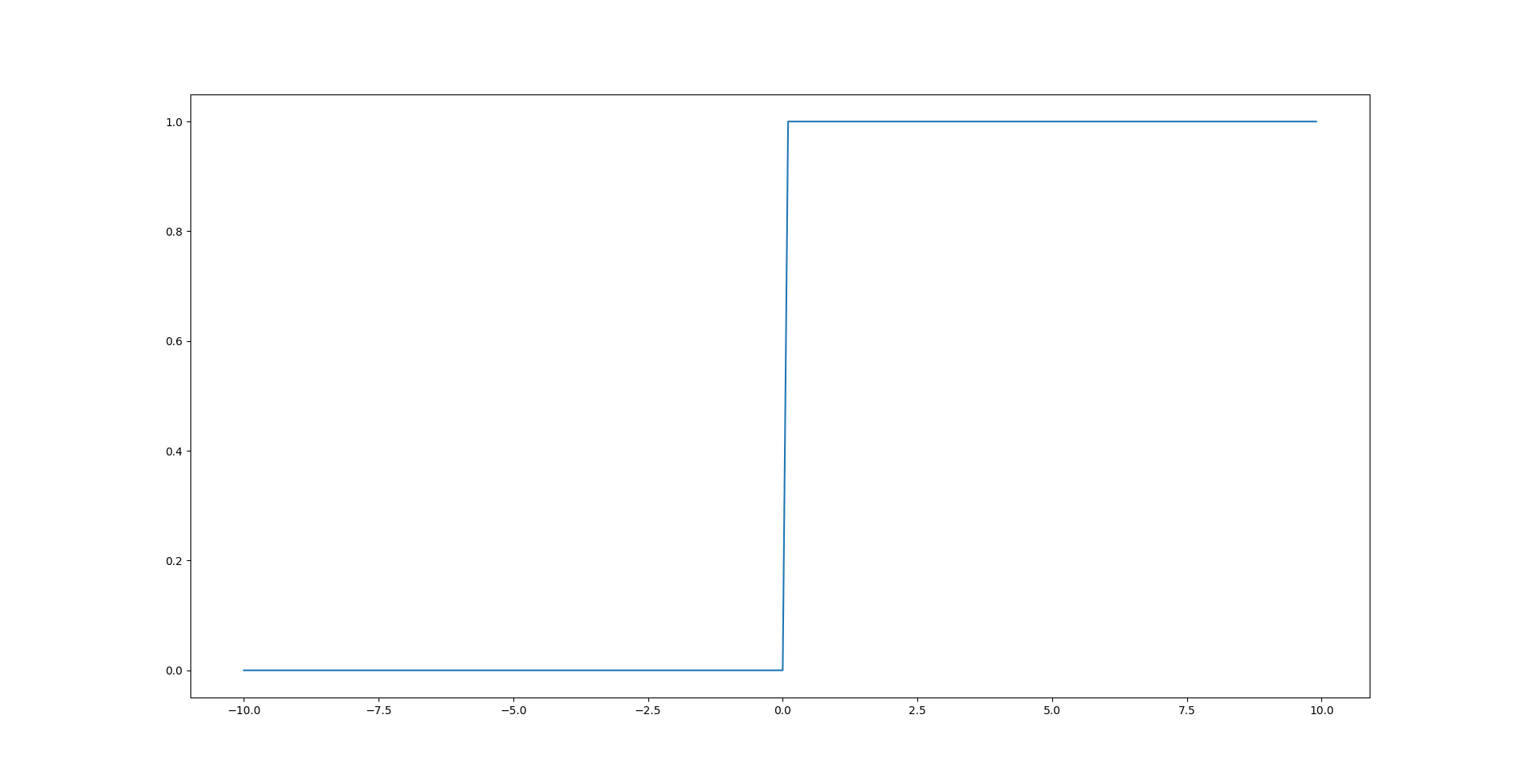
ReLU

$h(x)=\begin{cases} 0 & \quad (x \leq 0)\\ x & \quad (x > 0) \end{cases}$

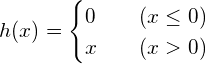
위의 식을 그래프로 시각화하기 위한 코드는 아래와 같습니다.

import numpy as np
import matplotlib.pylab as plt

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-10.0, 10, 0.1)
y = ReLU(x)

plt.plot(x, y)
plt.show()

결과 그래프는 아래와 같습니다.

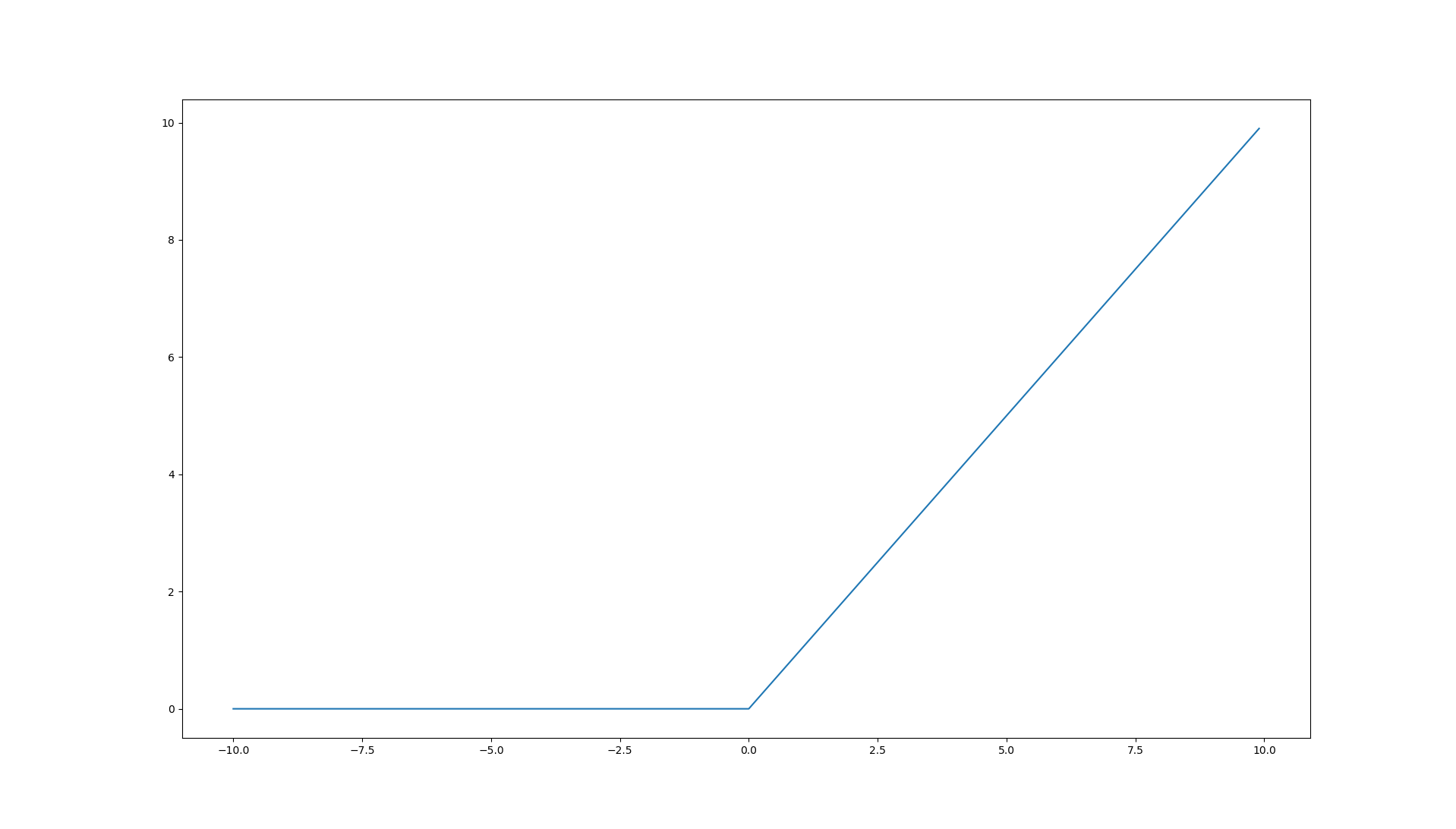
Softmax

모델의 마지막 구성인 출력층에서 입력 데이터가 어떤 클래스로 분류되는지에 대한 확률값으로써 사용되는 활성화 함수로 식은 다음과 같습니다.

$y_{k}=\frac{\exp(a_{k})}{\displaystyle\sum_{i=1}^{n} {\exp(a_{i})}}$

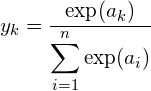
결과적으로 각 출력값들의 합은 1로써 각 출력값을 확률로 해석할 수 있습니다.

쌍곡탄젠트(Hyperbolic Tangent)

활성화 함수로 사용되는 신경망은 대표적으로 RNN입니다. RNN은 순환신경망(Recurrent Network Network)입니다. 수식은 아래와 같습니다.

$tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

그래프로 그려보면 다음과 같습니다.

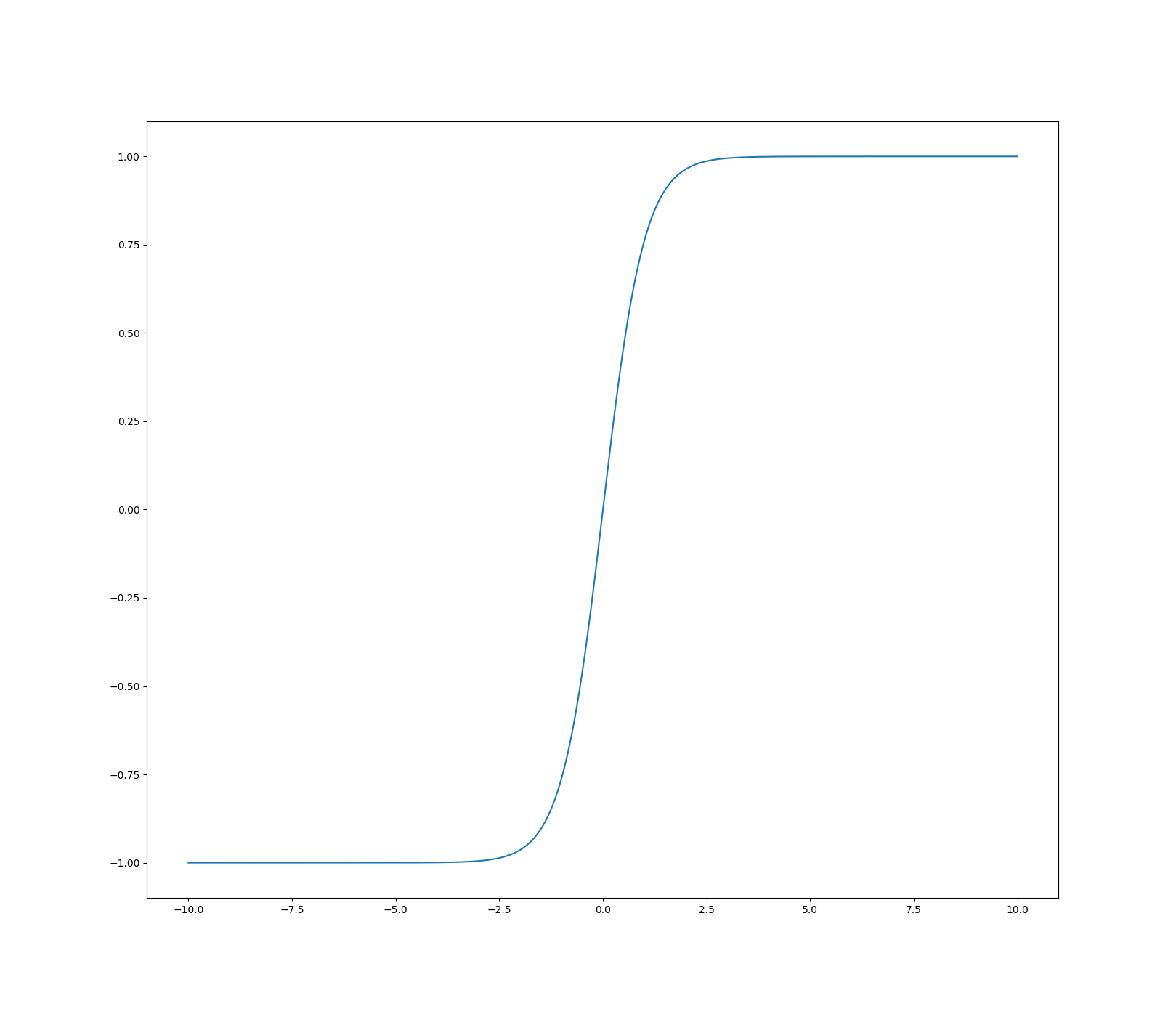
신경망에서의 활성화함수는 각 뉴런계층의 값을 그 다음 뉴런계층으로 전달할때 비선형성을 부여해주게 됩니다. 즉, 활성화함수는 반드시 비선형홤수여야 하며 손실값의 최소화를 위한 경사하강법을 위해 반드시 미분 가능한 함수여야 합니다.

시그모이드 함수(Sigmoid Function)

계단함수(Step Function)

ReLU

Softmax

쌍곡탄젠트(Hyperbolic Tangent)

답글 남기기 응답 취소