수치미분(접선)의 결과를 그래프로 표현하기

다음과 같은 함수가 있을 때.. 이 함수를 미분한 결과는 이 함수의 그래프에 대한 접선의 방정식이 됩니다.

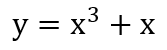
위 함수에 대한 코드 정의는 다음과 같습니다.

def fx(x):
    return x**3 + x

미분은, 중앙차분 방식으로 정의하면 다음과 같구요.

def numerical_diff(f, x):
    h = 1e-4
    return (f(x+h) - f(x-h)) / (2*h)

미분 결과는 접선인데, 이 접선을 표현하는 함수를 반환하는 함수는 다음과 같습니다.

def tangent_line(f, x):
    d = numerical_diff(f, x)
    y = f(x) - d*x
    return lambda t: d*t + y

이제 x 절편의 범위를 0~20까지 잡고 함수의 그래프와 이 함수의 x = 11에서의 접선을 그리는 코드는 다음과 같습니다.

import numpy as np
import matplotlib.pylab as plt

# def numerical_diff(f, x):
# def tangent_line(f, x):
# def fx(x):

x = np.arange(0.0, 20.0, 0.1)
y = fx(x)
plt.plot(x,y)

tf = tangent_line(fx, 11)
y2 = tf(x)
plt.plot(x, y2)

plt.show()

결과 그래프는 다음과 같습니다.

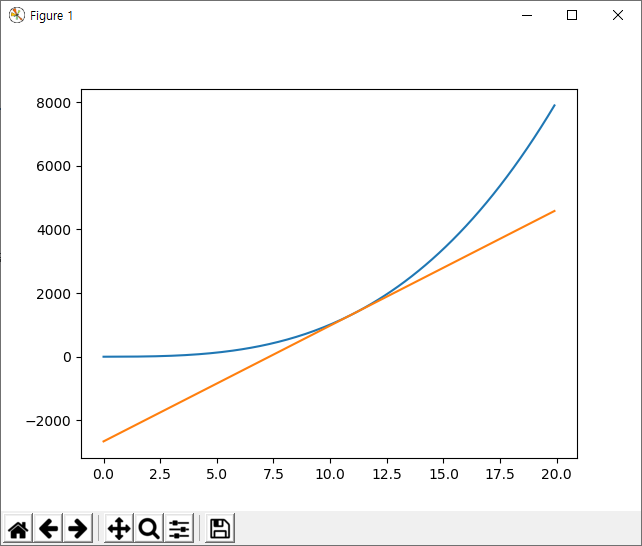
이와 같은 미분에 대한 파이선 코드는 기계 학습이나 신경망 학습에서 가중치와 편향에 대한 최적의 값을 얻기 위해 활용되는 경사하강법(Gradient Descent Method)에서 사용됩니다.

답글 남기기 응답 취소