선과 점 사이의 최소 거리 구하기

원문은 http://local.wasp.uwa.edu.au/~pbourke/geometry/pointline/ 입니다.

지금 진행하고 있는 프로젝트에서 필요한 알고리즘인데, 어디 이미 구현된 소스 코드 없나… 찾다가 발견한것입니다. 찾고보니, 무척 오래전에 봤던 글이네요. 그런데 그때는 소스 코드를 제공하지 않았는데… 여하튼, 다시 복습하는 겸해서 번역해 올립니다. 예전과 다르게 그림도 깔끔해서 그 그림을 그대로 올리겠습니다. 물론 변역이기는 하지만, 나름대로 내용을 보충해서 올렸습니다. 내용 시작합니다~

P1(x1, y1)과 P2(x2, y2)를 지나는 선분의 공식은 아래와 같다.

P = P1 + u(P2 – P1)

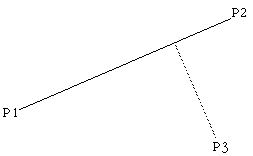
점 P3(x3, y3)는 P1과 P2를 지나는 선분에 인접한 점이다. P3를 선분까지 수직으로 연장한 길이가 바로 우리가 구하고자 하는 값, 즉 최소 거리이다. 수직으로 연장해서 만나는 점을 P라고 하자. 즉, P는 선분 상의 점이 되겠다. 그렇다면, 벡터P3->P와 벡터 P2->P1를 정의할 수 있을 것이고, 이 두 벡터의 내적(Dot Product)는 0이다.

(P3 – P) dot (P2 – P1) = 0

위의 식의 P에 처음에 언급한 선분의 식(P에 대한)을 대입해보면…

[P3 – P1 – u(P2 – P1)] dot (P2 – P1) = 0

위의 식을 u에 대해서 풀어보면,