Convex-Hull 알고리즘 구현

Convex Hull은 볼록한 껍데기로.. 무수히 많은 포인트를 감싸는 볼록한 영역으로 정의할 수 있습니다. 입력 데이터인 포인트는 SHP 파일로부터 제공받아, 이를 듀라맵에서 그 결과를 표시하도록 하였습니다. 아래는 그 결과 화면입니다.

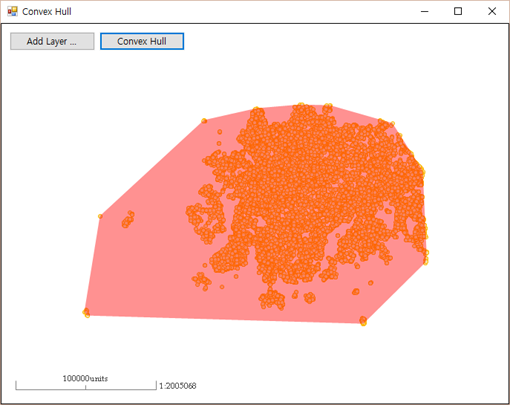
무수히 많은 작은 포인트를 감싸는 Convex Hull이 반투명한 빨간색 폴리곤으로 표시되어져 있습니다. 이러한 Convex-Hull에 대한 구현에 대해 C# 클래스로 정의했으며 아래와 같습니다.

using System;
using System.Collections.Generic;

namespace tstConvexHull
{
    public class ConvexHull
    {
        public class Point : IComparer
        {
            public double x;
            public double y;

            public Point()
            {
                x = 0.0;
                y = 0.0;
            }

            public Point(double x, double y)
            {
                this.x = x;
                this.y = y;
            }

            public int Compare(Point p1, Point p2)
            {
                if (p1.x == p2.x)
                {
                    return p1.y > p2.y ? 1 : p1.y < p2.y ? -1 : 0;
                }
                else
                {
                    return p1.x > p2.x ? 1 : p1.x < p2.x ? -1 : 0;
                }
            }
        }

        public static double Cross(Point O, Point A, Point B)
        {
            return (A.x - O.x) * (B.y - O.y) - (A.y - O.y) * (B.x - O.x);
        }

        public static Point[] Get(Point[] P)
        {
            if (P.Length > 1)
            {
                int n = P.Length, k = 0;
                Point[] H = new Point[2 * n];

                Array.Sort(P, new Point());

                for (int i = 0; i < n; ++i)
                {
                    while (k >= 2 && Cross(H[k - 2], H[k - 1], P[i]) <= 0)
                        k--;
                    H[k++] = P[i];
                }

                for (int i = n - 2, t = k + 1; i >= 0; i--)
                {
                    while (k >= t && Cross(H[k - 2], H[k - 1], P[i]) <= 0)
                        k--;
                    H[k++] = P[i];
                }

                if (k > 1)
                {
                    Point[] NewH = new Point[k - 1];
                    Array.Copy(H, NewH, k - 1);
                    H = NewH;
                }
                return H;
            }
            else if (P.Length <= 1)
            {
                return P;
            }
            else
            {
                return null;
            }
        }
    }
}

실제 위의 Convex-Hull 클래스에 대한 사용은 아래 코드와 같은데요. DuraMap-Xr에서 SHP 파일로부터 점 데이터를 읽어 입력 데이터를 구성하여 Convex-Hull을 실행하고 그 결과로 반투명 빨간색 폴리곤을 추가하는 코드 모두를 나타내고 있습니다.

XrMapLib.ShapeMapLayer lyr = axXr.Layers.GetLayerAsShapeMap("lyr");
XrMapLib.ShapeTable tbl = lyr.ShapeTable;
int cntRows = tbl.RowCount;

ConvexHull.Point[] pts = new ConvexHull.Point[cntRows];

for(int i=0; i
코드를 살짝 설명하면, 1~15번 코드는 SHP 파일로부터 포인트 데이터를 읽어와 Convex-Hull 알고리즘에 입력할 데이터를 준비하는 것이고, 17번 코드가 바로 Convex-Hull의 실행이며 19번 코드부터는 Convex-Hull의 결과를 그래픽 객체로 가시화시켜주는 코드들입니다.