3차원에서, 광원에 의한 물체 표면의 표현을 위해 표면에 수직인 법선 벡터를 고려하게 됩니다. 쉽게 생각해 보면, 물체를 구성하는 좌표에 대한 모델뷰 행렬(M)을 이용해 법선 벡터를 변환하는 것으로 충분할듯하지만 아래처럼 어파인(Affine) 변환 중 y축에 대한 크기 변환을 수행했을 경우, 법선 벡터를 모델뷰 행렬로 변환하면, 표면 벡터(S)와 법선 벡터(N)이 더 이상 수직이 아님을 쉽게 알 수 있습니다.
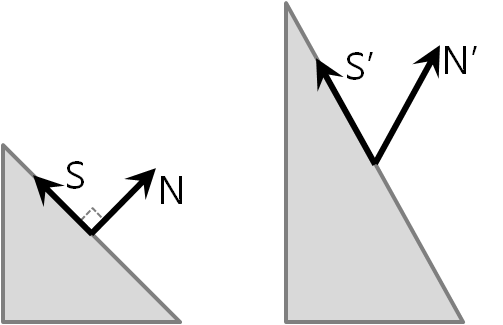
그렇다면 물체에 대해서 어떠한 어파인 변환을 수행하더라도 법선 백터의 고유한 특성, 즉 표면 벡터와 수직인 성질을 유지할 수 있을까하는 것에 대해 정리를 해 봅니다.
먼저 법선 벡터와 표면 벡터는 수직이므로 이 두 벡터의 내적은 0입니다. 즉, 아래와 같습니다.
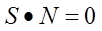
물체는 모델뷰 행렬에 의해 변환됩니다. 즉, 물체의 표면 역시 모델뷰 행렬에 의해 정확히 변환됩니다. 모델뷰 행렬이 M, 표면 벡터를 S, 변환된 표면 벡터를 S’라고 하면 다음과 같습니다.
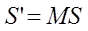
위와 같은 맥락으로, 법선 벡터 N이 법선 벡터로써의 특성을 유지하면서 새롭게 변환된 법선 벡터를 N’라고 할때, 법선 벡터로써의 특성을 유지하면서 변환해 주는 행렬, 즉 법선 행렬을 K라고 하면 다음과 같습니다.
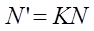
법선 벡터의 특성, 즉 변환된 후의 표면 벡터인 S’와 법선 벡터인 N’는 수직이여야 하므로 다음과 같습니다.
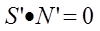
S’=MS 그리고 N’=KN이라고 했으므로 바로 위의 식에 각각 대입하면 다음과 같습니다.
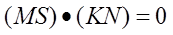
벡터의 기본 성질 중, 벡터의 내적의 결과는 첫번째 벡터의 전치에 의한 벡터의 단순 곱과 같으므로 위의 식은 아래와 같습니다.
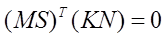
벡터 곱에 대한 전치는 각 벡터의 전치에 대한 역순의 곱과 같으므로 다음의 첫번째 식과 같습니다.
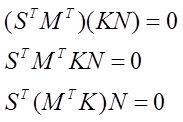
위의 첫째 식은 순차적으로 2번째와 세번째 식으로 변환이 가능합니다. 위의 식중 세번째 식을 “주식”이라고 하겠습니다. S와 N의 내적의 표현은 S의 전치와 N의 곱과 같고, S와 N의 내적의 결과는 0이므로 다음과 같습니다.
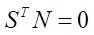
위의 식과 앞서 “주식”이라고 했던 식을 함께 살펴보면, 다음의 결과과 같은 식을 얻을 수 있습니다.
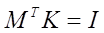
위의 식에서 양변에 M의 전치 행렬에 대한 역행렬을 곱해 주면 최종적으로 K 행렬을 다음처럼 얻을 수 있습니다.
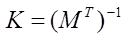
위의 식은 행렬의 기본 성질에 의해 다음과 같습니다.
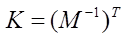
즉, 어떤 변환(M)에 의해 법선 벡터가 그 고유한 특성을 유지할 수 있는 변환을 위한 행렬인 법선행렬은 모델뷰 행렬의 역행렬에 대한 전치 행렬과 같다는 것을 알 수 있습니다.
