가우스 분산(Gauss Distribution) 난수 발생

정규분포(Normal Distribution)이라고도 하는 이 정규분산을 이루는 난수 발생의 필요는 어떤 폴리곤 안에 무작위로 점을 찍어야할 경우에서이다.

처음의 접근은 단순히 폴리곤 안의 점을 무작위로 발생시켜 찍었으나, 폴리곤 안의 점들이 너무 고르게 분포되어져 있다는 문제점이 있었다. 폴리곤의 중심으로 점들이 몰리도록하는 방법이 무엇을까 생각해보니, 가우스분산을 이루도록 점들이 폴리곤안에 난수로 발생시키도록 하였다.

가우스분산을 이루는 난수발생…. 가우스분산이라는 정의를 곰곰이 들여다보면, 어떤 구간에서 그 구간의 중심점에 더 많은 빈도(가중치)가 몰린다는 것이다. 그렇다면 몇번의 난수를 발생시켜 그 평균을 구한다면, 그 값이 가우스분산을 이루는 난수가 아니겠는가?

아래는 이러한 생각에 의한 실제 구현된 코드이다.

double gaussDistributeRand(double begin, double end, size_t detail=5) {
    double r = 0;
    for(size_t i=0; i

인자 detail은 난수를 몇번 발생시켜 평균을 구할 것인가에 대한 것으로 이 값이 커질수록 난수발생값이 중심(평균)으로 집중하는 강도를 나타낸다.

실제로 위의 코드를 적용해서 detail을 1(가우스분산이 아닌 그냥 난수발생), 2, 4, 8, 20, 100으로 주었을때의 실행결과를 보면 아래와 같다.

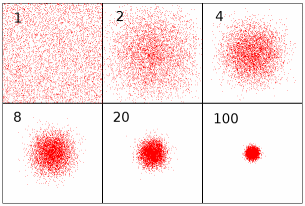
이미 언급한것과 같이 결과에서도 알수있듯 detail값이 커질 수록 중심으로 난수발생값이 집중된다는 것을 알 수 있다.