분석의 핵심은 시각화다.

먼저 이 글은 사이토 고키의 세번째 딥러닝 서적인 Deep Learning from Scratch에 대한 내용(p225)의 코드의 변형된 내용을 언급하고 있습니다. 이 책은 텐서플로나 파이토치 자체를 구현하기 위한 핵심 내용을 다루고 있습니다. 이 글은 이 책에서 다루는 내용 중 역전파에 대한 시각화를 보여주는 코드를 토대로 어떤 수식에 대한 역전파를 통해 미분값을 계산하는데 수행되는 계산 흐름을 시각화하는 내용이며 시각화에 대한 중요성을 언급합니다.

sin 함수의 미분은 해석적으로 볼 때 cos입니다. 다른 방법으로 테일러 급수를 이용해서도 미분값을 구할 수 있고 코드는 다음과 같습니다.

def my_sin(x, threshold=0.00001):
    y = 0
    for i in range(100000):
        c = (-1) ** i / math.factorial(2 * i + 1)
        c = Variable(np.array(c))
        c.name = "c"
        t = c * x ** (2 * i + 1)
        y = y + t
        if abs(t.data) < threshold:
            break
    return y

위의 sin 값을 얻기 위한 함수를 실행하고, 미분값을 얻기 위한 코드는 다음과 같습니다.

x = Variable(np.array(np.pi/4), "x")  
y = my_sin(x)
y.name = "y"
y.backward()

print(y.data)
print(x.grad)

plot_dot_graph(y, verbose=False, to_file="diagram.svg")

위의 코드가 실행되면 PI/4에 대한 sin 값과 PI/4에 대한 sin 미분값이 얻어집니다. 그리고 미분값을 얻기 위해 계산된 처리 과정이 다음처럼 diagram.svg으로 시각화됩니다.

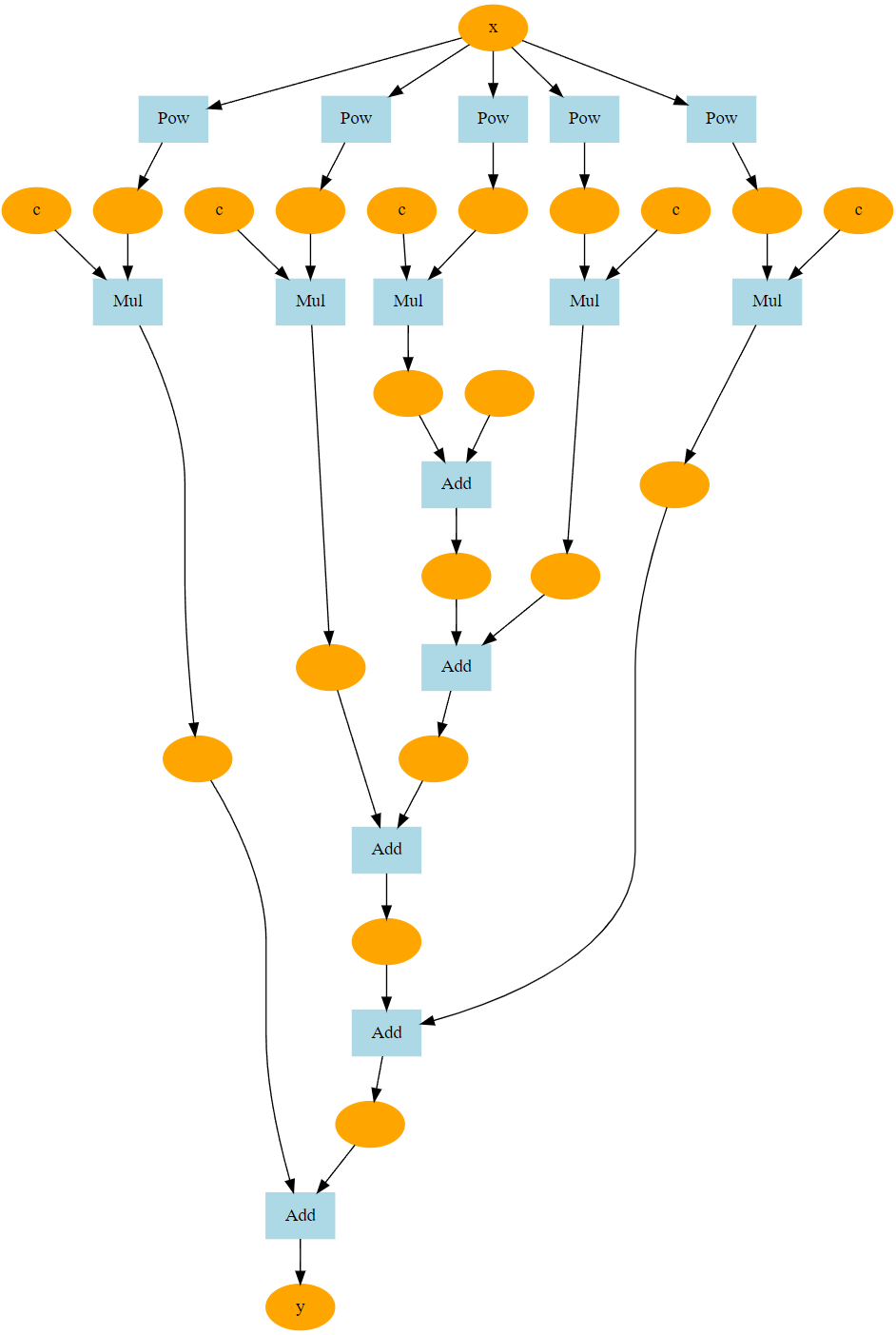
테일러 급수를 통한 sin 값을 얻기 위한 실제 계산의 흐름은 위의 시각화를 통해 좀 더 이해할 수 있습니다.

시각화는 이처럼 무언가를 좀 더 이해하고, 이러한 과정을 통해 더 깊고 정확하게 이해할 수 있는 기회를 제공합니다. 또한 이러한 이해를 통해 더 나은 방법을 찾을 수 있는 최적화와 그 다음 단계로 나아갈 수 있는 입구를 마련해 줍니다. 분석은 어떤 복잡한 현상을 보다 쉽게 이해하기 위해 작은 것들로 나눠 풀어 놓는 작업이라고 할 때 분석에서 매우 중요한 핵심 도구는 시각화입니다. 시각화가 되지 못한 분석은 타인을 이해 시키기도 힘들 뿐더러 과연 그 분석이 정확히 이뤄졌는지도 확인하기 어렵기 때문입니다.

답글 남기기 응답 취소