[GoF] Strategy 패턴

패턴명칭

Strategy

필요한 상황

변경될 가능성이 높은 어떤 알고리즘을 쉽고 효과적으로 교체할 수 있도록 하는 패턴이다.

예제 코드

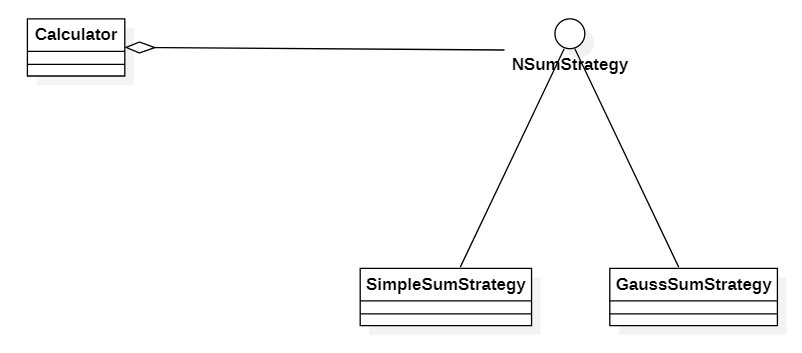
예시를 위해 이 글에서는 변경될 가능성이 높은 알고리즘을 1부터 N까지의 합계를 구하는 것으로 한다. 위의 클래스 다이어그램에서 NSumStrategy는 이 알고리즘의 연산 결과를 얻기 위한 인터페이스만을 정의하는 인터페이스이며 Strategy 패턴의 핵심이다. 코드는 아래와 같다.

package pattern;

public interface NSumStrategy {
	long sum(long N);
}

Calculator 클래스는 어떤 복잡한 연산을 수행하는 기능을 하는데, 복잡한 연산 속에 1부터 N까지 합계를 내는 연산이 필요하다. 코드는 아래와 같다.

package pattern;

public class Calculator {
	private NSumStrategy strategy;
	
	public Calculator(NSumStrategy strategy) {
		this.strategy = strategy;
	}
	
	public double run(int N) {
		return Math.log(strategy.sum(N));	
	}
}

이제 1부터 N까지 합계를 내는 연산에 대한 구체적인 클래스를 정의해보자. 먼저 SimpleSumStrategy 클래스는 다음과 같다. 가장 흔하게 사용되며 매우 직관적인 코드이지만, 반복문을 사용함으로써 수행속도는 느린 방법이다.

package pattern;

public class SimpleNSumStrategy implements NSumStrategy {
	@Override
	public long sum(long N) {
		long sum = N;
		
		for(long i=1; i<N; i++) {
			sum += i;
		}
		
		return sum;
	}
}

다음은 가우스 방식을 사용하는 GaussSumStrategy 클래스이다. 반복문을 사용하지 않아 매우 속도가 빠르다.

package pattern;

public class GaussSumStrategy implements NSumStrategy {
	@Override
	public long sum(long N) {
		return (N+1)*N/2;
	}
}

아래는 실제 1부터 N까지의 합을 필요로 하는 복잡한 연산을 실제로 수행하는 코드이다.

package pattern;

public class Main {
	public static void main(String[] args) {
		Calculator cal1 = new Calculator(new SimpleNSumStrategy()); 
		Calculator cal2 = new Calculator(new GaussSumStrategy());
		
		double result1 = cal1.run(10000000);
		double result2 = cal2.run(10000000);
		
		System.out.println(result1 + " " + result2);
		
	}
}

복잡한 연산 중 일부분인 1부터 N까지의 합을 구하는 방식을 분리하여 쉽게 교체가 가능한 것을 볼 수 있다.