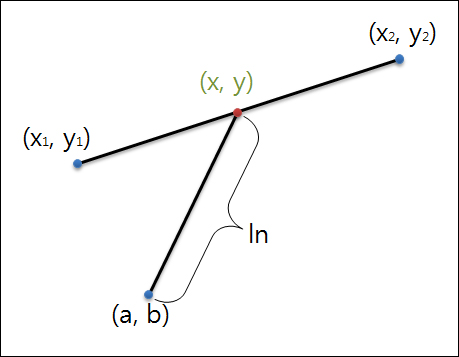
제목이 난해하니 먼저 그림부터 보였습니다. 주어진 선분이 있습니다. 이 선분의 시작점은 (X1, Y1)이고 끝점은 (X2, Y2)입니다. 그리고 주어진 좌표가 있으며 (a, b)입니다. 이 선분과 좌표에 대해서 거리 ln를 가지는 선분상의 좌표를 구하는 것에 대한 정리 포스트입니다. 즉, 위의 그림에서 파란색 점은 주어진 좌표이고 빨간 점을 구하겠다는 것입니다.
먼저 선분에 대한 아래와 같은 매개변수 방정식을 정합니다.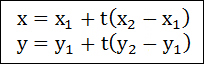
우리가 구해야할 점은 선분상의 점이니 위의 매개변수 방정식에서 x와 y가 바로 우리가 원하는 값입니다. 이 x와 y를 구하기 위해서는 매개변수 t를 구하면 됩니다. 아시겠지만 t가 주어진 선분위에 존재하려면 0~1사이의 값이여야 합니다. 이 값을 벗어나면 답은 없음… 입니다.
이 한가지 관계만 가지고는 않됩니다. 또 하나의 관계를 맺어줘야 합니다. 그 관계는 주어진 좌표(a, b)와 구하고자 하는 선분상의 점(x, y)사이의 거리가 값 ln이라는 사실로부터 다음과 같은 식을 얻을 수 있습니다.![]()
이제 처음 선분에 대한 방정식을 위의 방정식의 x, y에 대입하고 t에 대해 정리를 하면 아래와 같은 t에 대한 2차 방정식이 도출되며 이 2차 방정식을 근의 공식을 통해 t를 구해 보면 다음과 같습니다.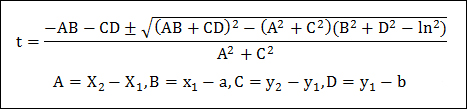
이렇게 구한 t에 대해서 범위가 0~1사이 인지를 검사하고 이 범위에 있다면 이 t를 선분의 방정식에 대입하여 구한 (x, y)가 구하고자 하는 좌표입니다.

공간정보시스템 / 3차원 시각화 / 딥러닝 기반 기술 연구소 @지오서비스(GEOSERVICE)
큰 도움이 되었습니다. ^^;
별 말씀을, ^^ 댓글 감사합니다.
진행하는 프로젝트에 큰 도움이 되었네요. 고맙습니다.
도움이 되었다니 좋습니다.
음.. a, b가 x1과 y1과 같은경우의 공식을 다음과같이 산출했는데요..
그리고 ln 길이값을 알고 있는상태이구요
douT = (douNextPoint(0) – douCurPoint(0)) ^ 2 + ((douNextPoint(1) – douCurPoint(1)) ^ 2) * (douCalLength) ^ 2
douT = Abs(Sqr(douT)) / (douNextPoint(0) – douCurPoint(0)) ^ 2 + (douNextPoint(1) – douCurPoint(1)) ^ 2
douX = douCurPoint(0) + douT * (douNextPoint(0) – douCurPoint(0))
douY = douCurPoint(1) + douT * (douNextPoint(1) – douCurPoint(1))
음.. 제가 잘못 계산한듯한데요..
dounextpoint(0)= x2 : dounextpoint(1) = y2
doucurpoint(0) = x1 : doucurpoint(1) = y1
입니다. 후움.. 공식상으로 맞는건지요???
@_@;;;;; 댓글로 남긴 공식.. 저도 모가 뭔지 저도 모르겠습니다. douT뭐.. dounextpoint 며..