GLSL 예제 : Lighting(광원) – 1/6
원문 : http://www.lighthouse3d.com/opengl/glsl/index.php?lights
OpenGL에는 세가지 종류의 빛이 있습니다: Directional, Point, Spotlight. 이 장에서는 Directional 광원을 구현하는 것으로 시작해 보겠다. 먼저 GLSL을 이용해서 OpenGL의 광원효과를 모방해 보겠다.
우리는 Ambient 빛으로 시작해서 GLSL을 점진적으로 발전시켜 Specular 빛까지 구현해보겠다.
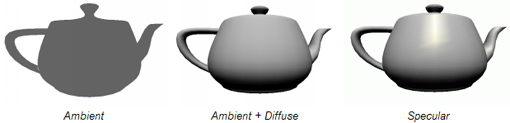
다음으로 좀더 나은 결과를 제공하는 Lighting Per Pixel을 구현해보겠다.
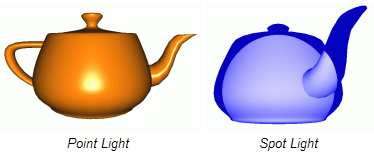
 그리고 이 다음으로는, Point와 Spot Lighting Per Pixel을 구현해보겠다. 빛에 대한 총 6개의 장은 Directional Lights에 관련된 장에서의 코드의 내용을 공통적으로 사용할 것이다.
그리고 이 다음으로는, Point와 Spot Lighting Per Pixel을 구현해보겠다. 빛에 대한 총 6개의 장은 Directional Lights에 관련된 장에서의 코드의 내용을 공통적으로 사용할 것이다.
툰쉐이더에서 언급했듯이, GLSL은 광원 설정에 대한 데이터를 포함하는 OpenGL 상태값에 접근할 수 있다. 이 데이터는 광원 설정에 대한 세세한 내용을 담고 있는 구조체형식의 전역변수이다.
struct gl_LightSourceParameters {
vec4 ambient;
vec4 diffuse;
vec4 specular;
vec4 position;
vec4 halfVector;
vec3 spotDirection;
float spotExponent;
float spotCutoff; // (range: [0.0, 90.0], 180.0)
float spotCosCutoff; // (range: [1.0, 0.0], -1.0)
float constantAttenuation;
float linearAttenuation;
float quadraticAttenuation;
};
uniform gl_LightSourceParameters gl_LightSource[gl_MaxLights];
struct gl_LightModelParameters {
vec4 ambient;
};
uniform gl_LightModelParameters gl_LightModel;재질 속성도 역시 GLSL에서 접근할 수 있다.
struct gl_MaterialParameters {
vec4 emission;
vec4 ambient;
vec4 diffuse;
vec4 specular;
float shiness;
};
uniform gl_MaterialParameters gl_FrontMaterial;
uniform gl_MaterialParameters gl_BackMaterial;광원과 재질에 대한 이 파라메터들의 대부분의 사용은 OpenGL 어플리케이션에서 사용하는 것과 유사하다. 이제 우리는 이들 속성을 사용해서 Directional 광원을 구현해 볼 것이다.

 이전이랑 결과가 똑같네? =_=;; 뭐여….?
이전이랑 결과가 똑같네? =_=;; 뭐여….? 다음 장에서는 쉐이더를 통해 다양한 광원에 대해 살펴보겠다.
다음 장에서는 쉐이더를 통해 다양한 광원에 대해 살펴보겠다.