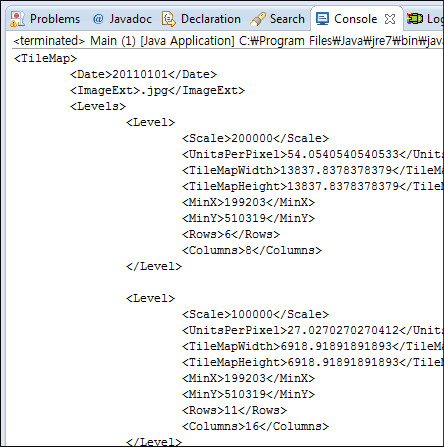
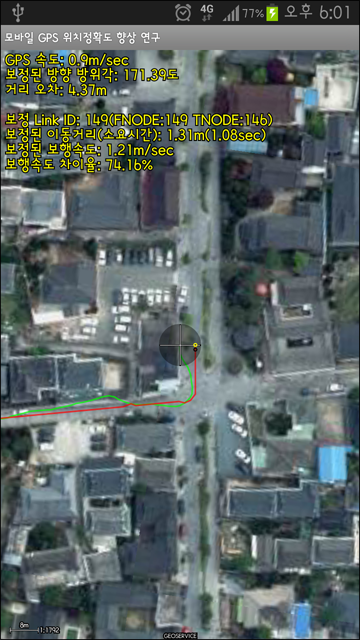
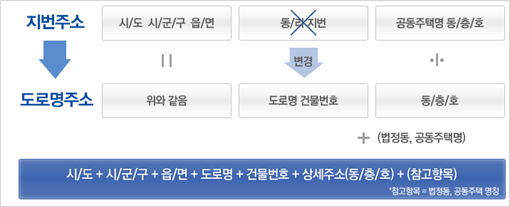
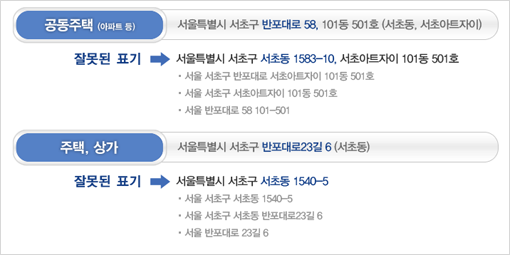
이 책은 구글, 네이버, 다음 등에서 제공하는 지도 API를 사용하지 않고 항공영상이나 수치지도를 활용하여 직접 지도를 디자인하고 제작하여 지도와 관련된 보다 다양한 정보와 데이터를 활용할 수 있고, 더 나아가 공간연산과 분석을 통해 더 고도화된 모바일 GIS 앱 개발을 하는데 큰 도움을 줄 것으로 확신합니다.

http://www.yes24.com/24/goods/8297262?scode=032&OzSrank=1
사용자 저마다의 원하는 다양한 앱을 개발하는 데 필요한 전문 GIS 엔진을 소개하고 이 엔진의 활용방법을 자세한 튜토리얼 형식으로 제공함으로써 독자들이 원하는 모바일 GIS 앱을 쉽고 빠르게 개발할 수 있도록 구성되었습니다.
이 책에서 소개하는 모바일 GIS 엔진은 블랙포인트(BlackPoint-Xr)로 저자가 직접 개발한 엔진이며, 이를 통해 다양한 공간 데이터에 대한 검색 및 편집기능을 수행할 수 있고 더 나아가 공간연산 및 분석을 통한 전문적인 업무까지 지원 가능한 GIS 앱을 개발할 수 있습니다. 또한, GPS를 통한 위치 추적 및 다양한 좌표계 변환을 쉽게 지원하도록 설계되었습니다.
모바일 GIS 앱을 개발하기 위해 이 책에서 소개하는 블랙포인트는 이미 많은 기관에서 현장 중심의 모바일 GIS의 기반 엔진으로 사용되고 있으며 많은 GIS 회사에서 블랙포인트를 이용해 직접 모바일 GIS 앱을 개발함으로써 검증된 모바일 GIS 엔진입니다.
이미 국가에서 다양한 공간데이터를 일반인들이 사용할 수 있도록 공개하고 있으며 그 공개의 범위도 더욱 넓어지리라 생각합니다. 이러한 공간 데이터를 이용하여 자신이 원하는 모바일 GIS 앱을 개발하여 직접 사용한다는 것은 큰 경쟁력이라 생각합니다.
저자 소개
김형준 : 지리정보시스템(GIS) 분야의 개발자이다. 웹 기반의 GIS 엔진과 모바일 GIS 엔진을 개발했으며 현재 HTML5 기반의 GIS 엔진을 개발 중이다. 지도 관련 서비스 개발에 관심이 많으며 많은 개발자가 제약 없이 쉽게 사용할 수 있는 다양한 Open API를 개발하고 있다.
이근상 : 한국수자원공사에서 연구원으로 지냈으며 현재 전주비전대학교의 교수로 재직 중이다. ‘GIS 공간분석’을 전문분야로 연구하고 있으며, 도시계획 및 토지이용 계획을 지원하기 위한 다양한 공간분석 알고리즘 개발을 비롯하여 홍수 및 토양침식과 같은 수재해 관련 공간분석 알고리즘 개발 및 현장 적용 등을 응용분야로 연구하고 있다. 최근에는 모바일 관광업무 지원을 위한 위치 서비스 개선 및 토지정보 현장지원 시스템에 관한 연구도 수행 중이다.
박진호 : 현재 공간정보기술(주) 연구소에서 근무 중이다. 10여 년간 IT와 GIS 관련 분야에 종사하면서 급변하는 IT 기술에 대해 연구하고 있다. 최근에는 1인 1GPS를 가능케 한 스마트폰 확산을 기회로 삼아 최신 IT 기술의 접목을 통한 GIS 산업영역 확대라는 작은 소망의 실현을 위해 노력 중이다.