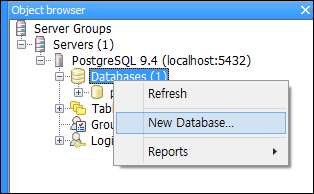
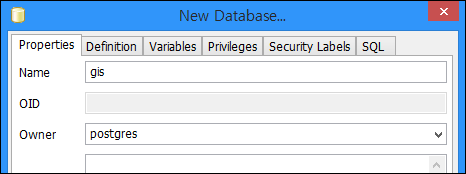
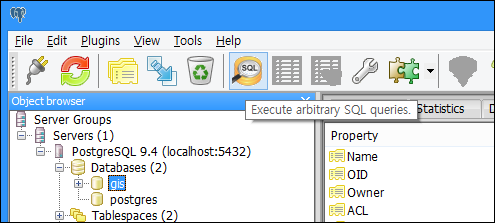
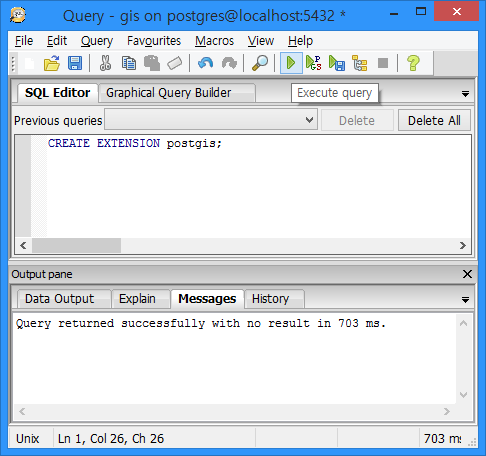
GIS 공간서버인 GeoService-Xr은 JRE를 지원하는 Linux, Unix, Windows 등의 OS에서 구동할 수 있는 서버 프로그램인데요. 사용하기가 쉽고 기능이 단순한만큼 매우 안정적인 공간서버입니다. 안정성에 대한 하나의 예로 119 소방재난본부에서 도입되어 2년 가까이 단 한번도 중단된 적이 없이 운영되고 있습니다.
GeoService-Xr은 Xr 패키지를 구성하는 하나의 요소인데요. Xr 패키지는 공간 서버를 중심으로 웹, 모바일, PC에서 운영할 수 있는 GIS 시스템을 개발할 수 있는 총체적인 솔루션을 제공하며 배경지도와 지오코딩 기능을 제공하니다. 아래는 Xr 솔루션에 대한 소개 PDF와 내용중 GeoService-Xr에 대한 스틸샷입니다.
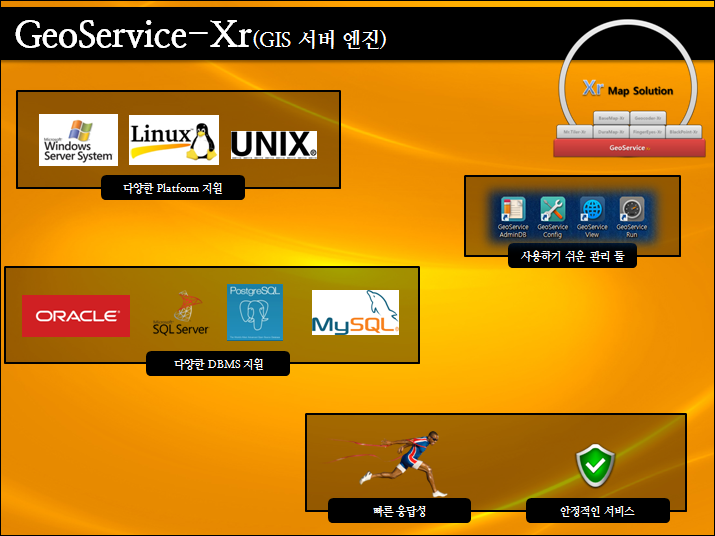
아래는 GeoService-Xr에 대한 사용자 메뉴얼입니다. GUI 관리툴을 제공하고 이 관리툴을 이용해 보다 쉽게 서버를 관리할 수 있습니다. 페이지 수가 표지 포함하여 35페이지인데요. 처음 접하는 사용자도 빠른 시간 내에 제품에 익숙 해지고 바로 프로젝트에 적용할 수 있다는 장점이 있습니다.

(주)지오서비스는 지금까지 자체적으로 개발한 GIS 제품군인 Xr 솔루션을 이용하여 웹, 모바일, 데스크탑에서 운영할 수 있는 GIS 어플리케이션 개발과 공간DB 가공 및 고도화 작업을 해 왔습니다. 향후 더 많은 GIS 어플리케이션 개발과 공간 DB 가공 및 고도화 작업을 통해 실무에 더욱 효과적이면서 적합한 Xr 솔루션으로 발전해 나아갈 것 입니다.