아래와 같은 식을 회귀하는 모델을 구하는 두가지 접근을 PyTorch로 살펴본다.
![]()
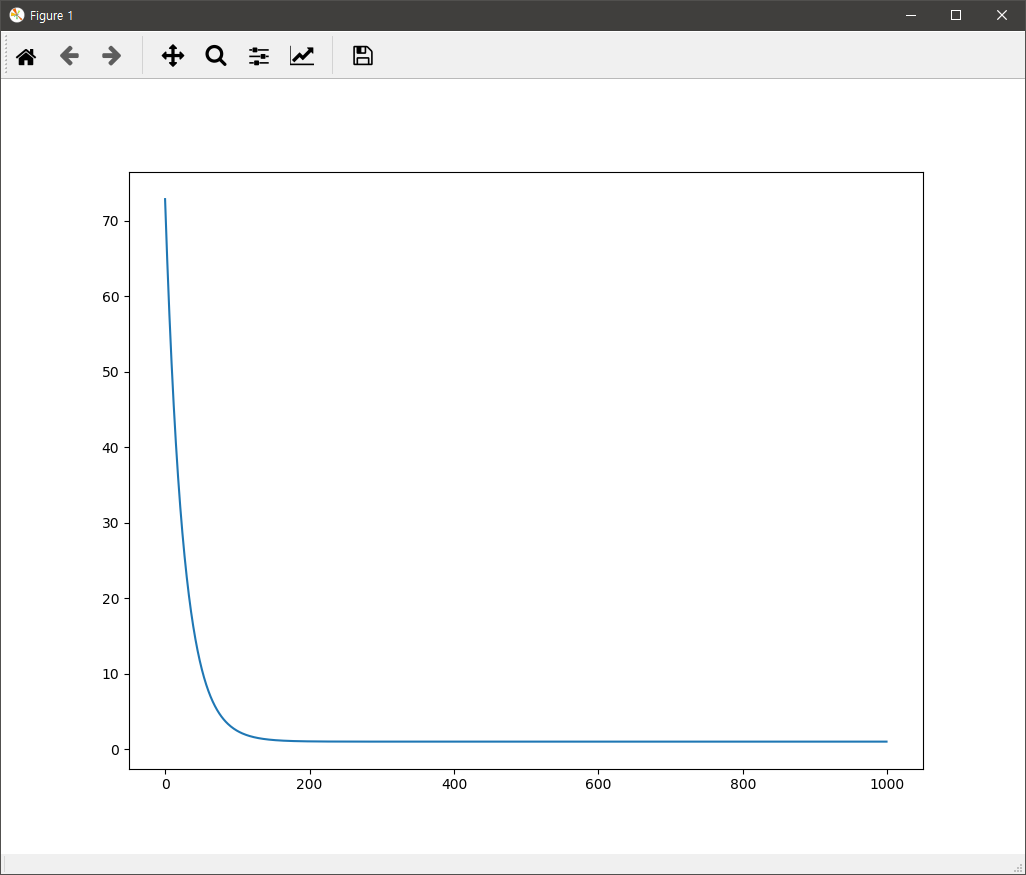
즉, 입력값(a, b)에 대한 출력값 y가 100개 주어지고, 이 데이터를 통해 상수항인 1과 계수 5, 7을 구하는 것이 문제다. 물론 y에는 오차가 반영되어 있다. 첫번째 접근은 다음과 같다. 손실함수는 평균최소제곱을, 역전파를 통한 최적값 수렴을 위한 기울기를 구해 반영한 학습률은 0.01을 사용했다. 아래의 코드의 경우 기울기를 구하기 위한 방법을 PyTorch의 역전파를 이용한 것이다.
import torch
from matplotlib import pyplot as plt
weight_true = torch.Tensor([1,5,7]) # y = 1 + 5a + 7b
X = torch.cat([torch.ones(100,1),torch.randn(100,2)], 1)
y = torch.mv(X, weight_true) + torch.randn(100)
weight = torch.randn(3, requires_grad=True)
lr = 0.01
losses = []
for epoch in range(1000):
weight.grad = None
y_pred = torch.mv(X, weight)
loss = torch.mean((y - y_pred)**2)
loss.backward()
weight.data = weight.data - lr*weight.grad.data
losses.append(loss.item())
print(weight)
plt.plot(losses)
plt.show()
두번째 접근은 다음과 같다. 앞서 직접 하나 하나 개발자가 지정했던 것들에 대한 모듈을 사용한 경우이다.
import torch
from torch import nn, optim
from matplotlib import pyplot as plt
weight_true = torch.Tensor([1,5,7]) # y = 1 + 5a + 7b
X = torch.cat([torch.ones(100,1),torch.randn(100,2)], 1)
y = torch.mv(X, weight_true) + torch.randn(100)
net = nn.Linear(in_features=3, out_features=1, bias=False)
optimizer = optim.SGD(net.parameters(), lr=0.01)
loss_fn = nn.MSELoss()
losses = []
for epoch in range(1000):
optimizer.zero_grad()
y_pred = net(X)
loss = loss_fn(y_pred.view_as(y), y)
loss.backward()
optimizer.step()
losses.append(loss.item())
print(net.weight)
plt.plot(losses)
plt.show()
두 경우 모두 실행하면 아래와 같은 손실값에 대한 그래프와 추론된 상수와 두계수 값이 콘솔에 출력된다.
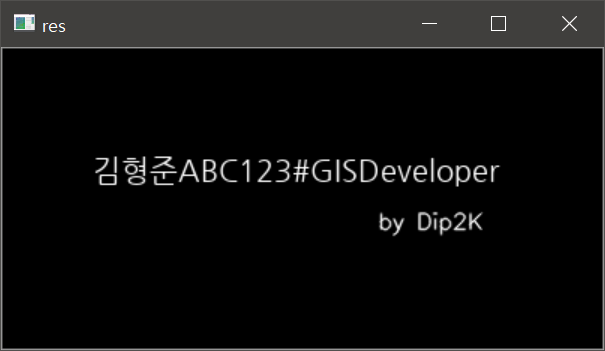
OpenCV의 이미지에 한글 출력하기
사실 OpenCV의 이미지는 numpy의 배열입니다. 그런데 문제는 파이썬에서 OpenCV를 통해 텍스트를 출력할때 한글 출력이 쉽지 않습니다. 해서 한글 출력을 위해 PIL(Python Imaging Library)의 도움을 받을 수 있습니다. 아래의 예제가 바로 그것입니다.
import numpy as np
from PIL import ImageFont, ImageDraw, Image
import cv2
img = np.zeros((200,400,3),np.uint8)
b,g,r,a = 255,255,255,0
fontpath = "fonts/gulim.ttc"
font = ImageFont.truetype(fontpath, 20)
img_pil = Image.fromarray(img)
draw = ImageDraw.Draw(img_pil)
draw.text((60, 70), "김형준ABC123#GISDeveloper", font=font, fill=(b,g,r,a))
img = np.array(img_pil)
cv2.putText(img, "by Dip2K", (250,120), cv2.FONT_HERSHEY_SIMPLEX, 0.5, (b,g,r), 1, cv2.LINE_AA)
cv2.imshow("res", img)
cv2.waitKey()
cv2.destroyAllWindows()
7-12번 코드가 PIL을 이용해 한글을 출력하는 코드이고, 14~15번 코드는 OpenCV의 텍스트 출력 코드입니다. 결과는 다음과 같습니다.
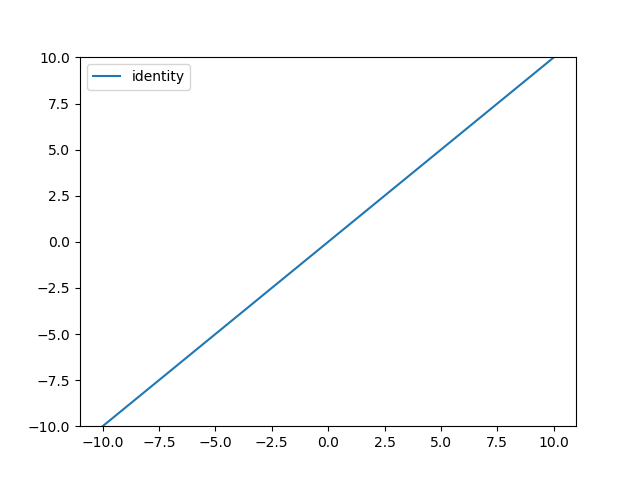
함수들에 대한 그래프 시각화
선형 함수에 대한 정의와 그래프 시각화는 다음 코드와 같다.
import numpy as np
import matplotlib.pylab as plt
def identity_func(x):
return x
x = np.arange(-10, 10, 0.01)
plt.plot(x, identity_func(x), linestyle='-', label="identity")
plt.ylim(-10, 10)
plt.legend()
plt.show()
결과는 다음과 같다.
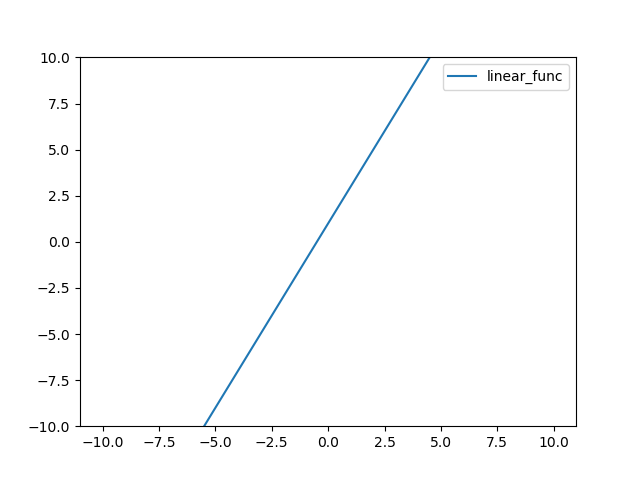
기울기와 y절편을 고려한 선형 함수의 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def linear_func(x):
return 2 * x + 1
x = np.arange(-10, 10, 0.01)
plt.plot(x, linear_func(x), linestyle='-', label="linear_func")
plt.ylim(-10, 10)
plt.legend()
plt.show()
결과는 다음과 같다.
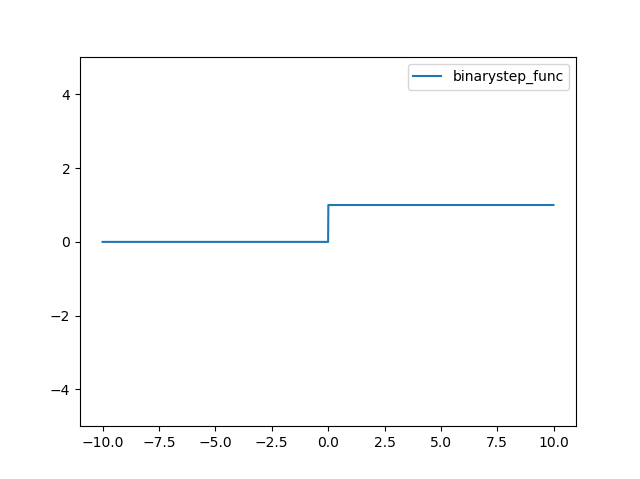
계단함수에 대한 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def binarystep_func(x):
return (x>=0)*1
x = np.arange(-10, 10, 0.01)
plt.plot(x, binarystep_func(x), linestyle='-', label="binarystep_func")
plt.ylim(-5, 5)
plt.legend()
plt.show()
결과는 다음과 같다.
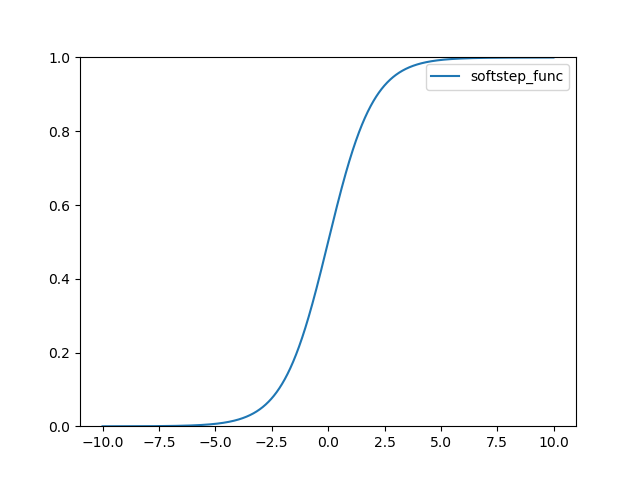
로지스틱(Logistic) 또는 시그모이드(Sigmoid)라고 불리는 함수 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softstep_func(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-10, 10, 0.01)
plt.plot(x, softstep_func(x), linestyle='-', label="softstep_func")
plt.ylim(0, 1)
plt.legend()
plt.show()
결과는 다음과 같다.
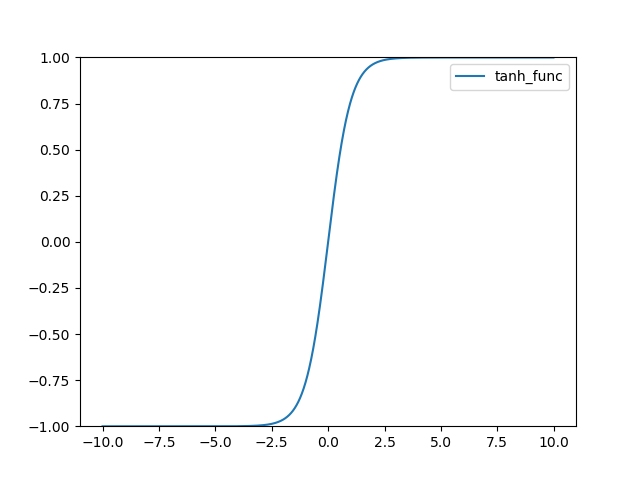
TanH 함수 정의 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def tanh_func(x):
return np.tanh(x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, tanh_func(x), linestyle='-', label="tanh_func")
plt.ylim(-1, 1)
plt.legend()
plt.show()
그래프는 다음과 같다.
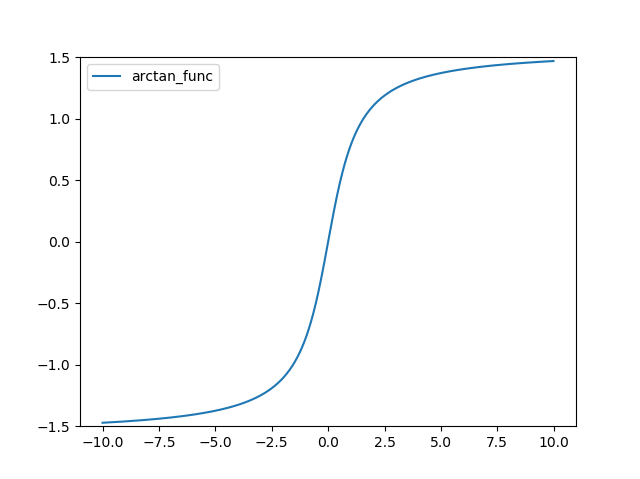
ArcTan 함수 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def arctan_func(x):
return np.arctan(x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, arctan_func(x), linestyle='-', label="arctan_func")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.show()
그래프는 다음과 같다.
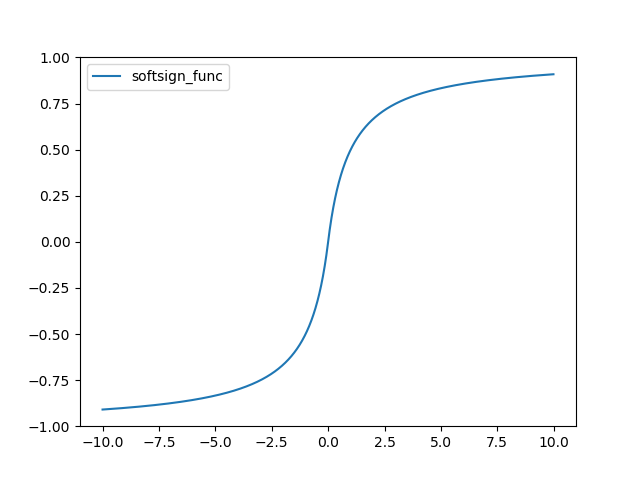
Soft Sign 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softsign_func(x):
return x / ( 1+ np.abs(x) )
x = np.arange(-10, 10, 0.01)
plt.plot(x, softsign_func(x), linestyle='-', label="softsign_func")
plt.ylim(-1, 1)
plt.legend()
plt.show()
그래프는 다음과 같다.
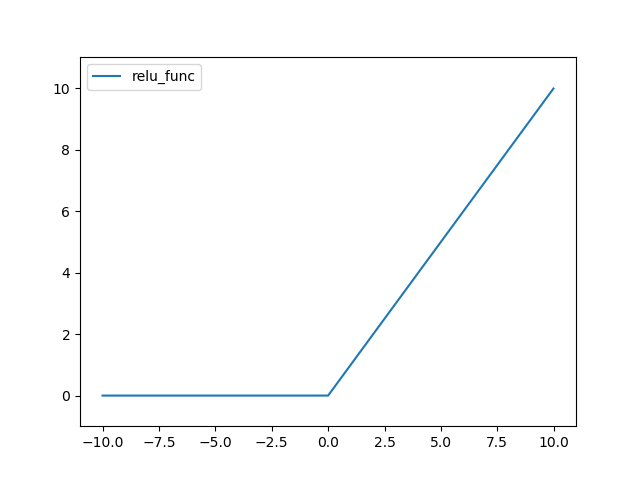
ReLU(Rectified Linear Unit) 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def relu_func(x):
return (x>0)*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, relu_func(x), linestyle='-', label="relu_func")
plt.ylim(-1, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
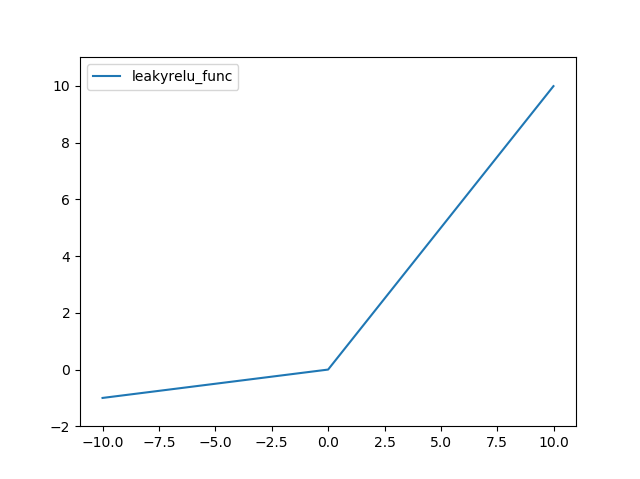
Leaky ReLU 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def leakyrelu_func(x, alpha=0.1):
return (x>=0)*x + (x<0)*alpha*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, leakyrelu_func(x), linestyle='-', label="leakyrelu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
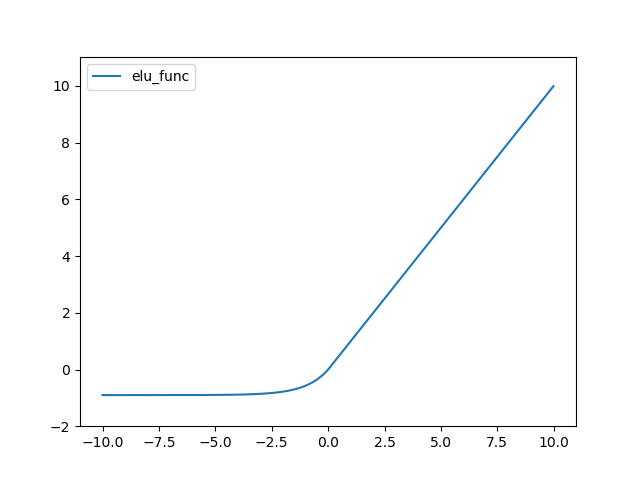
ELU(Exponential Linear Unit) 함수는 다음과 같다.
def elu_func(x, alpha=0.9):
return (x>=0)*x + (x<0)*alpha*(np.exp(x)-1)
x = np.arange(-10, 10, 0.01)
plt.plot(x, elu_func(x), linestyle='-', label="elu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
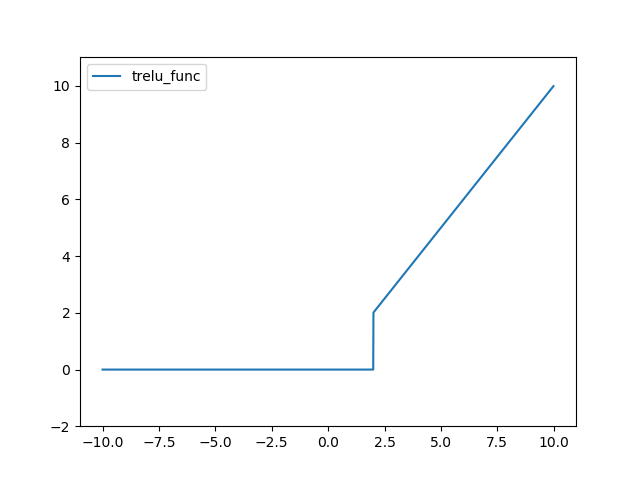
TreLU 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def trelu_func(x, thres=2):
return (x>thres)*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, trelu_func(x), linestyle='-', label="trelu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
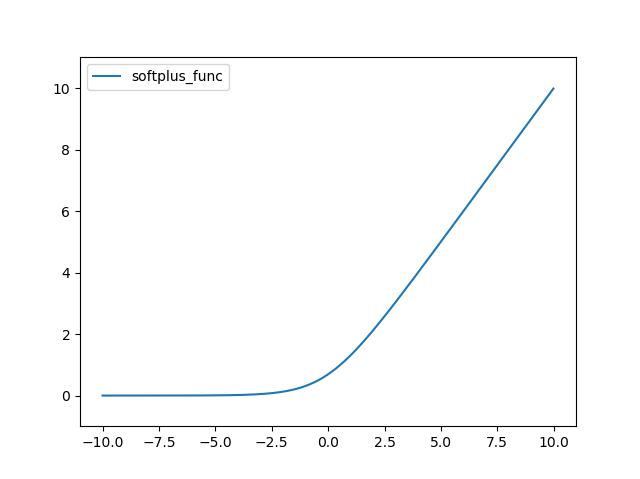
SoftPlus 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softplus_func(x):
return np.log( 1 + np.exp(x) )
x = np.arange(-10, 10, 0.01)
plt.plot(x, softplus_func(x), linestyle='-', label="softplus_func")
plt.ylim(-1, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
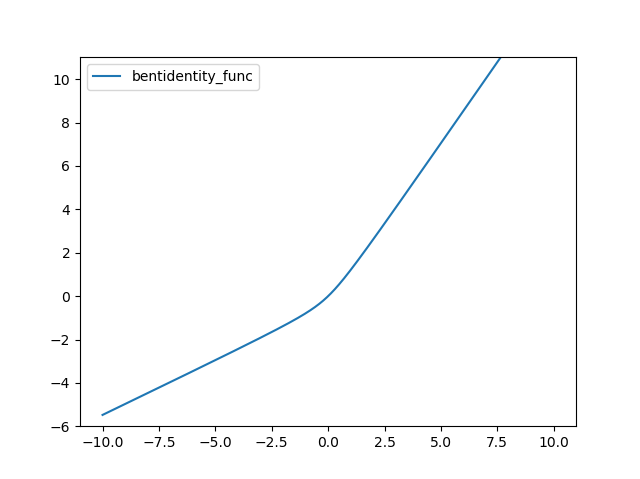
Bent identity 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def bentidentity_func(x):
return (np.sqrt(x*x+1)-1)/2+x
x = np.arange(-10, 10, 0.01)
plt.plot(x, bentidentity_func(x), linestyle='-', label="bentidentity_func")
plt.ylim(-6, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
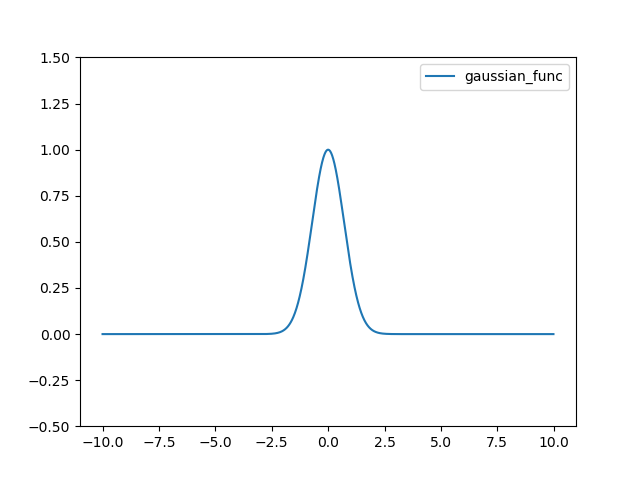
Gaussian 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def gaussian_func(x):
return np.exp(-x*x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, gaussian_func(x), linestyle='-', label="gaussian_func")
plt.ylim(-0.5, 1.5)
plt.legend()
plt.show()
결과는 다음과 같다.
psql을 설치된 서버에서 직접 실행하기
PostgreSQL에 대한 콘솔 관리자는 psql입니다. 현재 CentOS에서 설치해 사용중이고, DB 작업시에는 Telnet을 통해 작업을 해왔는데, 시간을 단축하고자 원격방식이 아닌 직접 서버단에서 작업을 했습니다. 원격 작업시 준비된 SQL에 대한 처리에만 2일정도 소요되는 작업이 10시간정도 소요되었습니다.
이 글은 추후 PostgreSQL이 설치된 서버에서 직접 psql을 실행하고자 할때 입력했던 콘솔 명령을 기록해 둡니다.
먼저 아래처럼 root로 로그인한 상태에서 postgres 계정으로 전환합니다.
sudo -i -u postgres
그리고 psql을 실행합니다. 바로 암호를 묻는데 postgres 계정에 대한 암호를 입력합니다.
기본적으로 psql은 postgres라는 이름의 데이터베이스에 연결됩니다. 이를 내가 원하는 데이터베이스로 연결하고자할 때 아래처럼 입력합니다.
\c database_name_to_be_connected
필요하다면, SQL 문의 인코딩 방식을 변경해줘야 하는데요. 아래처럼 입력하여 원하는 방식으로 변경할 수 있습니다.
set client_encoding = 'UTF8';
이제 준비된 SQL문이 저장된 파일로부터 SQL 문을 실행하기 위해 아래처럼 입력합니다.
\i /somewhere_dir/file_name_to_be_ran
pandas의 DataFrame에 대한 Inner Join, Outer Join, Left Join, Right Join
판다스에서 데이터프레임은 테이블 형식의 데이터셋입니다. DBMS의 Table들 간에도 Join을 맺을 수 있듯이, 마찬가지로 판다스의 데이터프레임들 간에도 Join을 맺을 수 있습니다. 물론 Join을 맺을 공통 필드가 존재한다면 말입니다.
Join에는 모두 4가지 방식이 존재합니다. 즉, 두 데이터셋 간의 중복된 요소만을 Join하는 Inner Join과 두 데이터셋에 대한 모든 데이터를 Join하는 Outter Join, 그리고 왼쪽 데이터셋을 기준으로 하는 Left Join과 오른쪽 데이터셋을 기준으로 하는 Right Join입니다. 보다 명확한 Join의 파악은 아래의 코드 예제를 통해 파악할 수 있습니다.
먼저 Join 하고자 하는 데이터셋으로, 판다스의 데이터프레임을 아래 코드처럼 정의합니다.
import pandas as pd
data_A = {'key': [1,2,3], 'name': ['Jane', 'John', 'Peter']}
dataframe_A = pd.DataFrame(data_A, columns = ['key', 'name'])
data_B = {'key': [2,3,4], 'age': [18, 15, 20]}
dataframe_B = pd.DataFrame(data_B, columns = ['key', 'age'])
print(dataframe_A)
print(dataframe_B)
결과는 아래와 같습니다.
key name 0 1 Jane 1 2 John 2 3 Peter key age 0 2 18 1 3 15 2 4 20
두 데이터프레임 간에는 key라는 공통 필드가 존재하는 것을 볼 수 있습니다. 이를 토대로 먼저 Inner Join에 대한 코드입니다.
df_INNER_JOIN = pd.merge(dataframe_A, dataframe_B, left_on='key', right_on='key', how='inner') print(df_INNER_JOIN)
위의 코드의 결과는 다음과 같습니다.
key name age 0 2 John 18 1 3 Peter 15
다음은 Outer Join에 대한 코드입니다.
df_OUTER_JOIN = pd.merge(dataframe_A, dataframe_B, left_on='key', right_on='key', how='outer') print(df_OUTER_JOIN)
결과는 다음과 같습니다.
key name age 0 1 Jane NaN 1 2 John 18.0 2 3 Peter 15.0 3 4 NaN 20.0
다음은 Left Join에 대한 코드입니다.
df_LEFT_JOIN = pd.merge(dataframe_A, dataframe_B, left_on='key', right_on='key', how='left') print(df_LEFT_JOIN)
결과는 다음과 같습니다.
key name age 0 1 Jane NaN 1 2 John 18.0 2 3 Peter 15.0
다음은 Right Join에 대한 코드입니다.
df_RIGHT_JOIN = pd.merge(dataframe_A, dataframe_B, left_on='key', right_on='key', how='right') print(df_RIGHT_JOIN)
다음은 실행 결과입니다.
key name age 0 2 John 18 1 3 Peter 15 2 4 NaN 20
모든 Join은 pd.merge 함수를 통해 이루어지는데요. 위의 예제 코드를 보면 두 데이터프레임의 Join 필드가 모두 ‘key’라는 것을 알 수 있습니다. 이처럼 Join 필드의 이름이 동일할 경우 pd.merge의 left_on과 right_on 인자 대신 on 인자 하나로 대체가 가능합니다. 예를들어, Inner Join의 경우는 아래와 같습니다.
df_INNER_JOIN = pd.merge(dataframe_A, dataframe_B, on='key')
pd.merge 함수의 인자중 how도 생략되었는데, 이는 Inner Join이 pd.merge의 인자 how의 기본값이기 때문입니다.
