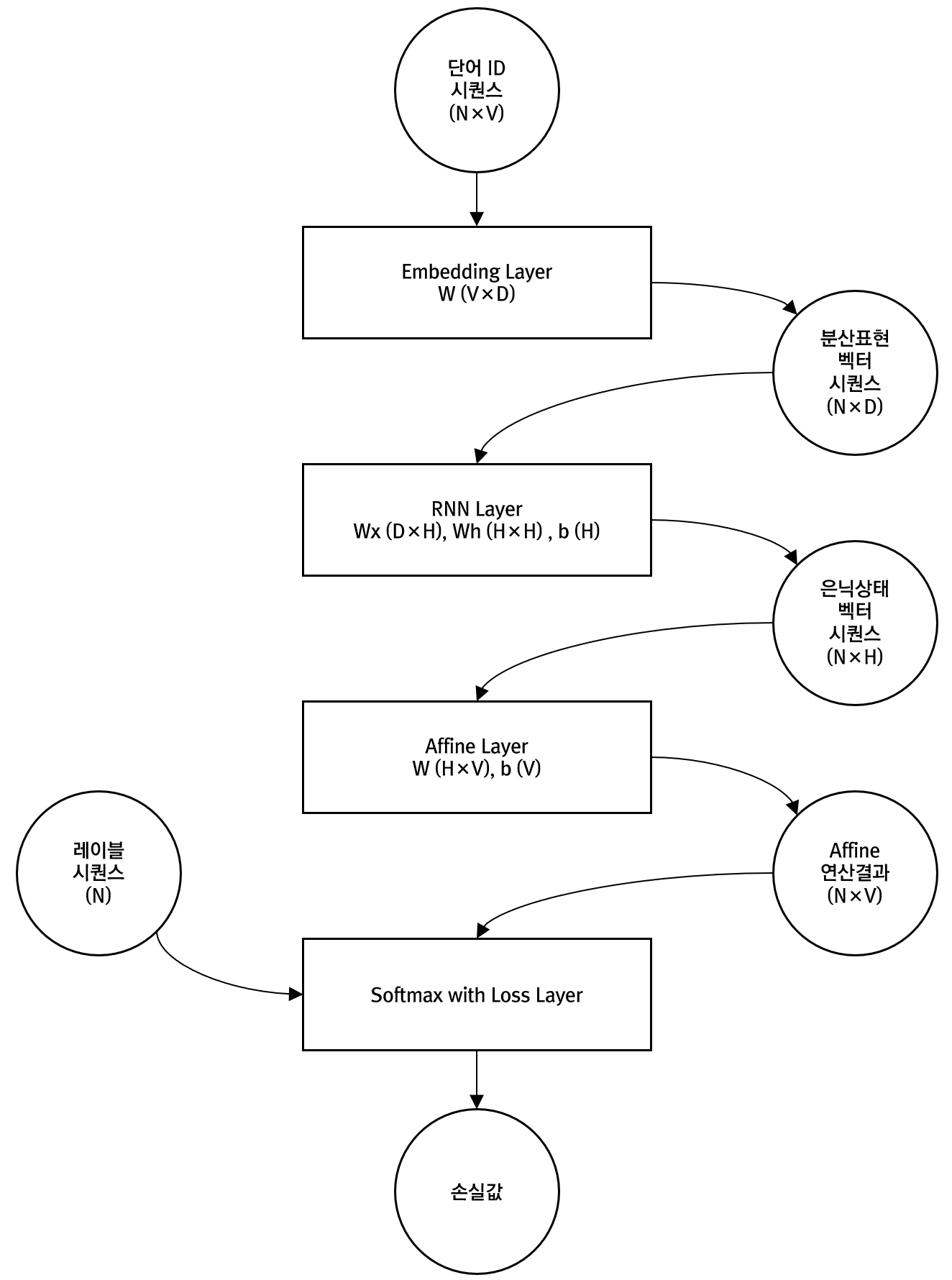
전이 학습(Transfer Learning)은 특정 분야에서 학습된 신경망의 일부 능력을 유사하거나 전혀 새로운 분야에서 사용되는 신경망의 학습에 이용하는 것을 의미합니다.
이미지 분류를 예로 들어 Resnet이나 VGG 등과 같은 신경망의 구성 중 앞단은 CNN 레이어로 구성되어 있습니다. 이 CNN 레이어는 이미지의 특징을 추출하는 능력을 갖는데요. 처음에는 신형성을 추출하고 다음에는 패턴을, 마지막에는 형상 등을 추출한다고 알려져 있습니다. 이러한 이미지의 특징을 추출하는 신경망의 능력은 다른 분야에서도 활용될 수 있습니다. 즉, 수만에서 수천만장의 이미지를 통해 학습된 높은 성능을 갖는 Resnet이나 VGG 신경망의 특징 추출 능력을 그대로 이용하고, 마지막 출력 계층으로써.. 주로 선형(Affine; 가중치와 편향에 대한 행렬 연산) 레이어만을 변경하여 이 변경된 레이어만을 재학습시키는 것이 전이 학습입니다.
전이 학습은 학습 데이터의 수가 적을때도 효과적이며, 학습 속도도 빠릅니다. 그리고 전이학습 없이 학습하는 것보다 훨씬 높은 정확도를 제공한다는 장점이 있습니다.
이 글은 Resnet과 VGG 신경망에 대한 전이학습 코드 중 전이학습을 위한 전처리 코드를 정리합니다. 나머지 학습 등의 코드는 여타 다른 신경망과 동일합니다. 먼저 전이학습을 위한 Resnet 신경망의 전처리 코드입니다.
import torch.nn as nn
from torchvision import models
net = models.resnet18(pretrained=True)
for p in net.parameters():
p.requires_grad = False
fc_input_dim = net.fc.in_features
net.fc = nn.Linear(fc_input_dim, 2)
먼저 이미 학습된 resnet18 신경망을 불러오고, 이 신경망의 가중치가 학습되지 않도록 합니다. 그리고 이 신경망의 마지막 구성 레이어(fully connected layer로써 Affine Layer, Dense layer라고도 함)의 입력 데이터 수를 얻고, 이렇게 얻는 입력 데이터의 수와 출력하고자 하는, 즉 분류 개수인 2에 대한 선형 레이어를 생성하여 신경망을 구성하는 마지막 레이어를 교체합니다. 결과적으로 이 신경망의 마지막 레이어를 제외한 특징 추출 레이어들은 학습되지 않고, 마지막 레이어만이 학습될 것입니다.
참고로 위의 신경망의 구성 레이어를 출력하는 코드와 그 결과는 다음과 같은데, 구성 레이어의 마지막이 fc라는 것을 알 수 있습니다.
for name,module in net.named_children():
print(name)
''' output:
conv1
bn1
relu
maxpool
layer1
layer2
layer3
layer4
avgpool
fc
'''
다음은 VGG 신경망에 대한 전이학습 전처리 코드입니다.
from torchvision import models
net = models.vgg16(pretrained=True)
features = net.features
for params in vgg.features.parameters():
param.requires_grad = False
net.classifier[6].out_features = 2
객체 net을 생성한 후 바로 print(net)을 실행해 보면 다음과 같은 출력을 볼 수 있습니다.
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace=True)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace=True)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace=True)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
(classifier)의 마지막 구성요소[6]을 보면 out_features가 1000으로 되어 있는 것을 볼 수 있고, 이를 분류하고자 하는 개수인 2로 변경하는 전처리 코드였습니다.

![Rendered by QuickLaTeX.com $$loss(x,class)=-\log\biggl(\frac{\exp(x[class])}{\sum_{j}{\exp(x[j])}}\biggr)=-x[class]+\log\biggl(\sum_{j}{\exp(x[j])}}\biggr)$$](http://www.gisdeveloper.co.kr/wp-content/ql-cache/quicklatex.com-f3208d5dfaaecd0f28069ec368ceb1f7_l3.png)