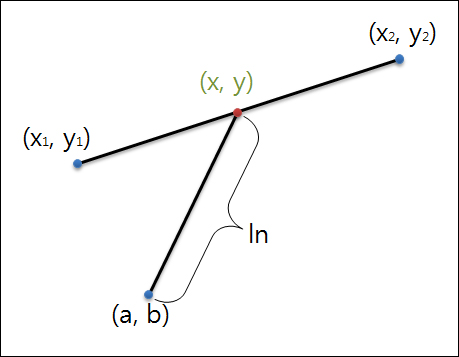
제목이 난해하니 먼저 그림부터 보였습니다. 주어진 선분이 있습니다. 이 선분의 시작점은 (X1, Y1)이고 끝점은 (X2, Y2)입니다. 그리고 주어진 좌표가 있으며 (a, b)입니다. 이 선분과 좌표에 대해서 거리 ln를 가지는 선분상의 좌표를 구하는 것에 대한 정리 포스트입니다. 즉, 위의 그림에서 파란색 점은 주어진 좌표이고 빨간 점을 구하겠다는 것입니다.
먼저 선분에 대한 아래와 같은 매개변수 방정식을 정합니다.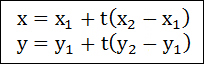
우리가 구해야할 점은 선분상의 점이니 위의 매개변수 방정식에서 x와 y가 바로 우리가 원하는 값입니다. 이 x와 y를 구하기 위해서는 매개변수 t를 구하면 됩니다. 아시겠지만 t가 주어진 선분위에 존재하려면 0~1사이의 값이여야 합니다. 이 값을 벗어나면 답은 없음… 입니다.
이 한가지 관계만 가지고는 않됩니다. 또 하나의 관계를 맺어줘야 합니다. 그 관계는 주어진 좌표(a, b)와 구하고자 하는 선분상의 점(x, y)사이의 거리가 값 ln이라는 사실로부터 다음과 같은 식을 얻을 수 있습니다.![]()
이제 처음 선분에 대한 방정식을 위의 방정식의 x, y에 대입하고 t에 대해 정리를 하면 아래와 같은 t에 대한 2차 방정식이 도출되며 이 2차 방정식을 근의 공식을 통해 t를 구해 보면 다음과 같습니다.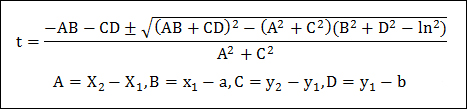
이렇게 구한 t에 대해서 범위가 0~1사이 인지를 검사하고 이 범위에 있다면 이 t를 선분의 방정식에 대입하여 구한 (x, y)가 구하고자 하는 좌표입니다.
타원의 방정식
이 얼마나 오랜만에 써보는 포스팅인지 모르겠습니다. 요즘 이러 저런 일로 바쁘다보니 블로그 관리에 매우 소홀했습니다. 이제 부터라도 짬짬히 시간을 내어.. 일상 업무에서 찾은 내용을 올리도록 노력 해야겠습니다. 해서… 알고보면 매우 간단한 내용이지만 포스팅 하나 올려봅니다.
오늘, 열심히 코드를 작성하던 중에.. 2차원에서 타원을 구성하는 좌표를 뽑아 낼 필요가 있었습니다. Needs는 하나의 타원과 또 다른 하나의 폴리곤을 하나의 도형으로 합(Union)하는 연산이 필요할듯 한데… 타원에 대한 정보는 단순히 중심점과 장반경 그리고 단반경만을 가지고 있음으로 폴리곤에 바로 합할 수 없는지라.. 일단 타원을 구성하는 정점을 이용하여 폴리곤으로 만들고.. 폴리곤과 폴리곤의 합 연산을 통해 원하는 결과를 얻고자 함이였습니다.
간단히 타원의 공식은 인터넷(http://en.wikipedia.org/wiki/Ellipse)을 통해 아래처럼 얻었습니다. 물론 프로그래밍에서 쉽게 사용할 수 있는 매개변수방정식으로 말입니다.
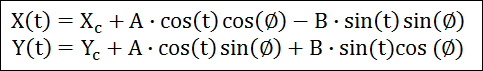
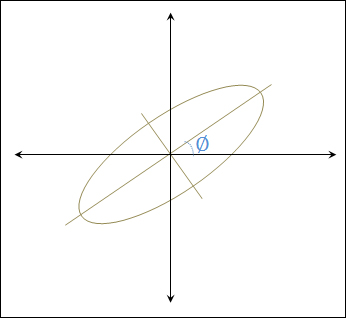
위의 식에서 Xc와 Yc는 타원의 중심입니다. 그리고 A와 B는 각각 X축과 Y축에 대한 타원의 반경이며 각각을 장축과 단축이라고 하겠습니다. 그리고 t는 0도에서 360도까지의 범위입니다. 물론 0도와 360도는 동일하므로 둘 중 하나는 포함되지 않아야 합니다. 마지막으로 ∅는 장축과 X축이 이루는 각도 입니다. 즉 ∅를 통해 기울어진 타원을 구성하는 좌표를 정의할 수가 있습니다. ∅에 대한 이해를 돕기 위해 아래 그림을 참고 하시기 바랍니다.