주식 종목에 대한 하루 단위의 시가, 종가, 거래량 등을 웹을 통해 얻을 수 있는데요. 이러한 데이터를 파이썬을 이용해, 네이버의 주식 서비스로부터 얻는 코드에 대해 설명합니다.
코드는 다음과 같습니다. 원하는 종목에 대해 원하는 페이지만큼.. (이 부분은 주식 서비스마다 가능 여부 및 방식이 달라짐) 정보를 얻어옵니다.
import requests
from bs4 import BeautifulSoup
def print_stock_price(code, page_num):
result = [[], [], [], [], [], [], [], [], []]
for n in range(page_num):
url = 'https://finance.naver.com/item/sise_day.nhn?code='+code+'&page='+str(n+1)
print(url)
r = requests.get(url)
if not r.ok:
print('Not more data !')
break
html = r.content
soup = BeautifulSoup(html, 'html.parser')
tr = soup.select('table > tr')
for i in range(1, len(tr)-1):
td = tr[i].select('td')
if td[0].text.strip():
result[0].append(td[0].text.strip()) # 날짜
result[1].append(td[1].text.strip()) # 종가
img = td[2].select('img')
if len(img) != 0:
if 'src' in img[0].attrs:
src = img[0]['src']
if 'up' in src: result[2].append('상승')
else: result[2].append('하락')
else: result[2].append('보합')
result[3].append(td[2].text.strip()) # 전일대비
result[4].append(td[3].text.strip()) # 시장가
result[5].append(td[4].text.strip()) # 최고가
result[6].append(td[5].text.strip()) # 최저가
result[7].append(td[6].text.strip()) # 거래량
for i in range(len(result[0])):
# 날짜 종가 상승/하락/보합+a 시장가 최고가 최저가 거래량
print(result[0][i], result[1][i], result[2][i]+result[3][i], result[4][i], result[5][i], result[6][i], result[7][i])
print_stock_price(code='005930', page_num=1)
코드를 보면, print_stock_price 함수의 url 변수에 저장된 주소에 대한 결과 DOM을 해석하고 있는 것을 알 수 있습니다. 즉, DOM에 대한 구조를 먼저 파악해야 한다는 것이 핵심인데요. 위의 코드가 정상적으로 작동할 당시의 실제 DOM의 한가지 예는 다음과 같습니다.
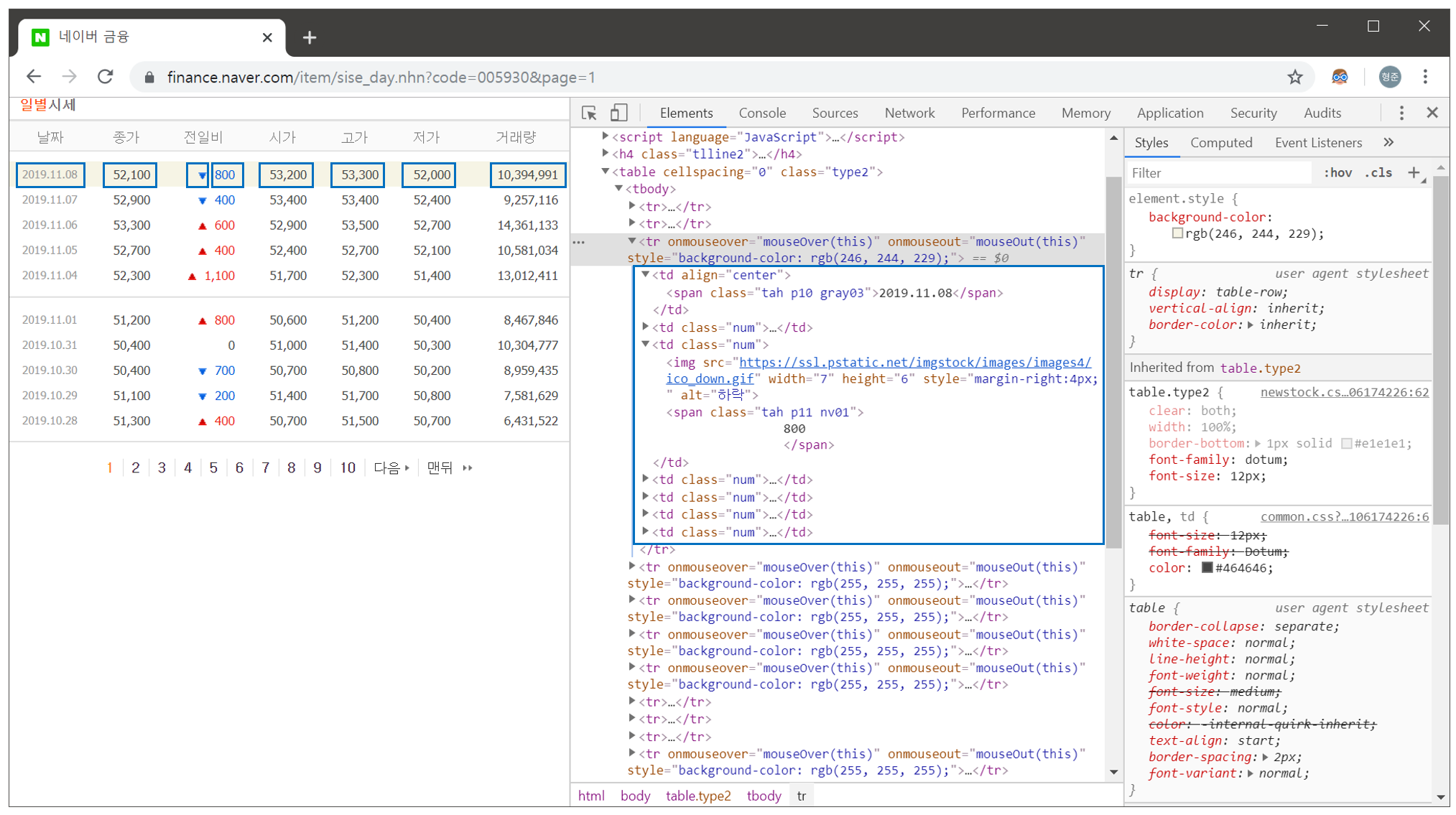
코드와 추출하고자 하는 DOM 요소가 명확하게 1:1로 매칭되고 있는 것을 확인할 수 있습니다.