GPU가 여러개 설치된 컴퓨터에서 TensorFlow를 사용할 경우 일반적으로 가장 첫번째(0)의 GPU를 사용하게 되는데.. 이때 아래의 코드를 통해 두번째(1)의 GPU를 사용하라고 지정할 수 있음
import tensorflow as tf import os os.environ["CUDA_VISIBLE_DEVICES"] = "1"

공간정보시스템 / 3차원 시각화 / 딥러닝 기반 기술 연구소 @지오서비스(GEOSERVICE)
GPU가 여러개 설치된 컴퓨터에서 TensorFlow를 사용할 경우 일반적으로 가장 첫번째(0)의 GPU를 사용하게 되는데.. 이때 아래의 코드를 통해 두번째(1)의 GPU를 사용하라고 지정할 수 있음
import tensorflow as tf import os os.environ["CUDA_VISIBLE_DEVICES"] = "1"
딥러닝 신경망을 이용하여 항공영상의 해상도를 강화하는 GeoAI의 기술중 하나를 소개합니다. 흔히 슈퍼 레졸루션(Super Resolution)이라 불리며, 25cm 급 해상도의 항공영상을 통해 학습 DB를 구축하여 Super Resoultion에 대한 신경망을 학습한 후 그 결과를 정리하였습니다.
저해상도 영상을 고해상도 영상으로 만들기 위한, 신경망을 활용하기 이전의 방법은 인접 픽셀간의 보간을 통한 Bicubic Interpolation 방식, 이미지 데이터베이스에서 유사한 장면의 이미지를 선택해 그 이미지를 결과로 하는 Best Scene Match 방식, 좀더 큰 유사한 패턴을 가져와 작은 패턴 위치에 붙여 넣는 Self-Similarity 기반 방식 등이 있었고, 그 후 신경망을 활용하여 더욱 성능이 향상된, 또한 보다 범용적으로 활용할 수 있게 되었습니다.

위의 그림(출처: EXTREMETECH)은 Orignal 영상을 2배 확대했을 때, 가장 가까운 픽셀을 활용한 보간법을 통한 방법인 Nearest Neighbor 방식과 Super Resolution 방식의 결과 비교입니다. 바로 이러한 Super Resolution을 저해상도의 항공영상에 적용하여 더 높은 해상도를 가지는 영상을 생성하는데 활용할 수 있습니다.
딥러닝 신경망을 활용한 해상도 강화는 Convolutional Layer를 사용하는 CNN을 이용한 모델로 시작하여, Skip-Connection 기법(잔차 연결;Residual-Connection 또는 숏컷;Short-Cut이라고도 함)을 적용한 VDSR 모델로 발전하였고, 다음에는 적대적 생성 신경망인 GAN을 활용한 SRGAN 모델이 연구 되었습니다. VDSR 모델은 기본적으로 CNN의 사용에 Skip-Connection 기법을 추가한 것이고, SRGAN 모델은 CNN 및 VDSR에서 의미 있게 사용한 Skip-Connection 기법을 Generator에 적용한 GAN 방식으로, 이전의 기반 기술을 새로운 기술에서 보다 효과적으로 활용하고 있음을 알 수 있습니다.
Super Resolution은 저해상도의 이미지를 고해상도의 이미지로 만들어 주는 기술입니다. 이를 위한 신경망 학습에는 저해상도의 이미지와 해당 저해상도 이미지에 대한 고해상도 이미지가 필요 합니다. 이를 위해 먼저 많은 고해상도 이미지를 작은 크기로 줄여 저해상도 이미지로 만들 수 있고, 이렇게 만든 저해상도 이미지를 입력 데이터로, 원래의 고해상도 데이터를 정답인 레이블 데이터로 사용하게 됩니다. 즉, 레이블 데이터는 사람이 별도로 구축하지 않고, 학습시 자동으로 생성해 낼 수 있어 더욱 활용도가 매우 높은 기술입니다.
이 글은 적대적 생성 신경망인 GAN을 이용하여 항공영상의 해상도를 향상시키는 신경망에 대한 구현 사례에 대한 결과를 소개하는데 초점을 맞췄으며, GAN에 대한 보다 상세한 기술적 내용과 구현은 다음 글을 참고하기 바랍니다.
GAN은 기본적으로 생성자(Generator)와 판별자(Discriminator)에 대한 모델 2개가 필요하며, 본 사례에서 사용한 사용한 신경망 모델은 다음과 같습니다.
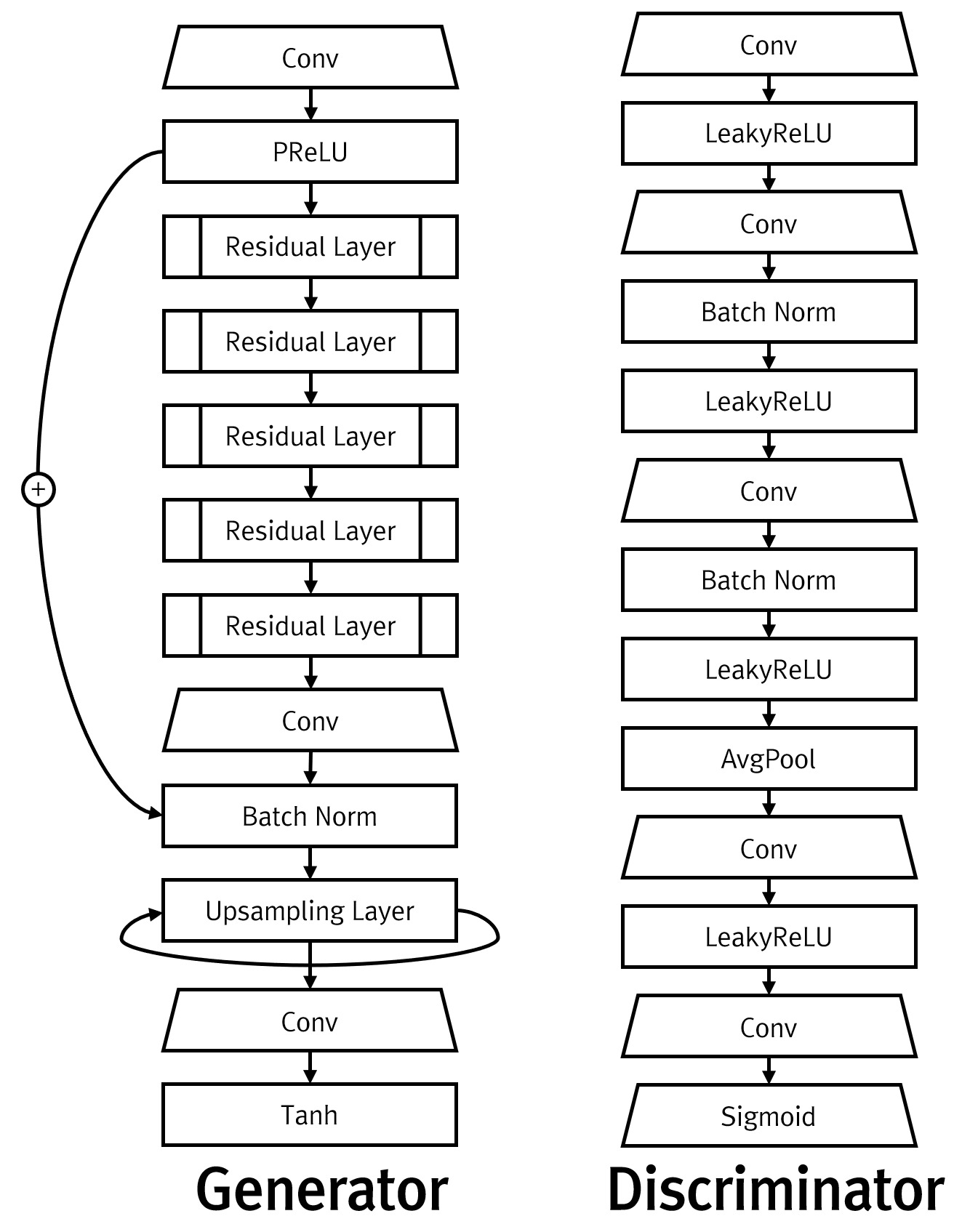
위의 Generator와 Discriminator 신경망 모델의 학습에는 25cm급 항공영상을 1/8 크기로 줄여 해상도를 대폭 낮췄습니다. 즉, 25cm 급을 200cm 급으로 낮춘 것으로 샘플 중 3가지만 언급하면 다음과 같습니다.

원본 이미지에 비해 그 품질이 현격히 낮아진 것을 확인할 수 있습니다. 이처럼 낮아진 저해상도 영상을 상대적으로 더 향상시키고자 먼저 보유하고 있는 항공영상을 768×768 픽셀 크기로 잘라내어, 총 3766개의 학습 영상을 구축했습니다. 이 학습 데이터를 활용하여 총 50 번의 신경망 학습을 수행했을 때, 결과는 다음과 같았습니다. 아래의 결과는 신경망이 학습시에 한번도 보지 못한 영상에 대한 결과입니다. 각 줄의 첫번째가 입력값인 저해상도 영상이고 세번째가 저해상도 영상을 Super Resolution으로 향상시킨 결과입니다. 가운데 이미지는 저해상도 이미지를 생성해 내기 위한 원본 이미지로써 신경망 학습 시 정답으로 사용되는 레이블 데이터입니다.







위의 결과는 GAN 방식을 이용한 Super Resolution입니다. 이외에 기본적인 CNN만을 사용한 모델과 학습을 좀더 잘되게 하기 위해 Skip-Connection 기법을 적용한 VDSR 등이 있다고 앞서 언급했습니다. 이 셋 모두 저해상도 이미지를 고해상도 이미지로 변환하기 위해 이미지의 크기를 확대하기 위한 방법으로 Transposed Convolutional 방식과 Sub-Pixel 방식이 있어, 대상이 되는 이미지의 성격에 따라 어떤 모델을, 세부적으로는 모델을 구성하는 레이어를 어떻게 구성할지를 결정해야 합니다. 또한 최적의 하이퍼파라메터도 반복적인 학습 및 검증을 통해 다양하게 조정해야 합니다.
또한 구슬이 서말이라도 꿰어야 보배라고 하듯이 Super Resolution을 이용한 항공영상이나 위성영상의 해상도를 보강하는 기술이 실제 상황에 사용하기 위해서는 단순이 딥러닝의 신경망 학습과 의미있는 결과 도출만으로는 충분하지 않습니다. 이러한 신경망의 의미있는 결과를 실제 대용량의 영상에 적용하고 실제 사용자가 사용할 수 있는 효과적 UI과 성능을 갖춘 어플리케이션으로 개발되어야 할 것입니다.
저해상도의 위성영상이나 항공영상을 고해상도로 개선시키기 위한 Super Resolution에 대한 신경망 학습 데이터입니다. 훈련 데이터와 테스트 데이터로 구분했으며, 각각 3766개와 191개로 구성되어 있습니다. 각 이미지의 크기는 768×768이며 RGB 3 채널로 구성되어 있습니다.
데이터셋의 내용과 실제 위의 데이터셋을 이용해 학습된 신경망을 통한 결과는 다음과 같습니다. 각 줄의 첫번째 열는 두번째 열의 이미지로부터 1/8 크기로 줄여 생성한 저해상도이고, 두번째 열 이미지가 실제 데이터셋입니다. 세번째 열의 이미지는 저해상도 이미지가 Super Resolution을 통해 해상도가 향상된 결과 영상입니다.



딥러닝 신경망을 활용한 Super Resolution에 대한 보다 자세한 내용은 다음 글을 참고하시기 바랍니다.
GAN은 Generative Adversarial Network로 적대적 생성 신경망입니다. 즉, 무언가를 생성하는 신경망인데.. 그 무언가를 제대로 잘생성하기 위해 누군가를 잘속이기 위한 전략을 취합니다. 흔히 GAN에 대한 이러한 설명을 위조지폐범과 지폐판별사의 예를 많이 듭니다. 위조지폐범은 위조지폐를 만들어 지폐판별사에게 전달하면 판별사는 이게 가짜인지 진짜인지를 판별해서 지폐범에게 얼마나 가짜같은지를 알려주고, 위조지폐범은 판별사에게서 얻은 피드백을 통해 좀더 진짜같은 위조지폐를 만들어 다시 판별사에게 전달합니다. 이러한 과정을 반복하다보면 위조지폐범은 더욱 진짜 같은 위조지폐를 만들 수 있게 된다는 것입니다. 이러한 설명을 도식으로 표현해 보면 다음과 같습니다.
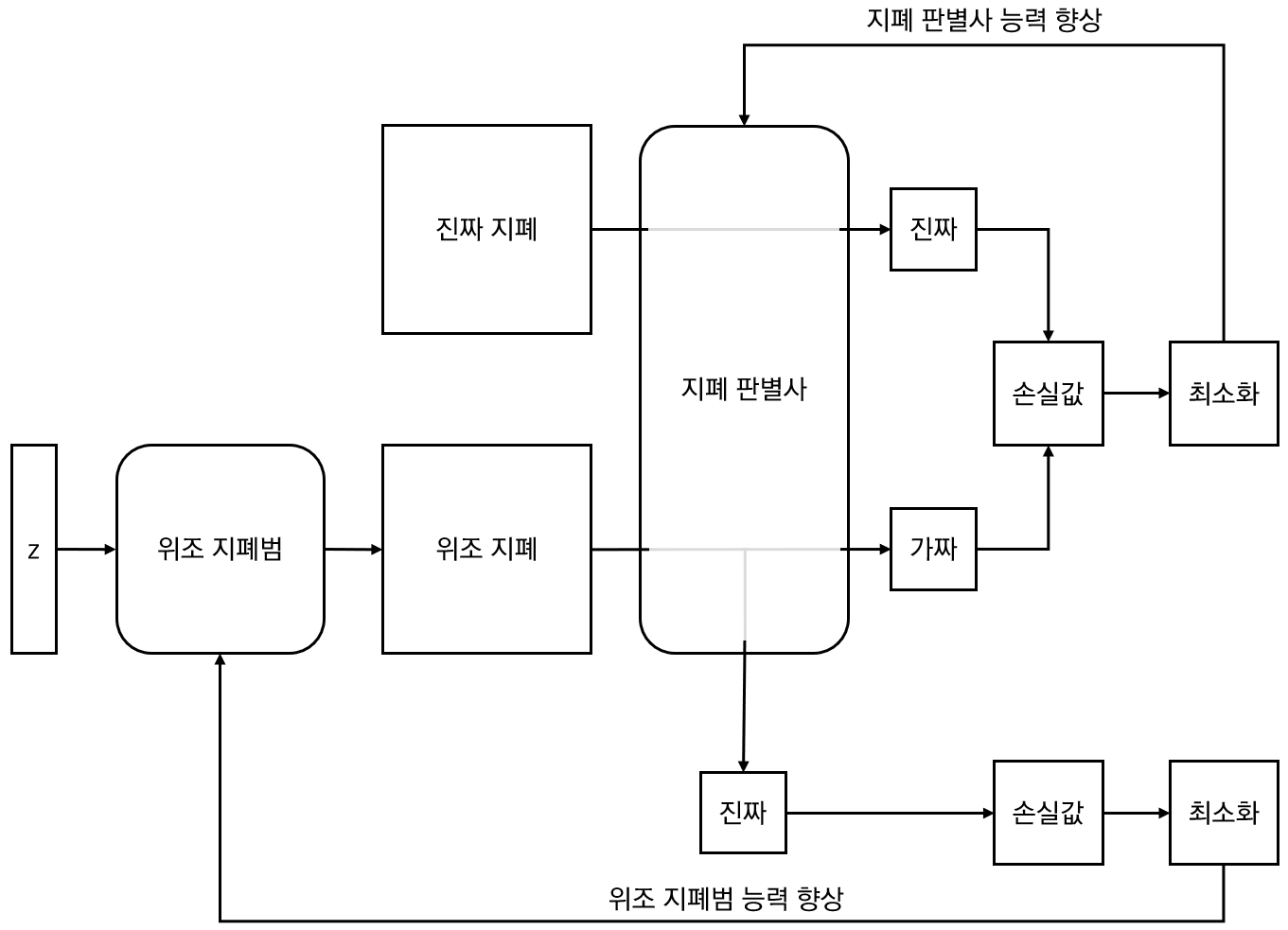
위의 그림에서 위조 지폐범과 지폐 판별사는 각각 신경망 모델입니다. 이 두 신경망 모델 학습을 위해 학습시 얻어지는 손실값 최소화를 통해 신경망의 능력을 향상시켜나가게 됩니다. GAN은 위조지폐처럼 이미지를 생성하는 것뿐만 아니라 입력 데이터에 따라 텍스트나 작곡 등도 가능합니다. 또한 GAN은 레이블 데이터가 필요없는 비지도학습에 속합니다. 즉, GAN을 통해 생성하고자 하는 종류의 데이터만 있으면 됩니다. 초기의 GAN은 단순한 Linear Layer(선형 레이어)만으로 구성할 수 있습니다. 그러나 생성하고자 하는 데이터에 따라… 즉 이미지의 경우는 Convolutional Layer로 구성하는 것이 효과적입니다. 이 글에서는 이 두가지 경우 모두를 언급합니다.
먼저 선형 레이어만으로 구성된 GAN에 대한 실제 구현입니다.
딥러닝을 위한 라이브러리로 PyTorch를 사용하므로 다음처럼 필요한 라이브러리 등을 불러옵니다.
import os import torch import torch.nn as nn import torchvision import torch.optim as optim from torchvision import transforms, datasets import matplotlib.pyplot as plt import numpy as np
다음으로 반복 학습수와 배치수, 그리고 GPU를 지원하는지의 여부에 따른 준비를 다음 코드를 통해 지정합니다.
EPOCHS = 1000
BATCH_SIZE = 128
USE_CUDA = torch.cuda.is_available()
DEVICE = torch.device("cuda" if USE_CUDA else "cpu")
우리가 생성할 이미지 데이터는 MNIST의 숫자 데이터입니다. 보다 복잡한 이미지도 가능하지만, 여기서는 빠른 학습과 분명한 결과 확인을 위해 MNSIT 숫자 데이터를 사용했습니다.
trainset = datasets.MNIST("./data", train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
)
train_loader = torch.utils.data.DataLoader(dataset = trainset, batch_size=BATCH_SIZE, shuffle=True, drop_last=True)
앞서 그림을 보면 위조지폐범에 z 값이 입력되고 있는 것을 볼 수 있습니다. 이 z는 잠재 벡터(Latent Vector)인데요. 이 잠재 벡터의 구성 값에 따라 어떤 이미지가 생성되는지 결정됩니다. 이 잠재 벡터를 구성하는 값의 개수를 아래 코드로 정의합니다.
z_size = 72
이제 이미지를 생성하는 신경망 모델을 정의합니다.
class GNet(nn.Module):
def __init__(self):
super().__init__()
self._layers = nn.Sequential(
nn.Linear(z_size, 128),
nn.ReLU(),
nn.Linear(128, 256),
nn.ReLU(),
nn.Linear(256, 512),
nn.ReLU(),
nn.Linear(512, 784),
nn.Tanh()
)
def forward(self, x):
return self._layers(x)
잠재 벡터의 크기값만큼 입력받아 최종적으로 이미지의 크기인 784(이미지 크기: 28×28)로 출력합니다. 원활한 학습을 위해 활성화함수로 ReLU를 사용했고, 마지막 활성화함수는 Tanh를 사용했는데.. 이는 이미지를 구성하는 값들의 범위가 -1~1이고, 이를 맞춰주기 위해 Tanh를 사용한 것입니다.
다음은 이미지의 진짜와 가짜를 판별하는 신경망 모델입니다.
class DNet(nn.Module):
def __init__(self):
super().__init__()
self._layers = nn.Sequential(
nn.Linear(784, 512),
nn.LeakyReLU(0.25),
nn.Linear(512, 256),
nn.LeakyReLU(0.25),
nn.Linear(256, 128),
nn.LeakyReLU(0.25),
nn.Linear(128,1),
nn.Sigmoid()
)
def forward(self, x):
return self._layers(x)
이제 두개의 신경망을 학습하기 위해 두 신경망을 생성하고, 손실값 계산을 위해 Binary Cross Entropy Loss인 BCELoss를 사용합니다. 또한 손실값에 대한 경사하강을 통해 가중치들의 최적화를 위한 Adam을 사용합니다. 생성자와 판별자 각각을 학습해야 하므로 최적화를 위한 객체는 각각을 위해 2개가 필요합니다. 그리고 이미지가 진짜인지, 가짜인지에 대한 레이블 데이터를 생성해 둡니다.
D = DNet().to(DEVICE) G = GNet().to(DEVICE) criterion = nn.BCELoss() d_optimizer = optim.Adam(D.parameters(), lr=0.0002) g_optimizer = optim.Adam(G.parameters(), lr=0.0002) real_labels = torch.ones(BATCH_SIZE, 1).to(DEVICE) fake_labels = torch.zeros(BATCH_SIZE, 1).to(DEVICE)
이제 실제 신경망의 학습 코드입니다.
fig, axes = plt.subplots(4,3)
for epoch in range(EPOCHS):
for i, (images, _) in enumerate(train_loader):
images = images.reshape(BATCH_SIZE, -1).to(DEVICE)
outputs = D(images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
z = torch.randn(BATCH_SIZE, z_size).to(DEVICE)
fake_images = G(z)
outputs = D(fake_images.detach())
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs
d_loss = d_loss_real + d_loss_fake
d_optimizer.zero_grad()
d_loss.backward()
d_optimizer.step()
outputs = D(fake_images)
g_loss = criterion(outputs, real_labels)
g_optimizer.zero_grad()
g_loss.backward()
g_optimizer.step()
print('Epoch[{:3d}/{:3d}] d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'.format(
epoch, EPOCHS, d_loss.item(), g_loss.item(), real_score.mean().item(), fake_score.mean().item()))
z = torch.randn(BATCH_SIZE, z_size).to(DEVICE)
fake_images = G(z)
for row in range(4):
for col in range(3):
fake_images_img = np.reshape(fake_images.data.cpu().numpy()[row*4+col],(28,28))
axis = axes[row][col]
axis.get_xaxis().set_ticks([])
axis.get_yaxis().set_ticks([])
axis.imshow(fake_images_img, cmap='gray')
plt.savefig('./data/DNN_GAN_{:03d}.jpg'.format(epoch))
매 학습 단계마다 학습된 신경망으로 12개의 이미지를 생성해 저장하도록 하였습니다. 각 학습 단계에서는 먼저 진짜 이미지와 가짜 이미지를 판별자에게 판별하도록 하고 판별시 얻어지는 손실값을 합하여 역전파하여 최소화으로써 판별자를 학습시킵니다. 그리고 판별자를 통해 가짜 이미지를 진짜 이미지라고 판별하라고 했을때 발생하는 손실값을 역전파하여 최소화함으로써 생성자를 학습시킵니다.
GAN은 많은 학습이 필요하므로 상당한 시간이 소요됩니다. 아래는 각 에폭 단위별 순서대로 생성된 결과입니다.

선형 레이어만으로 GAN을 구현하면 학습이 더디게 걸린다는 문제와 높은 품질의 결과와 좀더 다양한 이미지들이 생성되지 않는다는 문제가 있습니다. 이를 해결하기 위해서는 이미지 생성을 위한 GAN에 Convolutional Layer를 적용한 DCGAN(Deep Convolutional GAN)에 대해 설펴 보겠습니다.
DCGAN과 GAN의 차이점은 신경망의 구성뿐입니다. 물론 신경망이 변경되므로 입력되는 데이터, 즉 텐서들의 차원이 변경되는 부분 역시 신경을 써줘야 합니다. DCGAN의 신경망 코드와 신경망에 입력되는 텐서들의 차원 변경에 따른 코드는 신경망 학습 코드에서 나타나므로 신경망 학습 부분에 대한 코드만을 살펴 보겠습니다. 먼저 DCGAN의 생성자와 판별자에 대한 신경망 코드입니다.
class GNet(nn.Module):
def __init__(self):
super().__init__()
self._layers = nn.Sequential(
nn.ConvTranspose2d(z_size, 32, 3, 1, 0, bias=False), # 1 -> 3
nn.BatchNorm2d(32),
nn.ReLU(inplace=False),
nn.ConvTranspose2d(32, 16, 4, 2, 1, bias=False), # 3 -> 6
nn.BatchNorm2d(16),
nn.ReLU(inplace=False),
nn.ConvTranspose2d(16, 8, 4, 2, 0, bias=False), # 6 -> 14
nn.BatchNorm2d(8),
nn.ReLU(inplace=False),
nn.ConvTranspose2d(8, 1, 4, 2, 1, bias=False), # 14 -> 28
nn.Tanh()
)
def forward(self, x):
return self._layers(x)
class DNet(nn.Module):
def __init__(self):
super().__init__()
self._layers = nn.Sequential(
nn.Conv2d(1, 8, 4, 2, 1, bias=False), # 28 -> 14
nn.BatchNorm2d(8),
nn.LeakyReLU(0.2, inplace=False),
nn.Conv2d(8, 16, 4, 2, 1, bias=False), # 14 -> 7
nn.BatchNorm2d(16),
nn.LeakyReLU(0.2, inplace=False),
nn.Conv2d(16, 32, 4, 2, 1, bias=False), # 7 -> 3
nn.BatchNorm2d(32),
nn.LeakyReLU(0.2, inplace=False),
nn.Conv2d(32, 1, 4, 2, 1, bias=False), # 3 -> 1
nn.Sigmoid(),
)
def forward(self, x):
return self._layers(x).squeeze()
Convolution Layer로써 생성자에서는 ConvTranspose2d를 사용하여 잠재 벡터(z)로 시작해 이미지를 점차 키워나가며 생성하고, 판별자에서는 Conv2d를 사용하여 이미지의 특성을 추출하다가 마지막에 Sigmoid 함수를 통해 0~1사이의 값을 뽑아냅니다. 이 값이 바로 이미지가 가짜(0)인지 진짜(1)인지에 대한 판별 여부입니다. Convolutional Layer는 이미지를 대상으로 하므로 입력 이미지의 크기와 마지막 출력 이미지의 크기를 원하는 크기에 맞추기 위해 Filter와 Stride, Padding 등의 값을 조정해줘야 합니다. 아래는 이럴때 사용할 수 있는 수식입니다.
먼저 nn.ConvTranspose2d 연산을 통해 입력 이미지의 크기가 어떤 크기의 출력 이미지로 변경되는지에 대한 수식입니다.
![]()
다음은 nn.Conv2d 연산을 통해 입력 이미지의 크기가 어떤 크기의 출력 이미지로 변경되는지에 대한 수식입니다. 결과의 소수점은 버립니다.
![]()
그리고 다음은 학습 코드입니다. 앞서 언급한 것처럼 코드 구성은 GAN과 동일하고 입력 데이터의 차원 크기에 의한 미세한 변화가 있을뿐입니다.
fig, axes = plt.subplots(4,3)
for epoch in range(EPOCHS):
for i, (images, _) in enumerate(train_loader):
images = images.to(DEVICE)
outputs = D(images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
z = torch.randn(BATCH_SIZE, z_size, 1, 1).to(DEVICE)
fake_images = G(z)
outputs = D(fake_images.detach())
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs
d_loss = d_loss_real + d_loss_fake
d_optimizer.zero_grad()
d_loss.backward()
d_optimizer.step()
outputs = D(fake_images)
g_loss = criterion(outputs, real_labels)
g_optimizer.zero_grad()
g_loss.backward()
g_optimizer.step()
print('Epoch[{:3d}/{:3d}] d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'.format(
epoch, EPOCHS, d_loss.item(), g_loss.item(), real_score.mean().item(), fake_score.mean().item()))
z = torch.randn(BATCH_SIZE, z_size, 1, 1).to(DEVICE)
fake_images = G(z)
for row in range(4):
for col in range(3):
fake_images_img = np.reshape(fake_images.data.cpu().numpy()[row*4+col],(28,28))
axis = axes[row][col]
axis.get_xaxis().set_ticks([])
axis.get_yaxis().set_ticks([])
axis.imshow(fake_images_img, cmap='gray')
plt.savefig('./data/CNN_GAN_{:03d}.jpg'.format(epoch))
실행해보면 GAN보다 DCGAN이 더 빨리 의미있는 이미지를 생성해 내기 시작합니다. 또한 보다 더 높은 품질의, 더 다양한 이미지를 생성해 보내는 것을 확인할 수 있습니다. 아래는 DCGAN에 의한 각 에폭 단위별 순서대로 생성된 결과입니다.

건물과 비닐하우스에 대한 검출(Detection)용 학습 DB입니다. 구축된 건물수는 약 6000개 이상, 비닐하우스는 약 2000개 이상입니다. DB 포맷은 COCO Dataset 입니다. 필요하신 분들은 자유롭게 사용하시기 바라며 사용에 대해 어떠한 제약도 없습니다. 학습 데이터수와 검증 데이터 수의 비율은 통상 9:1 또는 8:2지만 본 DB는 이 비율이 아니므로 필요할 경우 비율을 맞추시기 바랍니다.
아래의 이미지는 본 학습 DB를 이용해 학습된 신경망에 대한 검출 결과입니다.
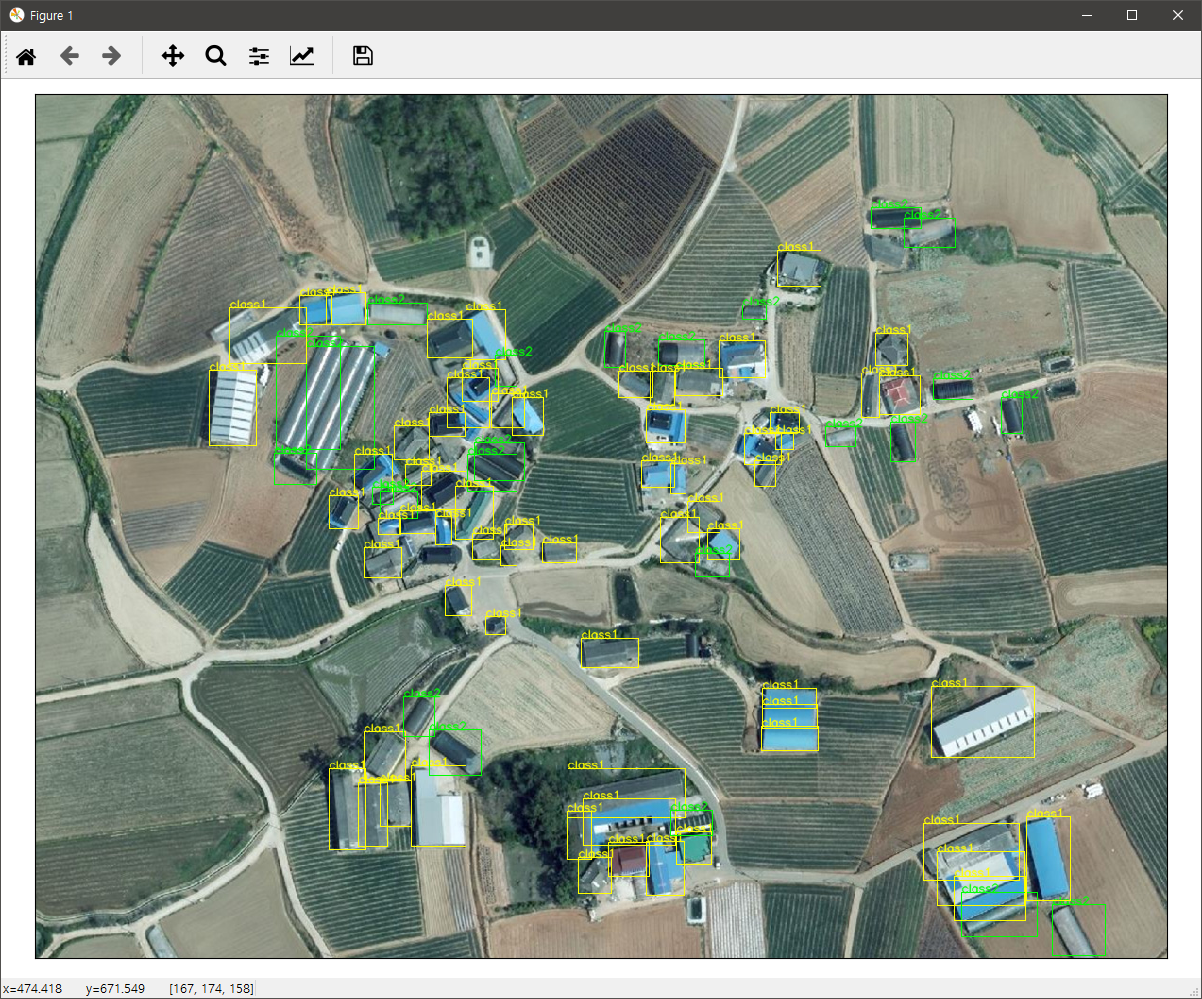
본 학습 DB를 이용해 학습된 신경망의 결과에 대한 보다 자세한 내용은 아래의 글을 참고하시기 바랍니다.