아래와 같은 식을 회귀하는 모델을 구하는 두가지 접근을 PyTorch로 살펴본다.
![]()
즉, 입력값(a, b)에 대한 출력값 y가 100개 주어지고, 이 데이터를 통해 상수항인 1과 계수 5, 7을 구하는 것이 문제다. 물론 y에는 오차가 반영되어 있다. 첫번째 접근은 다음과 같다. 손실함수는 평균최소제곱을, 역전파를 통한 최적값 수렴을 위한 기울기를 구해 반영한 학습률은 0.01을 사용했다. 아래의 코드의 경우 기울기를 구하기 위한 방법을 PyTorch의 역전파를 이용한 것이다.
import torch
from matplotlib import pyplot as plt
weight_true = torch.Tensor([1,5,7]) # y = 1 + 5a + 7b
X = torch.cat([torch.ones(100,1),torch.randn(100,2)], 1)
y = torch.mv(X, weight_true) + torch.randn(100)
weight = torch.randn(3, requires_grad=True)
lr = 0.01
losses = []
for epoch in range(1000):
weight.grad = None
y_pred = torch.mv(X, weight)
loss = torch.mean((y - y_pred)**2)
loss.backward()
weight.data = weight.data - lr*weight.grad.data
losses.append(loss.item())
print(weight)
plt.plot(losses)
plt.show()
두번째 접근은 다음과 같다. 앞서 직접 하나 하나 개발자가 지정했던 것들에 대한 모듈을 사용한 경우이다.
import torch
from torch import nn, optim
from matplotlib import pyplot as plt
weight_true = torch.Tensor([1,5,7]) # y = 1 + 5a + 7b
X = torch.cat([torch.ones(100,1),torch.randn(100,2)], 1)
y = torch.mv(X, weight_true) + torch.randn(100)
net = nn.Linear(in_features=3, out_features=1, bias=False)
optimizer = optim.SGD(net.parameters(), lr=0.01)
loss_fn = nn.MSELoss()
losses = []
for epoch in range(1000):
optimizer.zero_grad()
y_pred = net(X)
loss = loss_fn(y_pred.view_as(y), y)
loss.backward()
optimizer.step()
losses.append(loss.item())
print(net.weight)
plt.plot(losses)
plt.show()
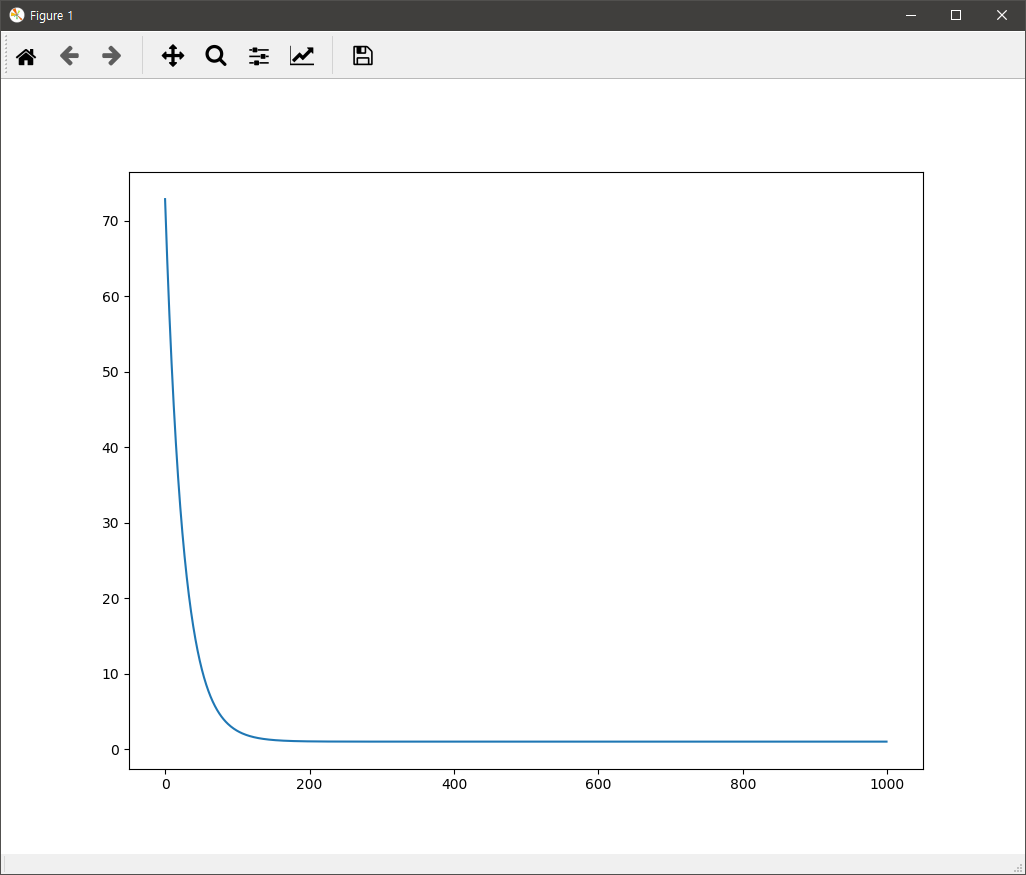
두 경우 모두 실행하면 아래와 같은 손실값에 대한 그래프와 추론된 상수와 두계수 값이 콘솔에 출력된다.
함수들에 대한 그래프 시각화
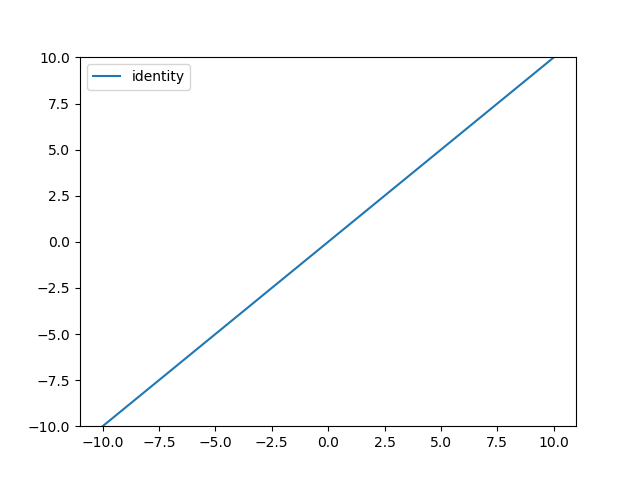
선형 함수에 대한 정의와 그래프 시각화는 다음 코드와 같다.
import numpy as np
import matplotlib.pylab as plt
def identity_func(x):
return x
x = np.arange(-10, 10, 0.01)
plt.plot(x, identity_func(x), linestyle='-', label="identity")
plt.ylim(-10, 10)
plt.legend()
plt.show()
결과는 다음과 같다.
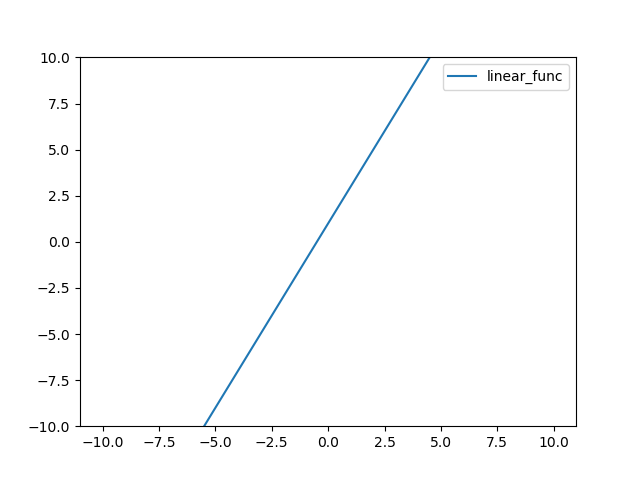
기울기와 y절편을 고려한 선형 함수의 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def linear_func(x):
return 2 * x + 1
x = np.arange(-10, 10, 0.01)
plt.plot(x, linear_func(x), linestyle='-', label="linear_func")
plt.ylim(-10, 10)
plt.legend()
plt.show()
결과는 다음과 같다.
계단함수에 대한 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def binarystep_func(x):
return (x>=0)*1
x = np.arange(-10, 10, 0.01)
plt.plot(x, binarystep_func(x), linestyle='-', label="binarystep_func")
plt.ylim(-5, 5)
plt.legend()
plt.show()
결과는 다음과 같다.
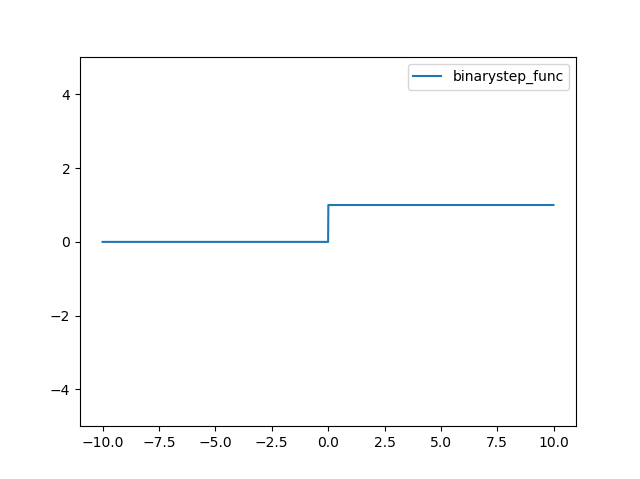
로지스틱(Logistic) 또는 시그모이드(Sigmoid)라고 불리는 함수 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softstep_func(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-10, 10, 0.01)
plt.plot(x, softstep_func(x), linestyle='-', label="softstep_func")
plt.ylim(0, 1)
plt.legend()
plt.show()
결과는 다음과 같다.
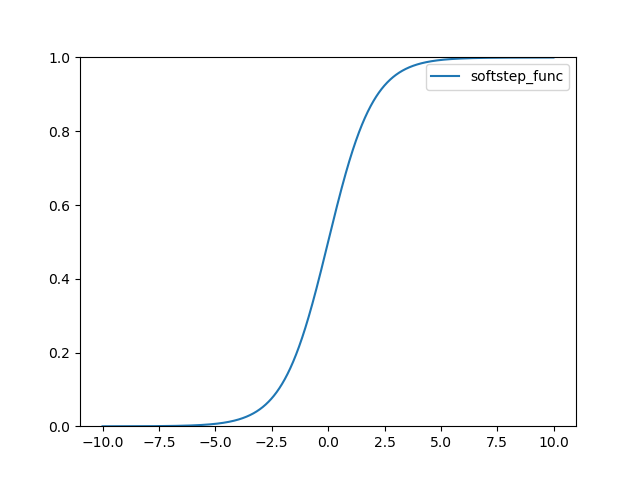
TanH 함수 정의 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def tanh_func(x):
return np.tanh(x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, tanh_func(x), linestyle='-', label="tanh_func")
plt.ylim(-1, 1)
plt.legend()
plt.show()
그래프는 다음과 같다.
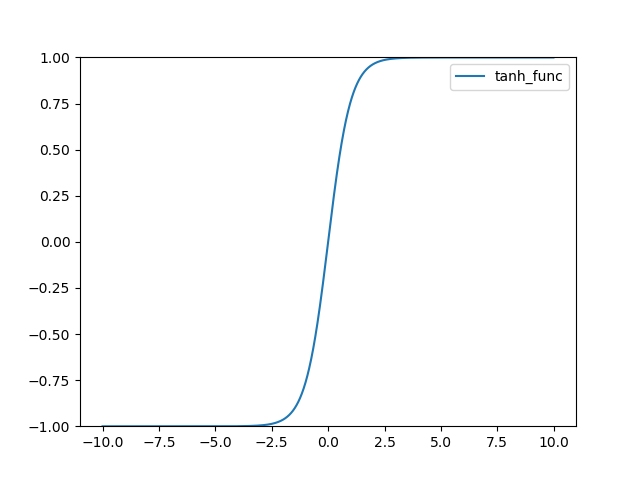
ArcTan 함수 정의는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def arctan_func(x):
return np.arctan(x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, arctan_func(x), linestyle='-', label="arctan_func")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.show()
그래프는 다음과 같다.
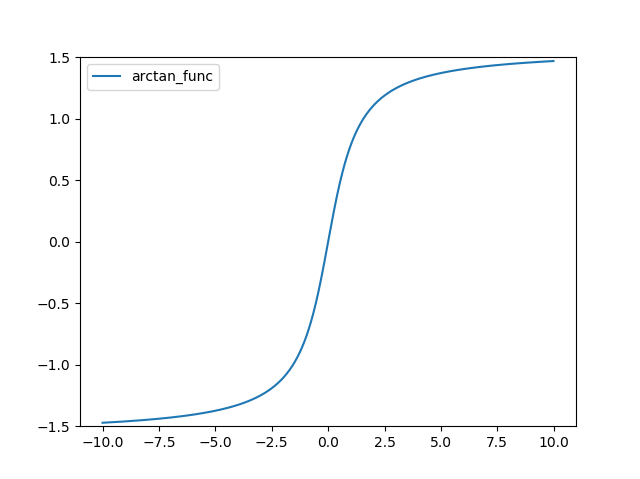
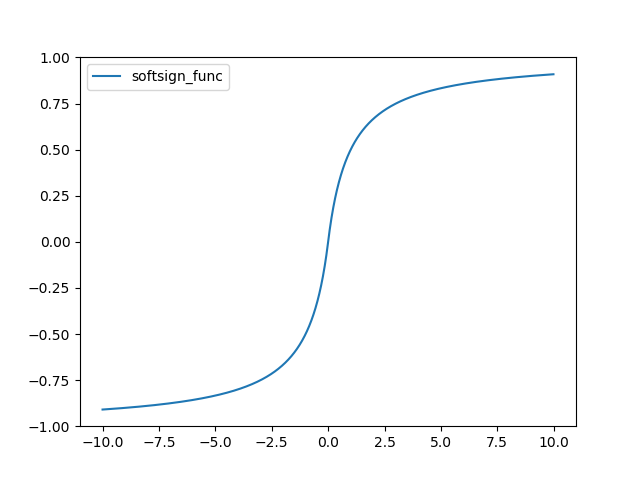
Soft Sign 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softsign_func(x):
return x / ( 1+ np.abs(x) )
x = np.arange(-10, 10, 0.01)
plt.plot(x, softsign_func(x), linestyle='-', label="softsign_func")
plt.ylim(-1, 1)
plt.legend()
plt.show()
그래프는 다음과 같다.
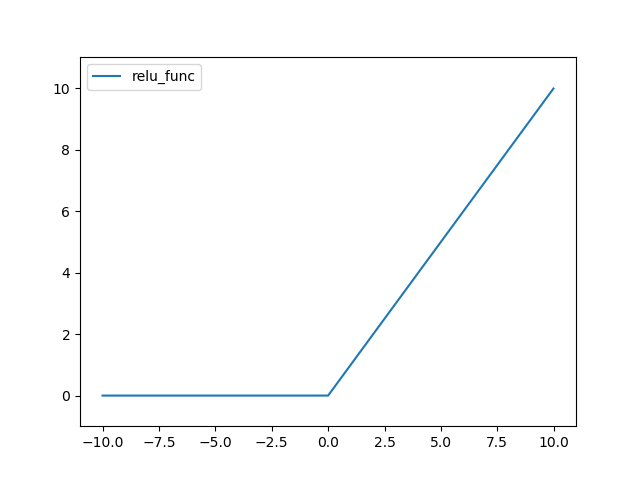
ReLU(Rectified Linear Unit) 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def relu_func(x):
return (x>0)*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, relu_func(x), linestyle='-', label="relu_func")
plt.ylim(-1, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
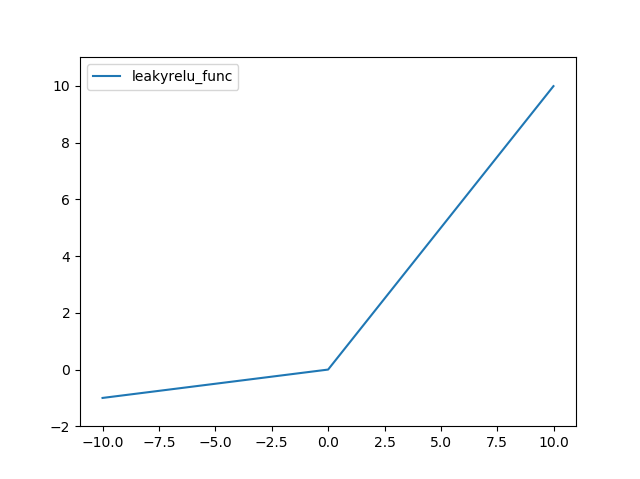
Leaky ReLU 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def leakyrelu_func(x, alpha=0.1):
return (x>=0)*x + (x<0)*alpha*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, leakyrelu_func(x), linestyle='-', label="leakyrelu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
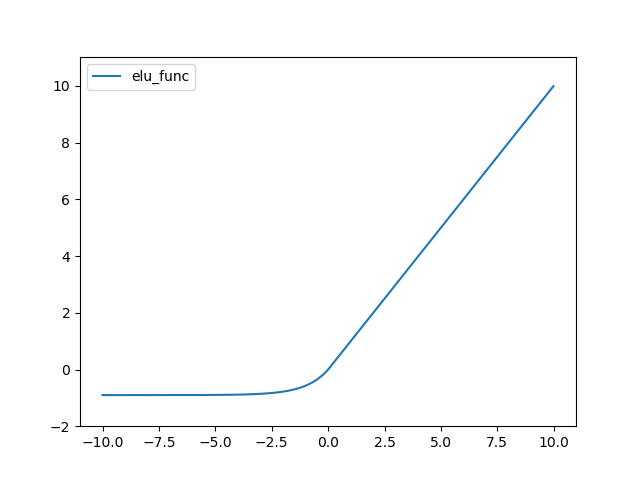
ELU(Exponential Linear Unit) 함수는 다음과 같다.
def elu_func(x, alpha=0.9):
return (x>=0)*x + (x<0)*alpha*(np.exp(x)-1)
x = np.arange(-10, 10, 0.01)
plt.plot(x, elu_func(x), linestyle='-', label="elu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
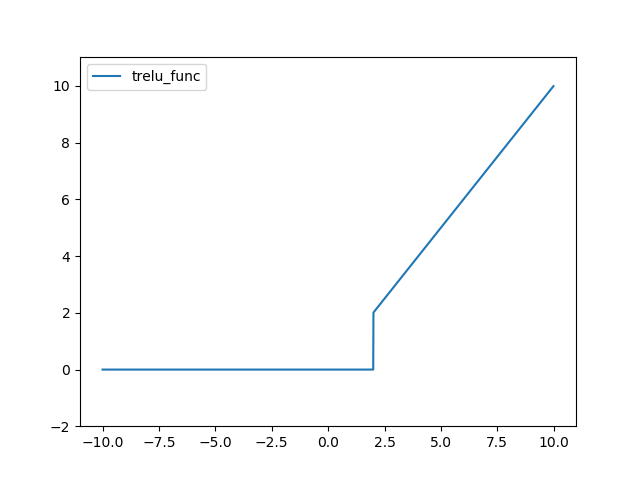
TreLU 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def trelu_func(x, thres=2):
return (x>thres)*x
x = np.arange(-10, 10, 0.01)
plt.plot(x, trelu_func(x), linestyle='-', label="trelu_func")
plt.ylim(-2, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
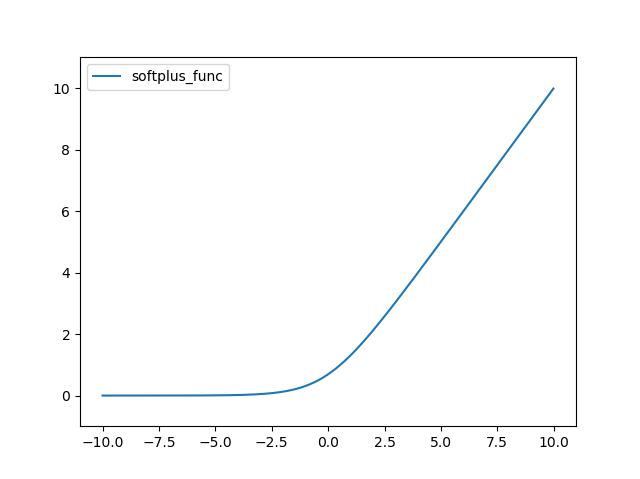
SoftPlus 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def softplus_func(x):
return np.log( 1 + np.exp(x) )
x = np.arange(-10, 10, 0.01)
plt.plot(x, softplus_func(x), linestyle='-', label="softplus_func")
plt.ylim(-1, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
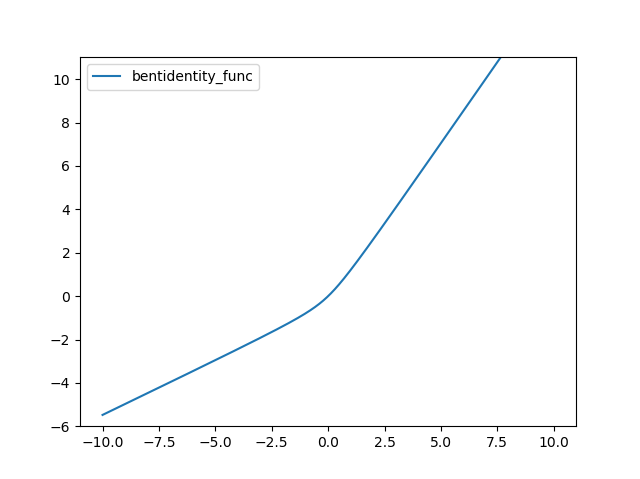
Bent identity 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def bentidentity_func(x):
return (np.sqrt(x*x+1)-1)/2+x
x = np.arange(-10, 10, 0.01)
plt.plot(x, bentidentity_func(x), linestyle='-', label="bentidentity_func")
plt.ylim(-6, 11)
plt.legend()
plt.show()
결과는 다음과 같다.
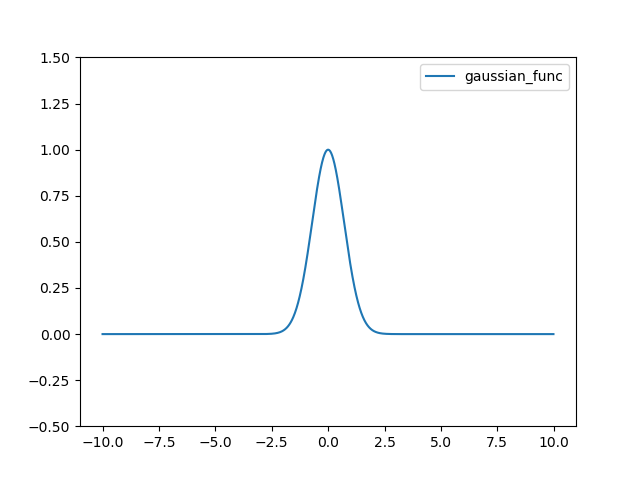
Gaussian 함수는 다음과 같다.
import numpy as np
import matplotlib.pylab as plt
def gaussian_func(x):
return np.exp(-x*x)
x = np.arange(-10, 10, 0.01)
plt.plot(x, gaussian_func(x), linestyle='-', label="gaussian_func")
plt.ylim(-0.5, 1.5)
plt.legend()
plt.show()
결과는 다음과 같다.