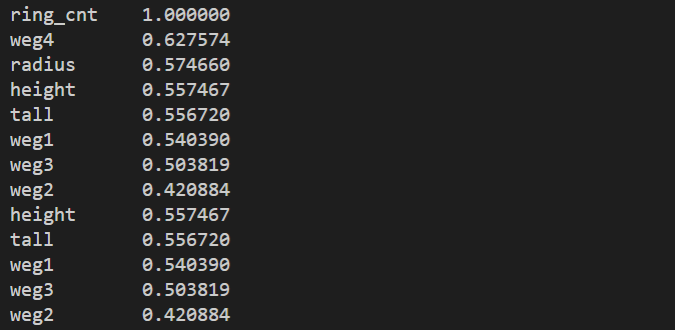
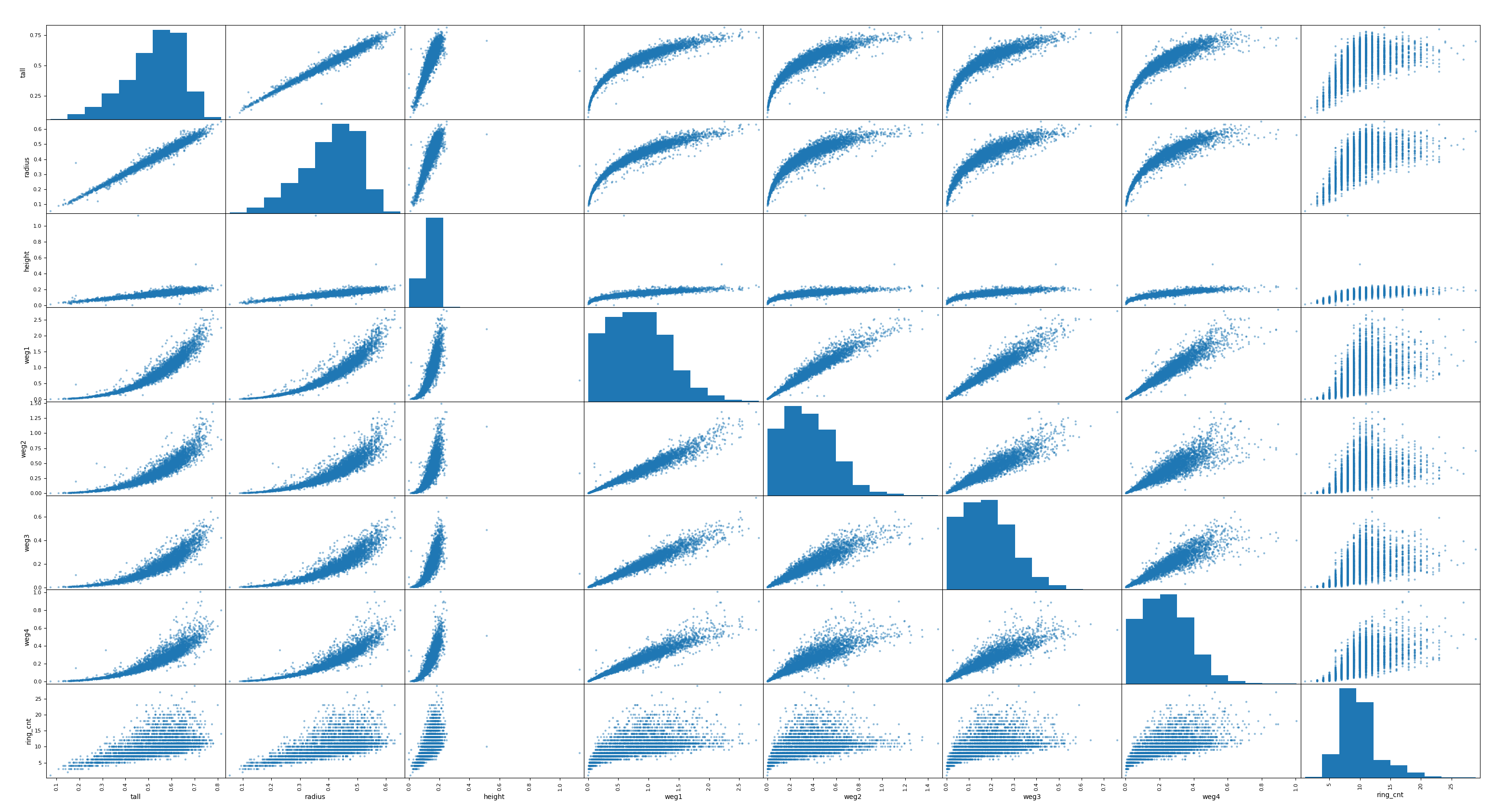
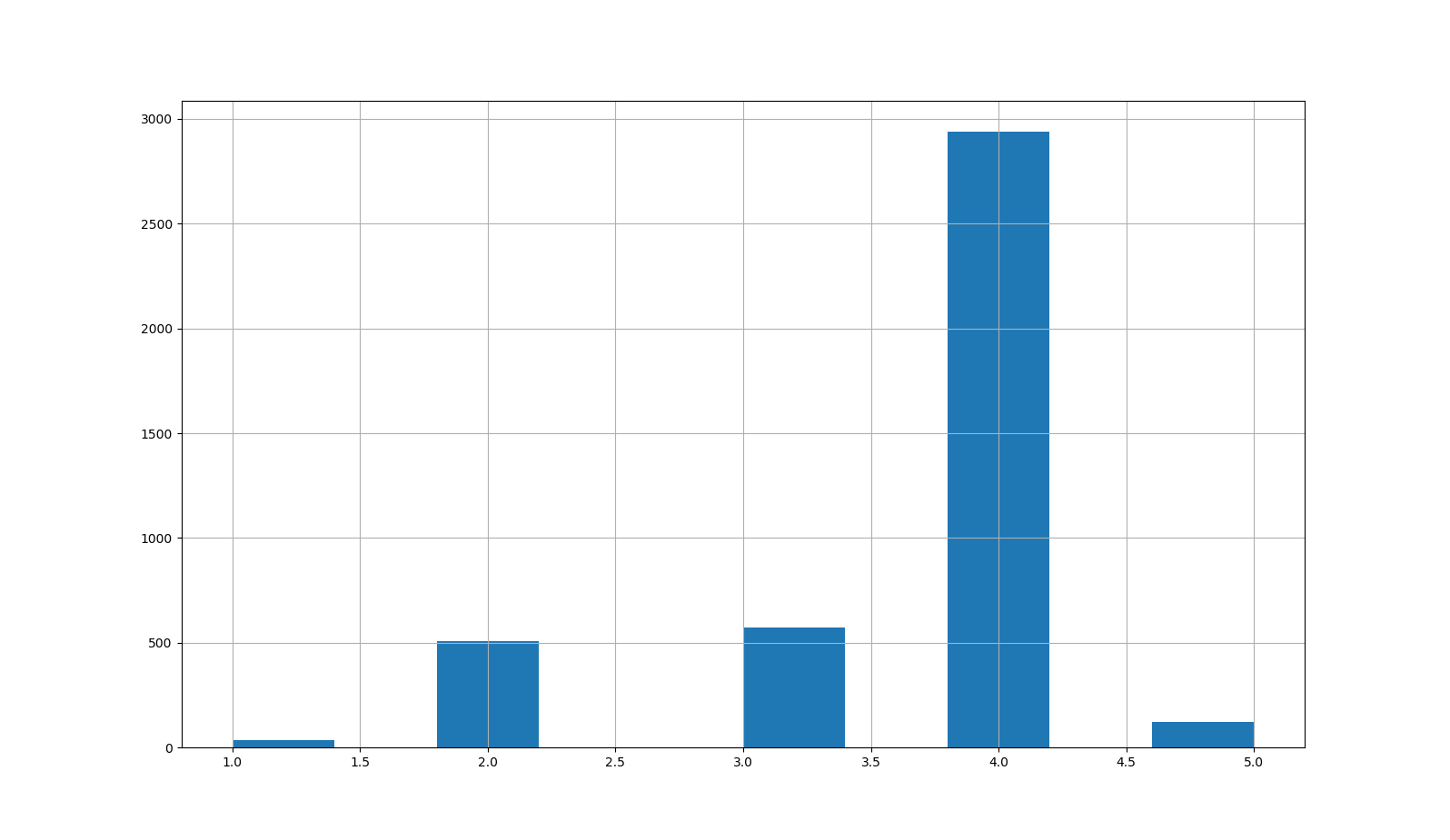
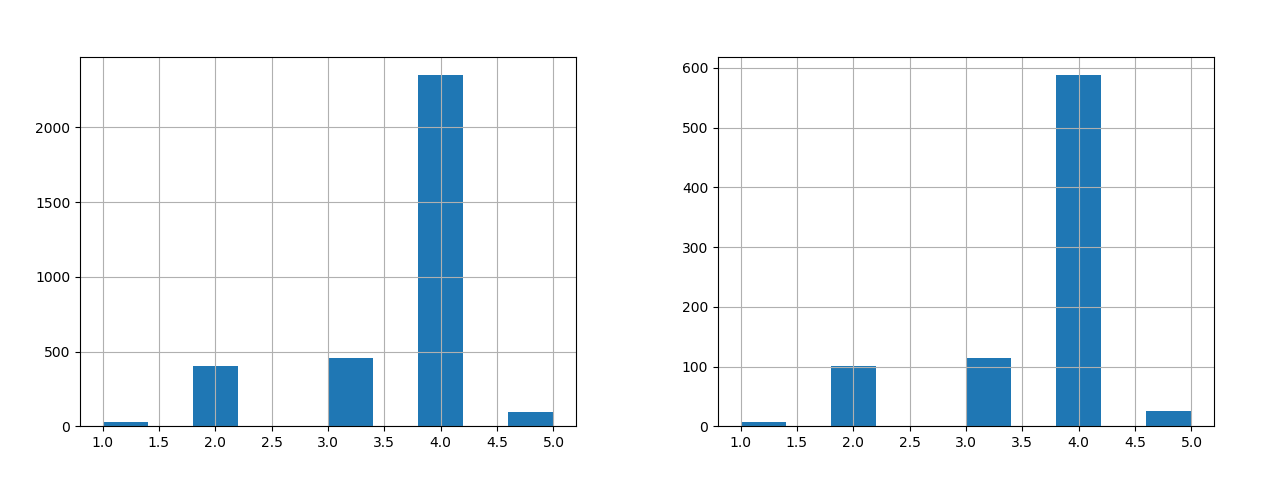
회귀분석은 다수의 특징값을 입력으로 하나의 특징값(실수값)을 산출하는 것입니다. 세가지 방법이 있는데, 선형회귀(Linear Regression)과 의사결정트리(Decision Tree) 그리고 렌덤 포레스트(Random Forest)입니다. 하나의 주제를 정하고 이 3가지 방법을 통해 회귀분석을 테스트해 보도록 하겠습니다. 이 글에서 적용한 회귀 분석 주제는 전복의 나이를 예측하는 것으로 전복의 ‘성별’, ‘키’, ‘지름’, ‘높이’, ‘전체무게’, ‘몸통무게’, ‘내장무게’, ‘껍질무게’를 입력하면 ‘껍질의 고리수’를 예측한 뒤 예측된 ‘껍질의 고리수’에 1.5를 더하면 전복의 나이가 된다고 합니다.
이에 대한 전복의 데이터셋은 kaggle에서 쉽게 다운로드 받을 수 있습니다. 일단 다운로드 받은 데이터셋을 다음과 같은 코드를 통해 전처리하여 특징과 레이블로 구분하고, 학습용과 테스트용으로 구분합니다.
# 데이터 파일 로딩
import pandas as pd
raw_data = pd.read_csv('./datasets/datasets_1495_2672_abalone.data.csv',
names=['sex', 'tall', 'radius', 'height', 'weg1', 'weg2', 'weg3', 'weg4', 'ring_cnt'])
#names=['성별', '키', '지름', '높이', '전체무게', '몸통무게', '내장무게', '껍질무게', '껍질의고리수']
print(raw_data[:7])
# 레이블 분리
data_ring_cnt = raw_data[["ring_cnt"]]
data = raw_data.drop("ring_cnt", axis=1)
# 범주형 특징(sex)에 대한 원핫 인코딩
from sklearn.preprocessing import OneHotEncoder
data_cat = data[["sex"]]
onehot_encoder = OneHotEncoder()
data_cat_onehot = onehot_encoder.fit_transform(data_cat)
print(onehot_encoder.categories_)
# 범주형 특징 제거
data = data.drop("sex", axis=1)
# 범주형 필드가 제거되어 수치형 특징들에 대해 0~1 구간의 크기로 조정
#from sklearn.preprocessing import StandardScaler
#minmax_scaler = StandardScaler()
#data = minmax_scaler.fit_transform(data)
# 원핫인코딩된 범주형 특징과 스케일링된 수치형 특징 및 레이블 결합
import numpy as np
data = np.c_[data_cat_onehot.toarray(), data, data_ring_cnt]
data = pd.DataFrame(data, columns=['sex_F', 'sex_I', 'sex_M', 'sex_''tall', 'radius', 'height', 'weg1', 'weg2', 'weg3', 'weg4', 'ring_cnt'])
print(data[:7])
# 학습 데이터와 테스트 데이터 분리
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(data, test_size=0.1, random_state=47)
# 입력 특징과 레이블의 분리
train_data = train_set.drop("ring_cnt", axis=1)
train_data_label = train_set["ring_cnt"].copy()
test_data = test_set.drop("ring_cnt", axis=1)
test_data_label = test_set["ring_cnt"].copy()
위의 코드는 아래의 글들을 참조하여 파악할 수 있습니다.
다소 험난한 데이터셋의 준비가 끝났으니, 이제 이 글의 본질인 세가지 회귀분석 방식을 하나씩 살펴보겠습니다. 먼저 선형회귀입니다. 참고로 기계학습 과정에 대한 시간 대부분을 차지 하는 작업은 이러한 데이터의 수집과 가공 및 정제이며, 그 다음으로 컴퓨터(GPU)를 통한 모델의 학습입니다. 사람이 관여하는 시간은 상대적으로 매우 적습니다. 물론 모델을 직접 설계하는 경우라면 달라질 수 있겠으나, 역시 데이터 작업과 GPU의 학습 시간은 상대적으로 많이 소요됩니다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(train_data, train_data_label)
from sklearn.metrics import mean_squared_error
some_predicted = model.predict(test_data)
mse = np.sqrt(mean_squared_error(some_predicted, test_data_label))
print('평균제곱근오차', mse)
학습된 모델을 테스트 데이터 셋으로 평가한 오차는 다음과 같습니다.
평균제곱근오차 1.9166262592968584
다음은 의사결정트리 방식입니다.
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(train_data, train_data_label)
from sklearn.metrics import mean_squared_error
some_predicted = model.predict(test_data)
mse = np.sqrt(mean_squared_error(some_predicted, test_data_label))
print('평균제곱근오차', mse)
평균제곱근오차 2.8716565747410656
세번째로 랜덤 포레스트 방식입니다.
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(train_data, train_data_label)
from sklearn.metrics import mean_squared_error
some_predicted = model.predict(test_data)
mse = np.sqrt(mean_squared_error(some_predicted, test_data_label))
print('평균제곱근오차', mse)
평균제곱근오차 2.0828589571564127
마지막으로 SVM(Support Vector Manchine) 방식입니다.
from sklearn import svm model = svm.SVC() model.fit(train_data, train_data_label)
평균제곱근오차 2.537753216441624
이 글의 데이터셋에 대해서는 선형회귀 방식이 가장 오차가 작은 것은 것을 알 수 있습니다. 하지만 이 글에서 테스트한 3가지 모델의 하이퍼파라메터는 기본값을 사용하였습니다. 하이퍼파라메터의 세부 튜팅을 수행하면 결과가 달라질 수 있습니다.