시계열 데이터는 공간 데이터와 마찬가지로 그 의미가 매우 큽니다. 이미 존재하는 많은 데이터는 시간에 따라 축척된다는 점에서 볼때 거의 대부분의 데이터는 시계열성을 갖습니다. 더욱이 공간 데이터와 시계열 데이터가 융합되었을때 그 의미는 더욱 강화됩니다. 시계열 데이터로는 단어들의 순서에 따라 그 의미가 달라지는 문장과 같은 자연어 등이 있습니다. 딥러닝에서 신경망 모델도 중요하지만, 신경망이 유효한 기능 작용을 할 수 있게 만드는 훈련에서 활용되는 데이터셋 중 시계열 데이터를 실제 신경망에 주입시키기 위한 내부적인 구조를 정리해 봅니다.
RNN 신경망에서 사용되는 시계열 데이터를 손쉽게 읽어오기 위해서 PyTorch에서는 torchtext 패키지를 활용합니다. 자연어에 대한 데이터로써 IMDB가 있는데, 이 데이터셋은 영화 리뷰에 대한 텍스트 문장 데이터와 이 리뷰가 긍정적인지 부정적인지를 나타내는 레이블 데이터로 구성됩니다. 텍스트 문장 데이터는 각 영화 리뷰에 대해 하나의 파일로, 레이블 데이터는 폴더명으로 정해집니다.
먼저 아래의 코드는 IMDB를 다운로드 받고, 2개의 데이터셋인 훈련 데이터셋과 시험 데이터셋으로 구성하라는 코드입니다.
import torch from torchtext import data, datasets TEXT = data.Field(sequential=True, batch_first=True, lower=True) LABEL = data.Field(sequential=False, batch_first=True) trainset, testset = datasets.IMDB.splits(TEXT, LABEL)
위의 코드가 실행되면, trainset과 testset이라는 dataset 객체가 생성되는데요. 이 dataset의 구성은 다음과 같이 구성됩니다.
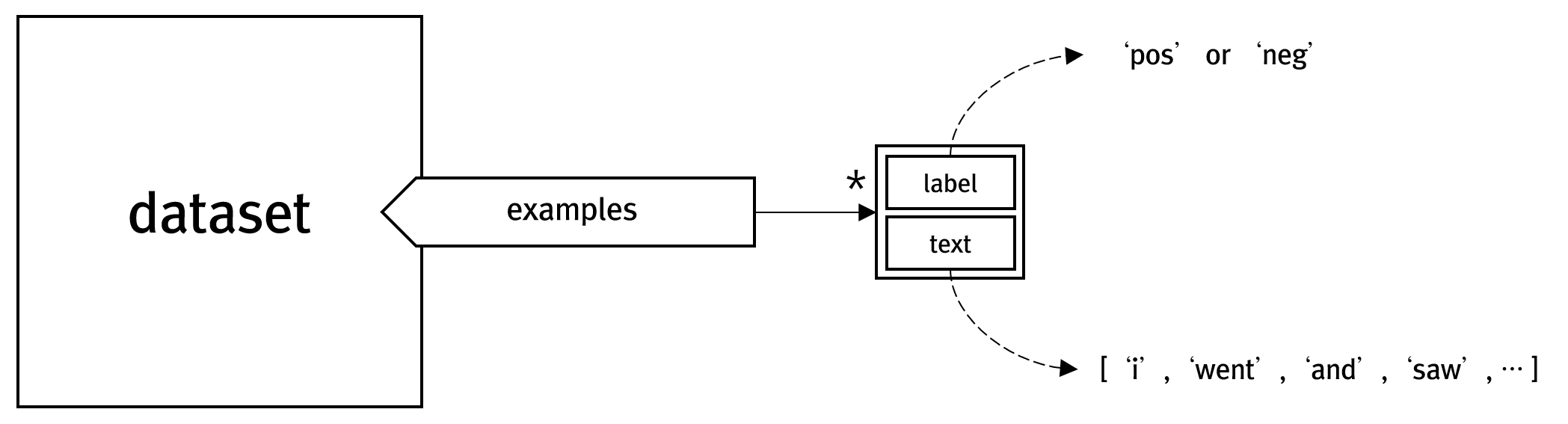
이제 이 데이터셋에 단어 사전을 구성해야 하는데, 이를 위한 코드는 다음과 같습니다.
TEXT.build_vocab(trainset, min_freq=10) LABEL.build_vocab(trainset)
TEXT 필드의 경우 문장중 최소 10번 이상 출현한 단어에 대해서만 사전에 추가하라는 의미에서 min_freq 인자에 10을 지정하고 있습니다. 결국 데이터셋에 다음과 같이 구성됩니다.
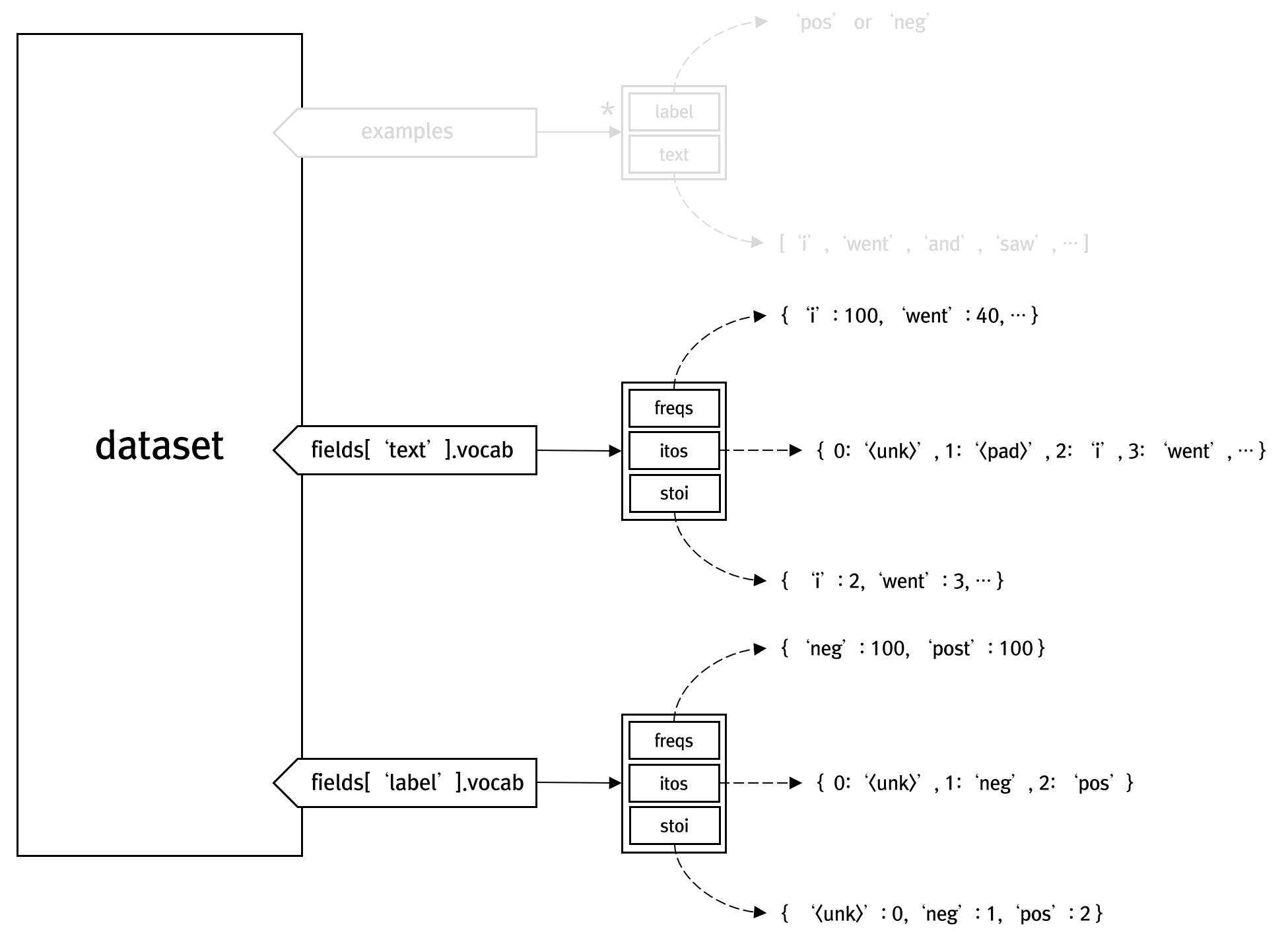
이제 이 데이터셋을 이용해 RNN 신경망의 소중한 입력 데이터를 입력할 수 있게 됩니다. 이를 위해 검증 데이터셋까지 구성하고, 배치단위로 입력 데이터를 구성할 수 있도록 다음 코드가 필요할 것입니다.
trainset, valset = trainset.split(split_ratio=0.8) train_iter, val_iter, test_iter = data.BucketIterator.splits((trainset, valset, testset), batch_size=24, shuffle=True, repeat=False)