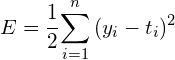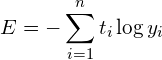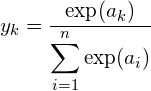머신러닝을 위한 라이브러리 중 파이토치를 이용한 기계학습을 정리해 봅니다. 학습의 주제는 손글씨로 써진 숫자 인식입니다. 먼저 학습을 위한 데이터가 필요한데요. MNIST 데이터를 사용합니다. MNIST는 아래의 그림처럼 테스트 데이터로 60,000개의 손글씨 이미지와 각 이미지에 해당하는 숫자가 무엇인지를 나타내는 60,000개의 라벨값이 있습니다. 또한 이 학습 데이터를 이용해 학습된 모델을 테스트하기 위한 테스트로 손글씨 이미지와 라벨 데이터가 각각 10,000개씩 존재합니다. 이미지 한장의 크기는 28×28 픽셀입니다.

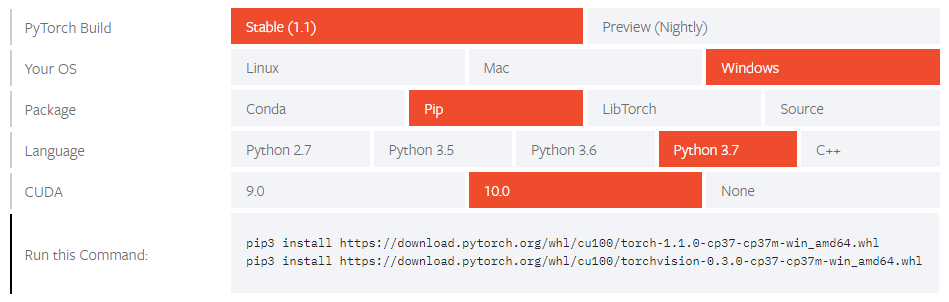
코드는 PyTorch와 MNIST에서 숫자 이미지를 가져오기 위한 라이브러리를 사용하기 위해 아래처럼 import 문으로 시작합니다.
import torch import torchvision
데이터를 통한 훈련을 위해 한번에 60,000개씩 훈련해도 되지만, 학습의 효율과 메모리 사용을 줄이기 위해 Mini-Batch 방식을 이용합니다. 여기서는 미니배치의 크기로 1000을 사용합니다. 그리고 MNIST로부터 훈련 데이터와 테스트 테이터를 다운로드하고 다운로드된 데이터로부터 미니배치만큼 데이터를 로딩하기 위해 다음과 같은 코드를 추가합니다.
batch_size = 1000 mnist_train = torchvision.datasets.MNIST(root="MNIST_data/", train=True, transform=torchvision.transforms.ToTensor(), download=True) mnist_test = torchvision.datasets.MNIST(root="MNIST_data/", train=False, transform=torchvision.transforms.ToTensor(), download=True) data_loader = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, drop_last=True)
머신러닝은 CPU 보다 행렬 연산에 최적화된 GPU를 통해 수행하는 것이 효율적입니다. 즉, Tensor를 GPU에 올려 연산을 수행한다는 의미입니다. 이를 위해 아래의 코드를 추가합니다.
device = torch.device("cuda:0")
이제 손글씨 이미지를 입력하고, 이 이미지가 의미하는 것이 무엇인지를 학습시키기 위한 모델을 정의합니다. 이미지 한장은 28×28 크기이므로 이를 범용적인 입력 데이터로써 받기 위해 각 화소값을 입력값으로 합니다. 즉, 입력값은 28×28인 784개이고, 출력값은 해당 이미지가 어떤 숫자인지에 대한 0~9까지의 확률값이므로 총 10 개입니다. 이를 위한 신경망 모델을 아래처럼 정의합니다. 아래의 코드가 신경망 모델에 대한 구성 코드입니다. 참고로 여기서 사용하는 신경망은 입력층과 출력층으로만 구성되므로 매우 단순합니다. bias=True라는 것은 가중치 외에도 편향값도 사용한다는 의미입니다.
linear = torch.nn.Linear(784, 10, bias=True).to(device)
각 훈련은 손실값만큼 가중치와 편향값을 최적의 값으로 보정하게 됩니다. 이때 손실값으로 Cross Entroy Error를 사용합니다. 이와 함께 출력층에서는 사용하는 활성화함수로는 Softmax 함수를 사용합니다. 파이토치에서는 이를 위해 torch.nn.CrossEntropyLoss를 제공하는데, 이 클래스는 내부적으로 Softmax와 Cross Entroy Error 둘 다 적용해 줍니다. 그리고 훈련에 대한 손실값을 최소화하기 위해 최적의 가중치와 편향값을 찾기 위해 경사하강법을 사용하는데, Hyper-Parameter인 학습율을 0.1로 정했습니다. 이에 대한 코드는 다음과 같습니다.
loss = torch.nn.CrossEntropyLoss().to(device) SDG = torch.optim.SGD(linear.parameters(), lr=0.1)
아래는 1 Epoch(미니배치로 전체 훈련 데이터 처리 단위)에서 몇번의 미니배치가 반복되는지, 그리고 몇번의 Epoch 만큼 훈련할 것인지에 대한 각각의 변수에 대한 코드입니다.
total_batch = len(data_loader) # 60 = 60000 / 1000 (total / batch_size) training_epochs = 10
아래는 훈련에 대한 코드입니다.
for epoch in range(training_epochs):
total_cost = 0
for X, Y in data_loader:
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
hypothesis = linear(X)
cost = loss(hypothesis, Y)
SDG.zero_grad()
cost.backward()
SDG.step()
total_cost += cost
avg_cost = total_cost / total_batch
print("Epoch:", "%03d" % (epoch+1), "cost =", "{:.9f}".format(avg_cost))
위의 코드에서 5번은 (1000, 1, 28, 28) 크기의 텐서를 (1000, 784) 크기의 텐서로 변경해 줍니다. 6번 코드는 이미지 데이터에 대한 라벨값인데, One-Hot 인코딩이 아닌 0~9까지의 값으로 이미지에 대한 의미를 나타냅니다. 8번과 9번은 각각 입력 이미지에 대한 추정값을 얻고, 추정값과 라벨값인 참값 사이의 오차값을 계산합니다. 11번~13번은 오차역전파기법을 이용하여 가중치와 편향값을 보정하는 코드입니다. 18번은 1 에폭마다 손실값이 얼마나 나오는지를 확인하게 되는데, 옳바른 학습이라면 이 손실값은 큰 그림에서 봤을때 점차적으로 줄어들어야 합니다. 아래는 이러한 손실값을 에폭의 반복에 대해 표현한 그래프입니다.
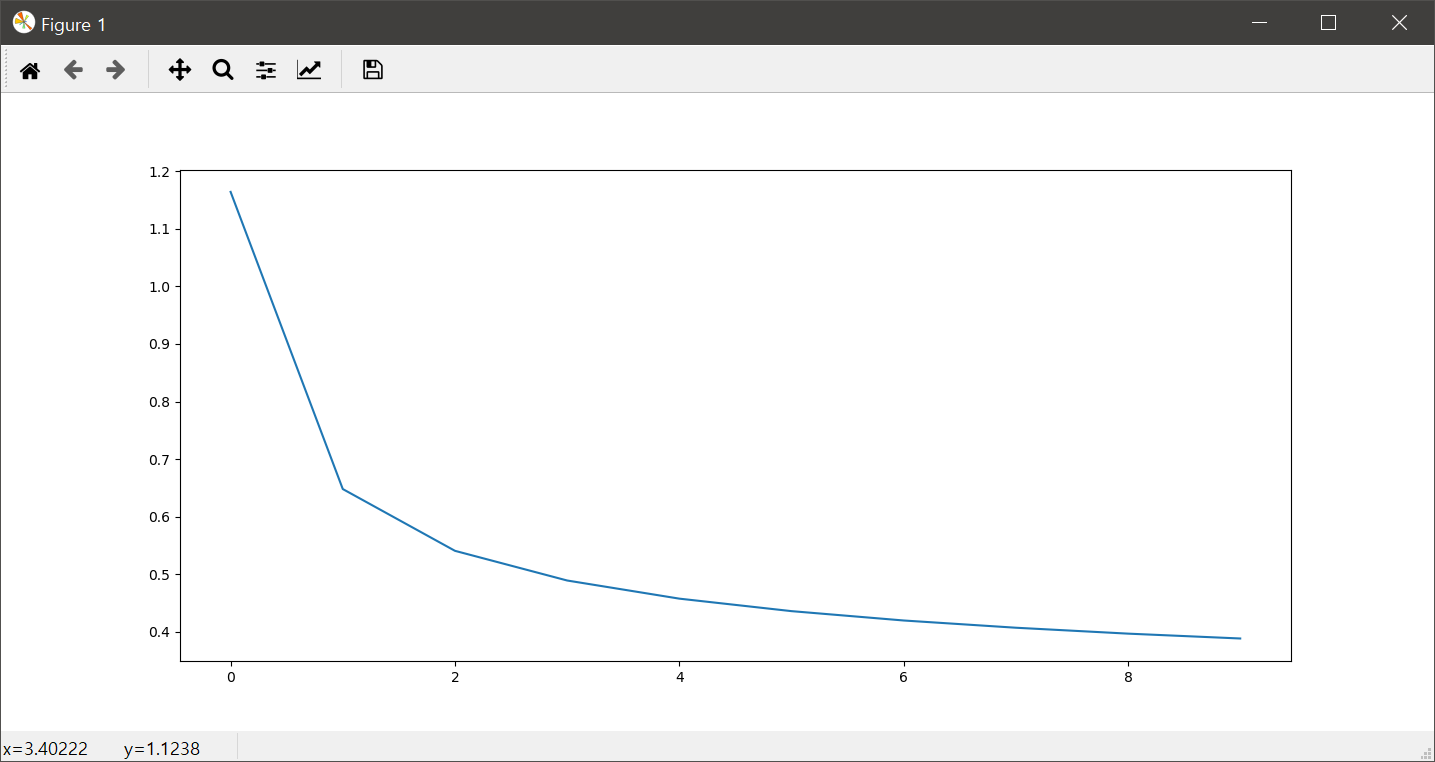
마지막으로 아래의 코드는 위의 훈련을 통해 얻어진 가중치값과 편향값을 테스트 데이터에 적용해 얼마만큼의 정확도가 나오는지 확인하는 코드입니다.
with torch.no_grad():
X_test = mnist_test.data.view(-1, 28 * 28).float().to(device)
Y_test = mnist_test.targets.to(device)
prediction = linear(X_test)
correct_prediction = torch.argmax(prediction, 1) == Y_test
accuracy = correct_prediction.float().mean()
print("Accuracy: ", accuracy.item())
실제 이 코드를 통해 학습해 보면 대략 90% 정도의 정확도를 얻을 수 있습니다. 높은 정확도라고 할수는 없지만, 단순이 이미지의 화소값을 특징으로 일렬로 구성한, 즉 이미지라는 2차원적인 개념을 전혀 고려하지 않고 얻은 정확도라는 점에서 상당이 인상적인데요. 하지만 90%라는 정확도를 개선하기 위해 이미지라는 2차원적인 개념까지 고려하고 반영한 CNN을 이용하면 정확도를 99% 이상으로 올릴 수 있게 됩니다. 99%의 정확도는 인간의 평균 정확도를 넘어선 값입니다.