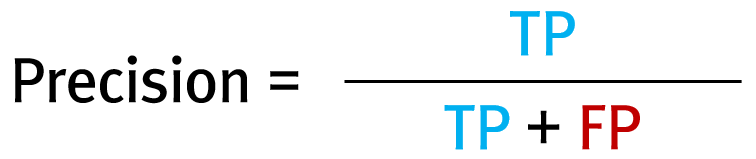처음 딥러닝을 테스트 하기 위해 흔히 사용하는 데이터는 MNIST 입니다. 0~9까지의 손글씨에 대한 28×28 크기의 이미지입니다. 이미지 데이터와 함께 라벨 데이터도 제공되므로 바로 활용할 수 있는 데이터입니다. MNSIT에 영감을 받은 Fashion-MNIST라는 데이터가 존재합니다. 총 10가지의 패션 아이템에 대한 이미지와 라벨입니다. 제공되는 이미지의 예는 아래와 같습니다.

위 이미지들에서 상단부터 3개의 Rows씩을 한 그룹으로 묶으면 각각의 그룹이 의미하는 것은 아래의 표와 그 항목의 순서가 같습니다.
| Label |
Description |
| 0 |
T-shirt/top |
| 1 |
Trouser |
| 2 |
Pullover |
| 3 |
Dress |
| 4 |
Coat |
| 5 |
Sandal |
| 6 |
Shirt |
| 7 |
Sneaker |
| 8 |
Bag |
| 9 |
Ankle boot |
훈련을 위한 이미지와 라벨의 수는 각각 60,000개, 시험을 위한 이미지와 라벨의 수는 각각 10,000개입니다. 이 글은 Fashion-MNIST를 PyTorch를 이용해 훈련을 시켜보는 코드와 그 결과에 대한 설명입니다.
먼저 필요한 라이브러리를 import 합니다.
import torch
import torch.nn as nn
import torchvision.datasets as dset
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
from torch.utils.data import DataLoader
하이퍼 파라메터는 다음과 같습니다.
batch_size = 100
num_epochs = 250
learning_rate = 0.0001
훈련에 필요한 데이터와 시험에 필요한 데이터를 다운로드 받아야 하는데, PyTorch에서는 이를 위한 도구를 지원하므로, 이를 활용하여 다음 코드처럼 MNIST_Fashion 폴더에 데이터를 다운받고 데이터를 활용할 준비를 합니다.
root = './MNIST_Fashion'
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize(mean=(0.5,), std=(0.5,))])
train_data = dset.FashionMNIST(root=root, train=True, transform=transform, download=True)
test_data = dset.FashionMNIST(root=root, train=False, transform=transform, download=True)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True, drop_last=True)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size, shuffle=False, drop_last=True)
이제 모델을 정의(아래 코드의 4번 코드인 DNN 클래스의 __init__ 함수)하고 사용할 손실함수(아래의 37번 코드)와 최소의 손실값을 가지는 가중치와 편향값을 찾기 위해 방법(아래의 38번 코드) 및 맨 처음 가중치(아래의 30번 weights_init 코드와 35번 코드)를 초기화합니다.
device = torch.device(device + ":0")
class DNN(nn.Module):
def __init__(self):
super(DNN, self).__init__()
self.layer1 = nn.Sequential(
torch.nn.Linear(784, 256, bias=True),
torch.nn.BatchNorm1d(256),
torch.nn.ReLU()
)
self.layer2 = nn.Sequential(
torch.nn.Linear(256, 64, bias=True),
torch.nn.BatchNorm1d(64),
torch.nn.ReLU()
)
self.layer3 = nn.Sequential(
torch.nn.Linear(64, 10, bias=True)
)
def forward(self, x):
x = x.view(x.size(0), -1) # flatten
x_out = self.layer1(x)
x_out = self.layer2(x_out)
x_out = self.layer3(x_out)
return x_out
def weights_init(m):
if isinstance(m, nn.Linear):
nn.init.xavier_normal_(m.weight)
model = DNN().to(device)
model.apply(weights_init)
criterion = torch.nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
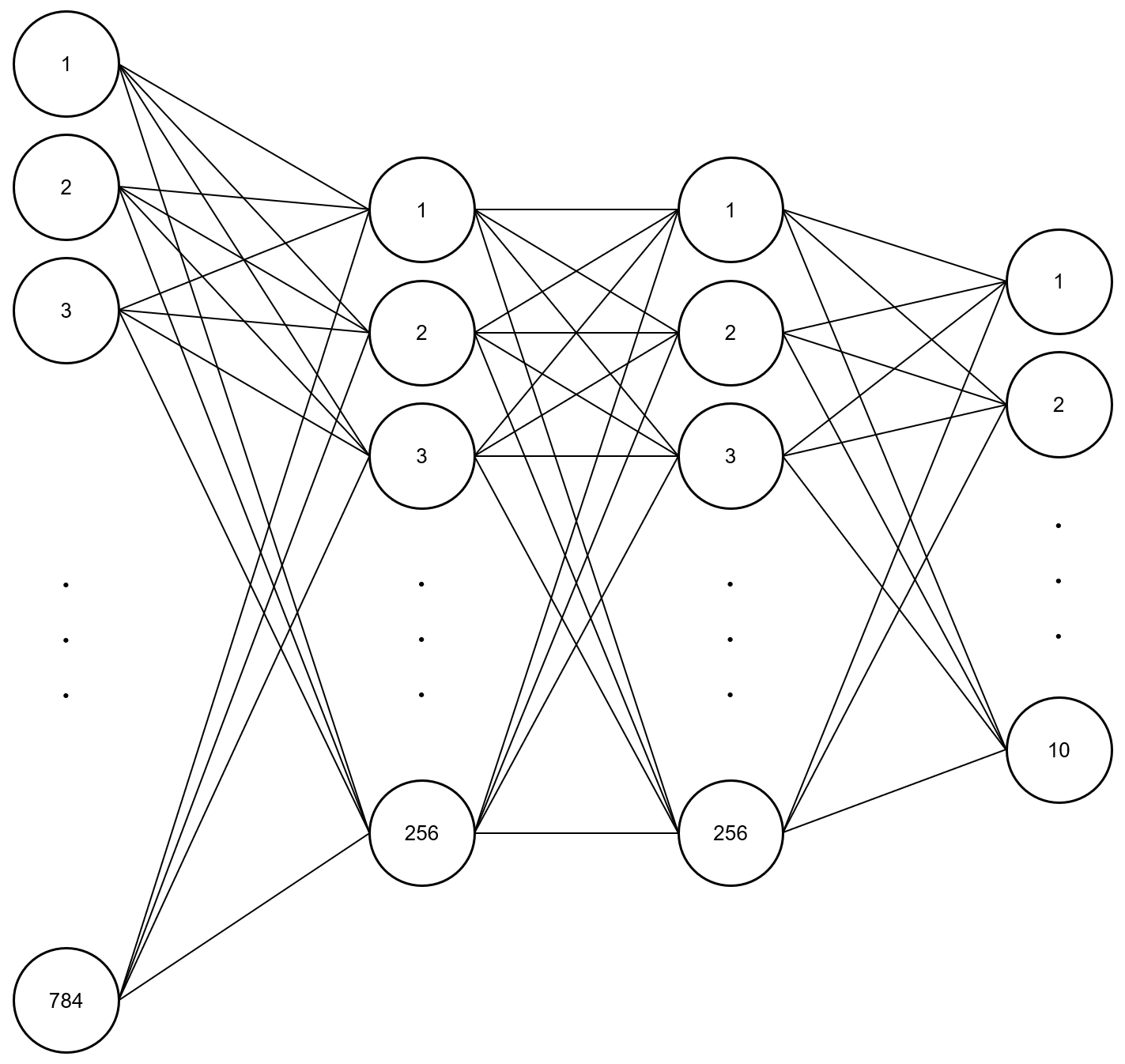
위에서 사용한 모델은 DNN(Deep Neural Network)으로써 다음과 같습니다.
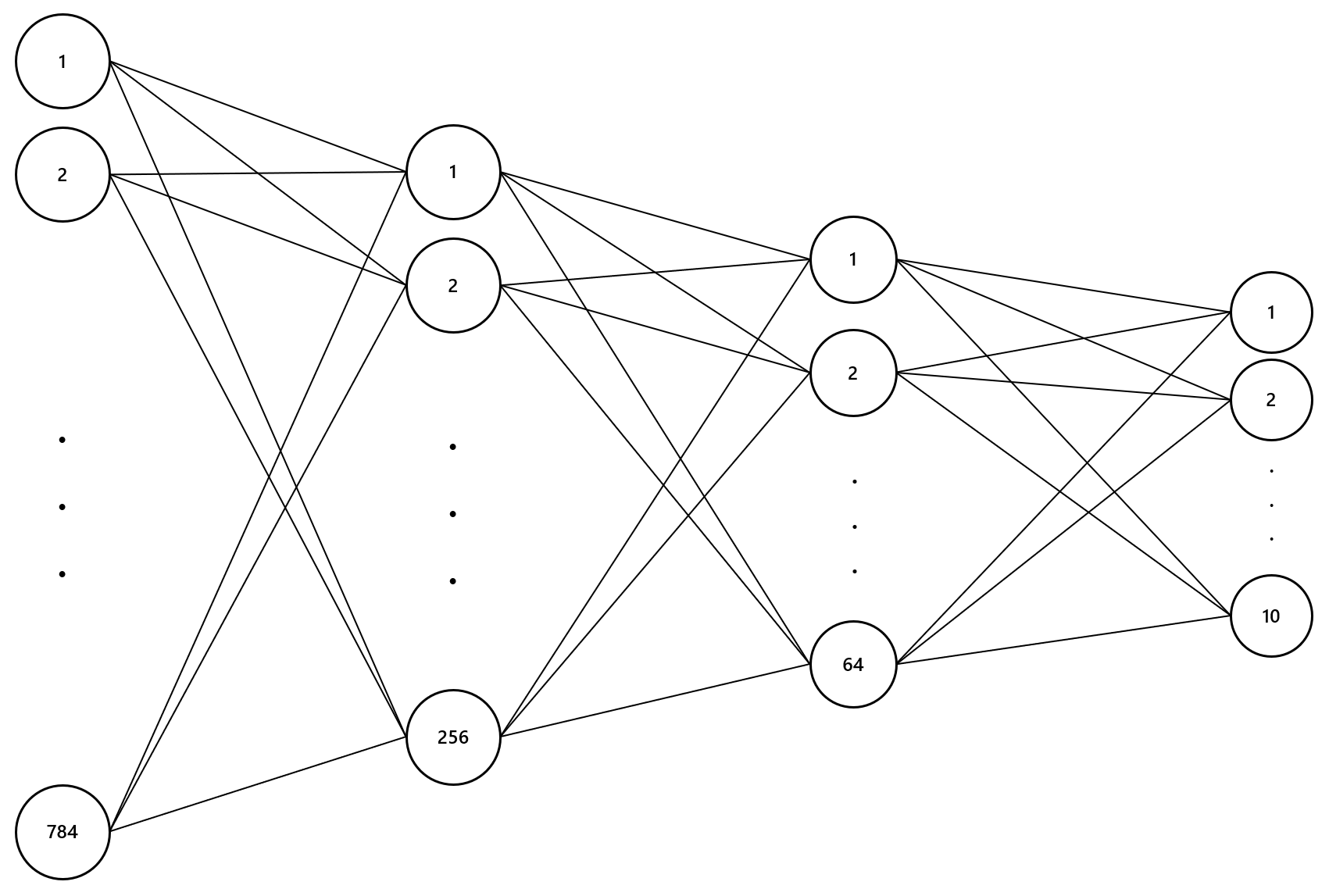
다음은 훈련(Train)에 대한 코드입니다.
costs = []
total_batch = len(train_loader)
for epoch in range(num_epochs):
total_cost = 0
for i, (imgs, labels) in enumerate(train_loader):
imgs, labels = imgs.to(device), labels.to(device)
outputs = model(imgs)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_cost += loss
avg_cost = total_cost / total_batch
print("Epoch:", "%03d" % (epoch+1), "Cost =", "{:.9f}".format(avg_cost))
costs.append(avg_cost)
옳바르게 학습이 된다면 에폭이 증가될때마다 손실값은 점점 줄어 들게 되는데, X축이 에폭, Y축이 손실(비용)인 아래의 그래프의 결과를 도출했습니다.
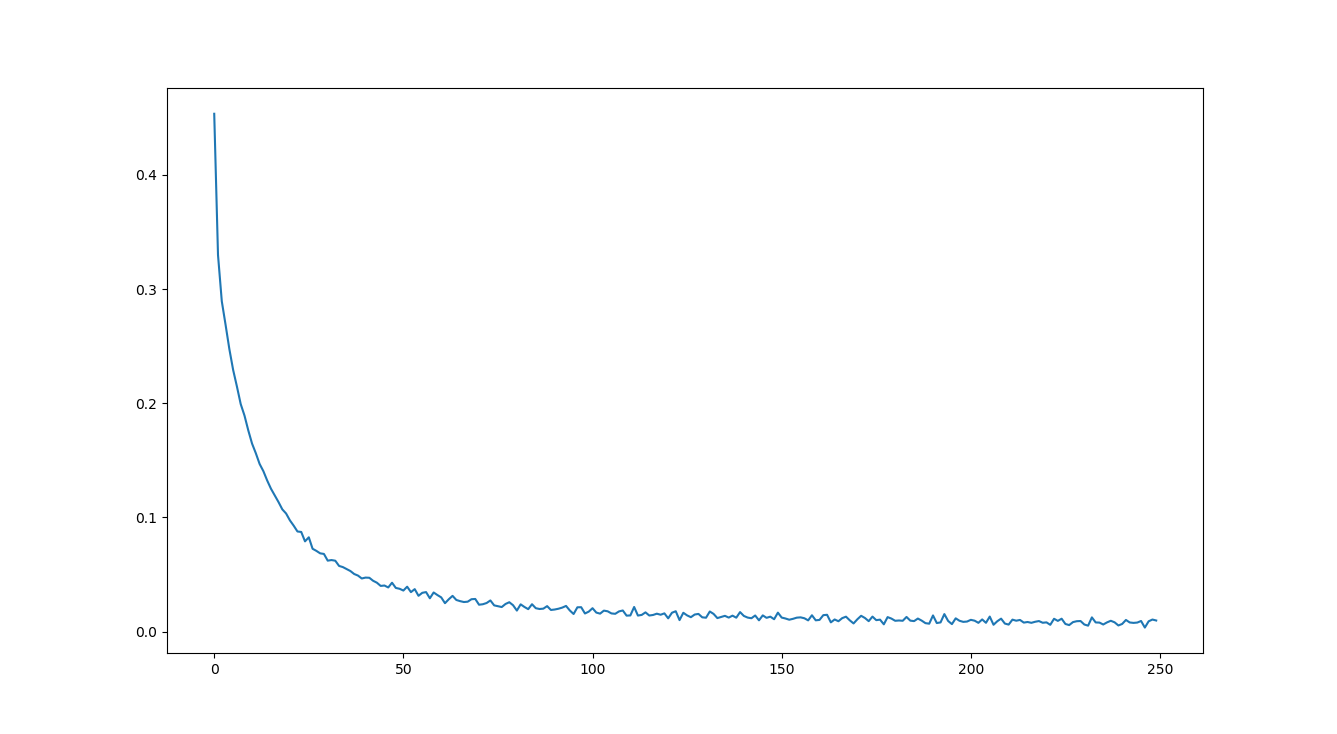
이제 학습된 가중치와 편향값을 통해 테스트를 하는 코드는 아래와 같습니다.
model.eval()
with torch.no_grad():
correct = 0
total = 0
for i, (imgs, labels) in enumerate(test_loader):
imgs, labels = imgs.to(device), labels.to(device)
outputs = model(imgs)
_, argmax = torch.max(outputs, 1)
total += imgs.size(0)
correct += (labels == argmax).sum().item()
print('Accuracy for {} images: {:.2f}%'.format(total, correct / total * 100))
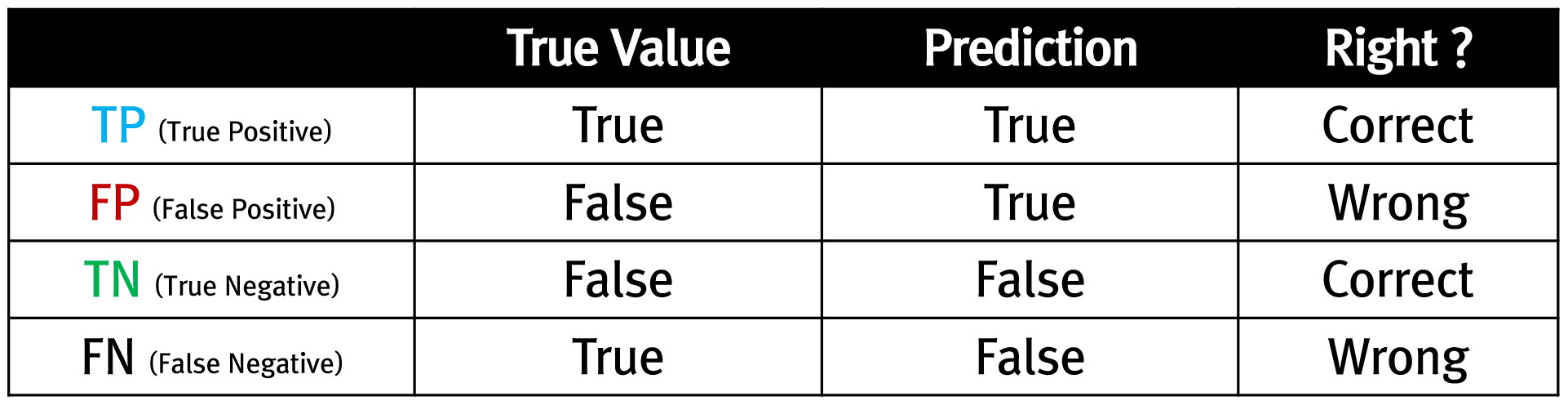
정확도는 89.39%가 도출되었는데요. 이 정확도를 점더 시각적으로 인지하기 위해 테스트 데이터에서 36개의 이미지를 뽑아 각각의 이미지가 어떤 것으로 분류되었는지 확인하는 코드를 작성해 보면 다음과 같습니다.
label_tags = {
0: 'T-Shirt',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle Boot'
}
columns = 6
rows = 6
fig = plt.figure(figsize=(10,10))
model.eval()
for i in range(1, columns*rows+1):
data_idx = np.random.randint(len(test_data))
input_img = test_data[data_idx][0].unsqueeze(dim=0).to(device)
output = model(input_img)
_, argmax = torch.max(output, 1)
pred = label_tags[argmax.item()]
label = label_tags[test_data[data_idx][1]]
fig.add_subplot(rows, columns, i)
if pred == label:
plt.title(pred + ', right !!')
cmap = 'Blues'
else:
plt.title('Not ' + pred + ' but ' + label)
cmap = 'Reds'
plot_img = test_data[data_idx][0][0,:,:]
plt.imshow(plot_img, cmap=cmap)
plt.axis('off')
plt.show()
위의 10번 코드에서 unsqueeze() 함수를 사용한 것은 원본 데이터의 Shape가 (1, 28, 28)인데, 이를 모델에 입력되는 데이터의 Shape인 (1, 1, 28, 28)로 변환해야 하기 때문입니다. 결과는 다음과 같습니다.
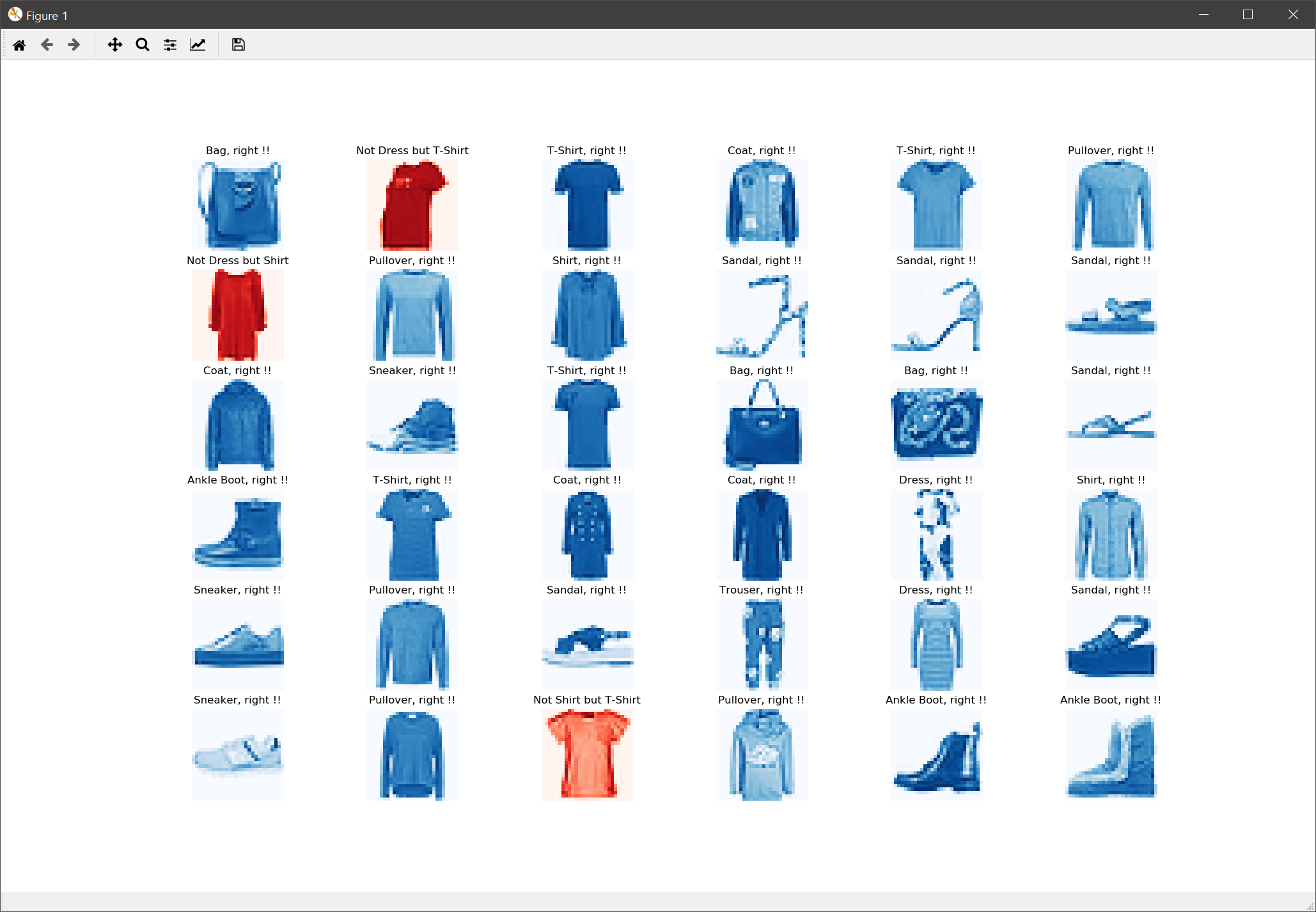
위의 이미지를 보면 분류가 3개 정도 틀린 것으로 표시됩니다. 주로 T셔츠를 그냥 셔츠로 분류하거나 스웨터를 셔츠로 분류한 경우입니다. 이 경우 CNN으로 학습하면 정확도를 더욱 향상시킬 수 있습니다.