k-Means 알고리즘을 이용한 군집화(Cluster)
다음과 같은 데이터가 존재한다고 합시다.
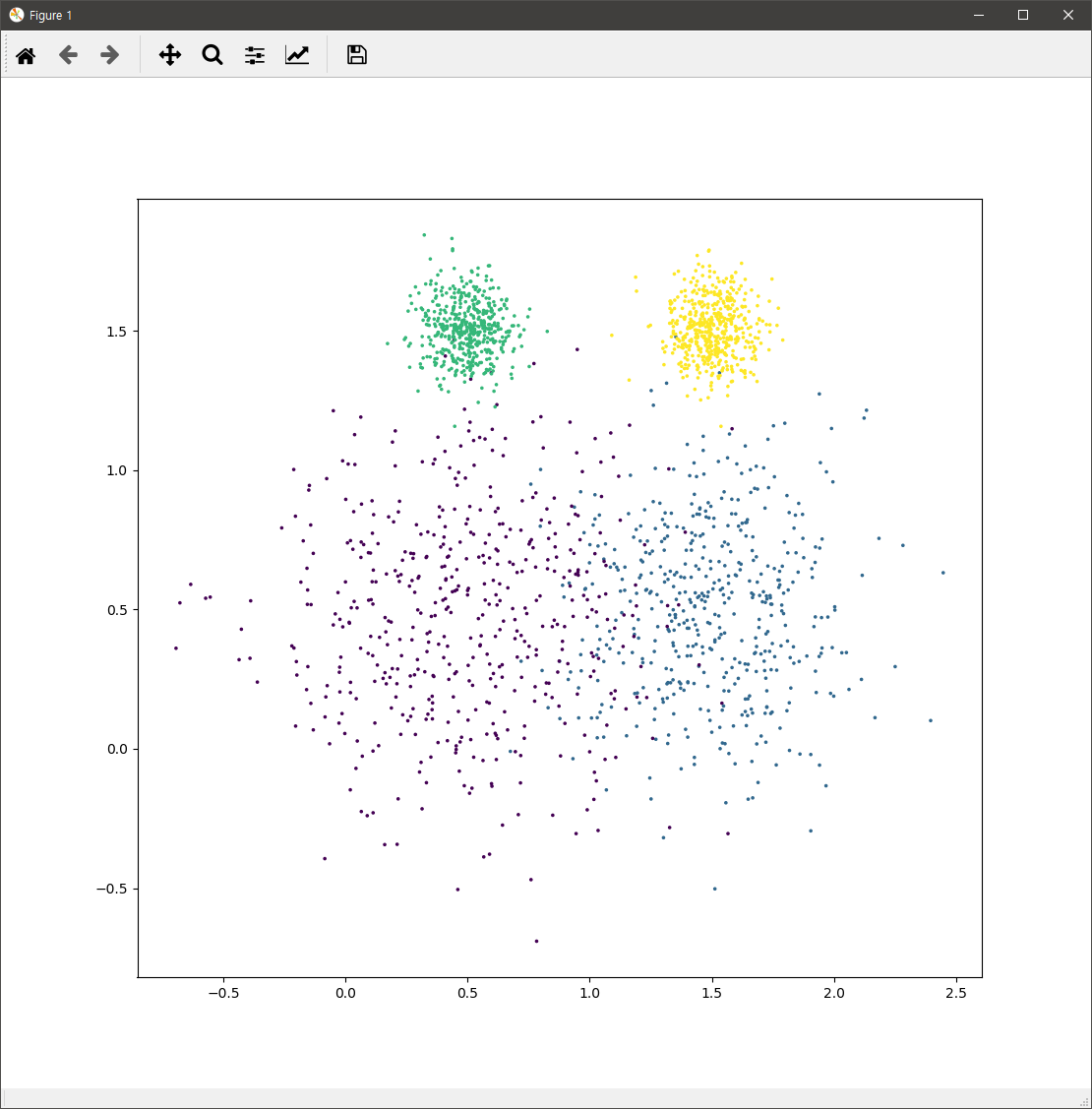
위의 데이터는 아래의 코드로 생성된 것입니다.
import sklearn
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
blob_centers = np.array(
[[ 0.5, 0.5 ],
[ 1.5, 0.5 ],
[ 0.5, 1.5],
[ 1.5, 1.5]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std, random_state=3224)
def plot_data(X, y):
plt.scatter(X[:, 0], X[:, 1], c=y, marker='.', s=10)
plot_data(X, y)
plt.show()
위의 데이터는 4개로 구룹지을 수 있다는 것을 코드를 통해 알 수 있습니다. 이제 이 데이터를 k-Means를 이용하여 4개로 군집화하는 코드는 살펴보면 다음과 같습니다.
k = 4 kmeans = KMeans(n_clusters=k) y_pred = kmeans.fit_predict(X)
위의 코드를 통해 kmeans 모델은 새로운 샘플 데이터에 대해서 4개의 그룹중 어떤 그룹에 포함되는지 예측할 수 있습니다. 이에 대한 시각화 코드는 다음과 같습니다.
def plot_decision_boundaries(clusterer, X, y, resolution=500):
mins = X.min(axis=0) - 0.1
maxs = X.max(axis=0) + 0.1
xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution), np.linspace(mins[1], maxs[1], resolution))
Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), cmap="gist_stern")
plt.contour(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]), linewidths=1, colors='k')
plot_data(X, y)
plot_decision_boundaries(kmeans, X, y)
plt.show()
위 코드의 결과는 다음과 같습니다.
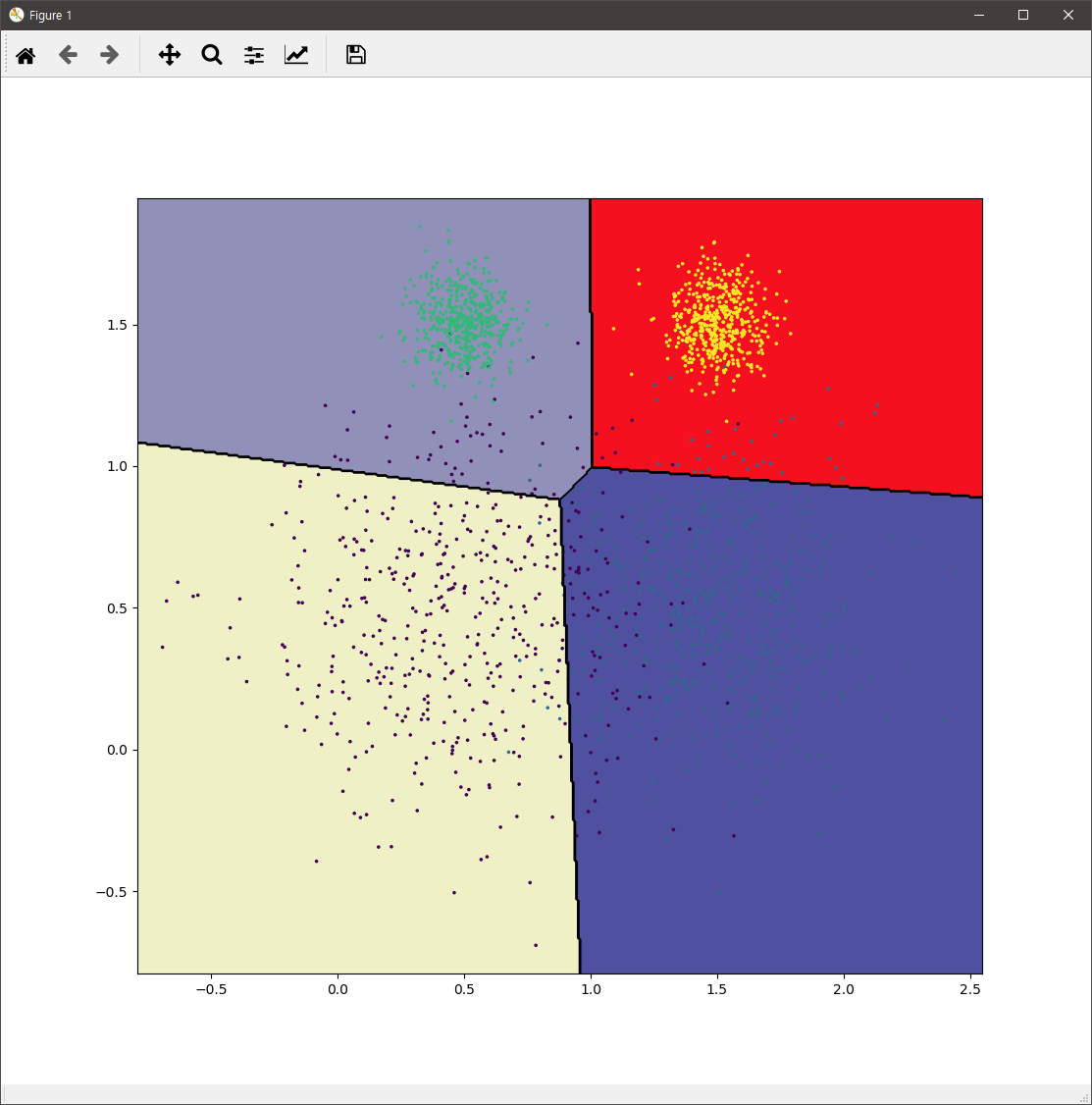
실제 k-means를 적용할 시에는 군집화할 개수를 알 수 없는 경우가 대부분입니다. 위의 코드에서는 k 값인데요. 이 값을 효과적으로 결정하기 위해서는 실루엣 다이어그램(Silhouette Diagram)을 통해 효과적으로 파악할 수 있습니다.
차원 축소
머신러닝으로 풀고자 하는 문제에 대한 입력값, 즉 특성은 그 상황에 따라 몇개에서 수백, 수천만개 이상으로 이루어질 수 있습니다. 그렇다고 이 모든 특성이 문제 해결을 위해 중요한 것은 아닙니다. 어떤 특성은 문제 해결에 미치는 영향이 미미하거나 아예 없는 경우도 있습니다. 이럴때 문제 해결에 미미한 영향을 가지는 특성은 제거하는 것은 해당 문제를 풀 수 있는 가능성을 높여준다는 점에서 매우 의미가 큽니다. 문제 해결의 가능성을 높여지는 것 뿐만이 아니라 불필요한 특성을 줄여줌으로써 학습 속도가 향상되며, 더 적은 학습 데이터만으로도 높은 정확도의 결과를 얻을 수 있습니다. 또한 특성을 2개 또는 3개로 줄임으로써 우리에게 익숙한 2차원과 3차원의 공간에 데이터를 시각화하여 어떤 통찰을 얻을 수도 있습니다.
이 글은 특성수를 줄이는, 즉 차원을 축소하는 방법에 몇가지를 언급합니다. 구체적인 예로 다음과 같은 3개의 특성으로 구성된 3차원의 데이터를 특성 2개인 2차원의 데이터로 축소함에 있어서, 최대한 원래 데이터가 가지고 있는 좋은 특성을 유지하도록 하는데, 이는 통계학적으로는 분석을 최대한 보존하는 방향이기도 합니다. 먼저 특성을 줄일 대상이 되는 원본 데이터를 구성하고 이를 3차원으로 시각화하는 코드는 다음과 같습니다.
from sklearn.datasets import make_swiss_roll import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D X, t = make_swiss_roll(n_samples=500, noise=0.1, random_state=3224) fig = plt.figure(figsize=(6, 5)) ax = fig.add_subplot(111, projection='3d') ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.hot) plt.show()
위 코드의 결과는 다음과 같습니다.
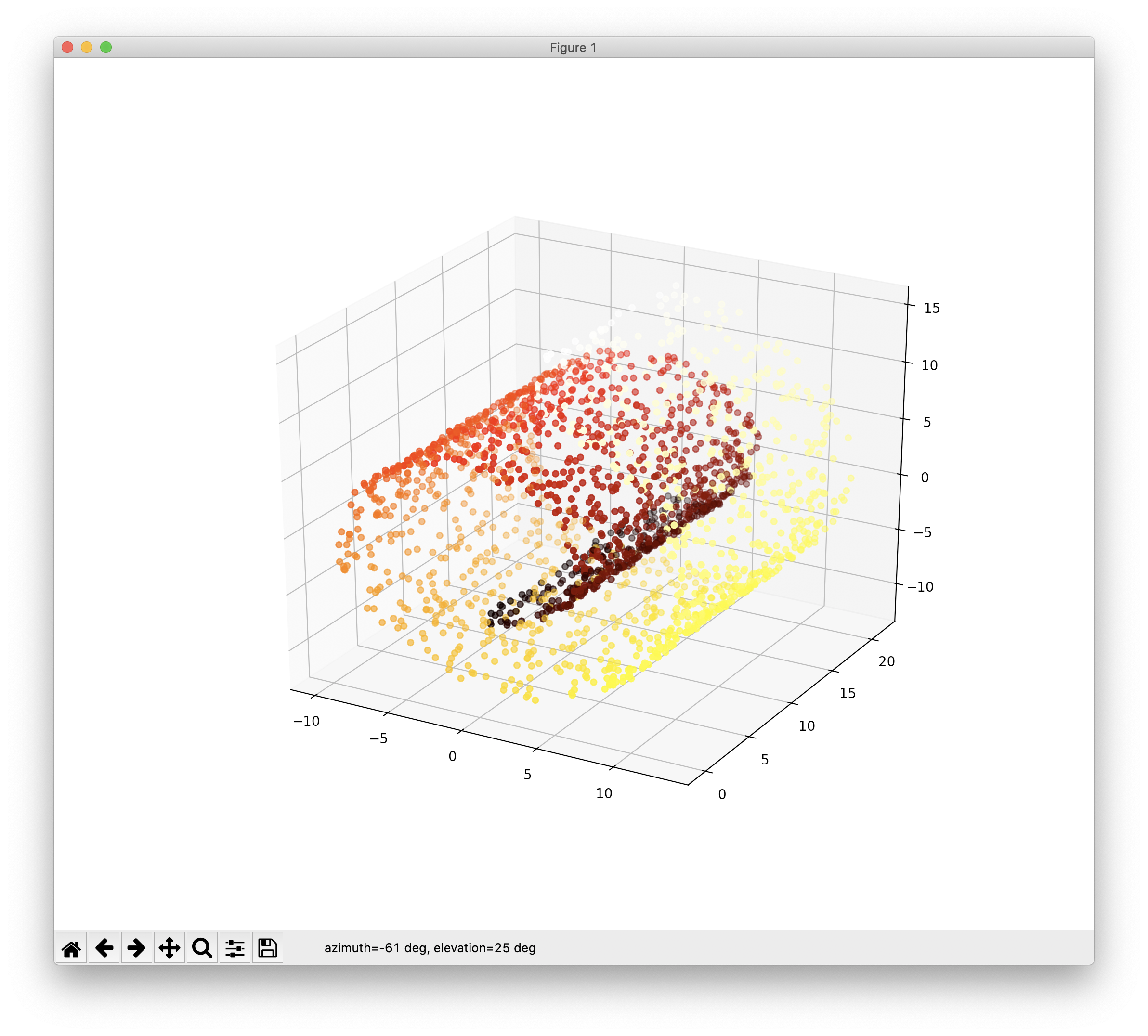
데이터는 사이킷런에서 제공하는 데이터셋 중 스위스롤로 스펀지 케익을 롤케익처럼 둘둘 말아 놓은 형태인데요, 이를 평면으로 펴서 시각화하는 코드와 그 결과는 다음과 같습니다.
plt.scatter(t, X[:, 1], c=t, cmap=plt.cm.hot) plt.show()
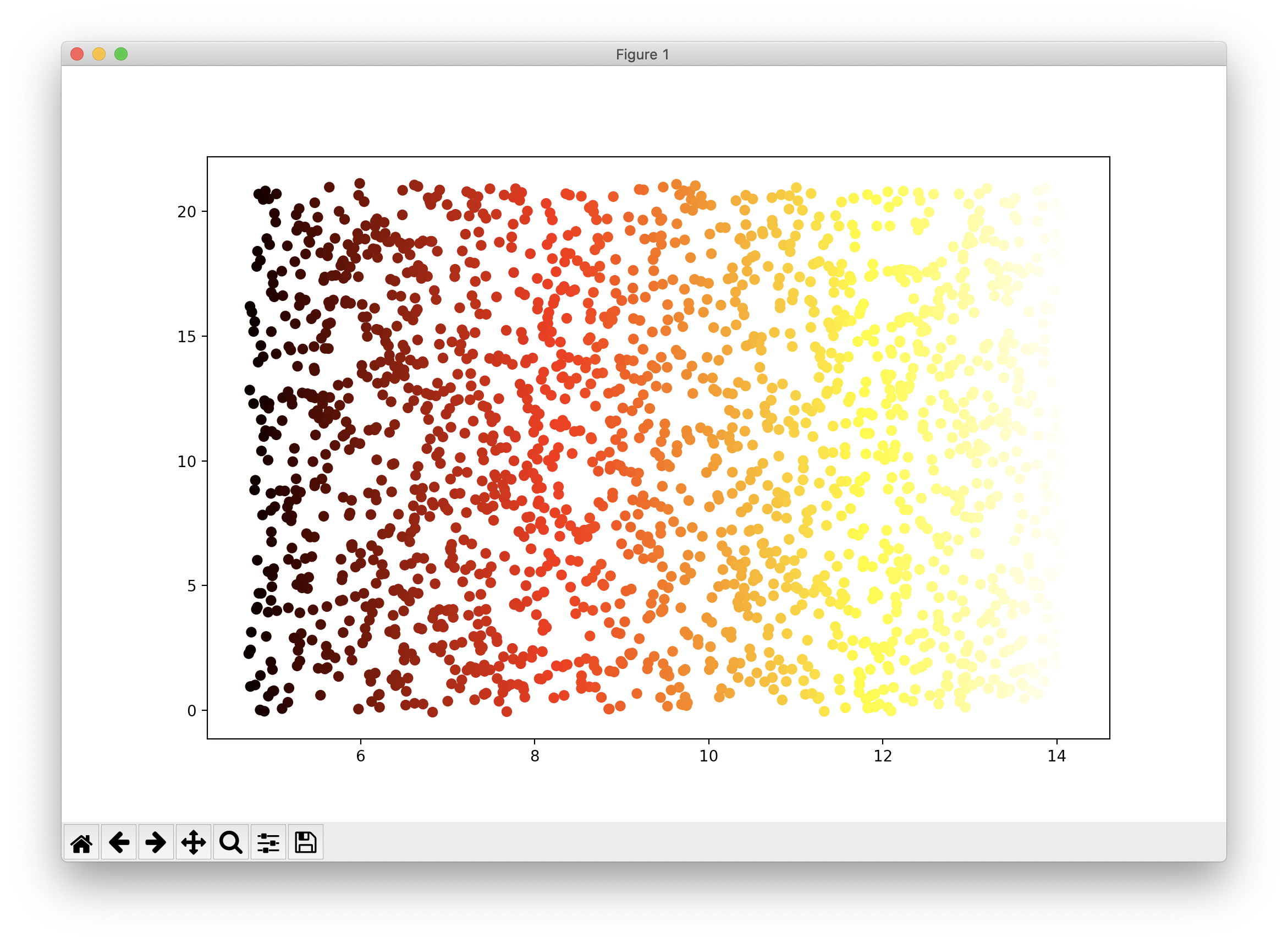
스위스롤 데이터셋에 대한 차원축소에 대한 최고의 결과는 바로 위의 결과라고도 할 수 있습니다. 하지만 이러한 해석은 2차원상의 시각화라는 관점에서만 국한된 결과입니다.
이제 실제 차원축소에 대한 다양한 방법을 코드로 살펴보겠습니다. 먼저 PCA입니다.
from sklearn.decomposition import PCA X_pca_reduced = PCA(n_components=2, random_state=42).fit_transform(X) plt.scatter(X_pca_reduced[:, 0], X_pca_reduced[:, 1], c=t, cmap=plt.cm.hot) plt.show()
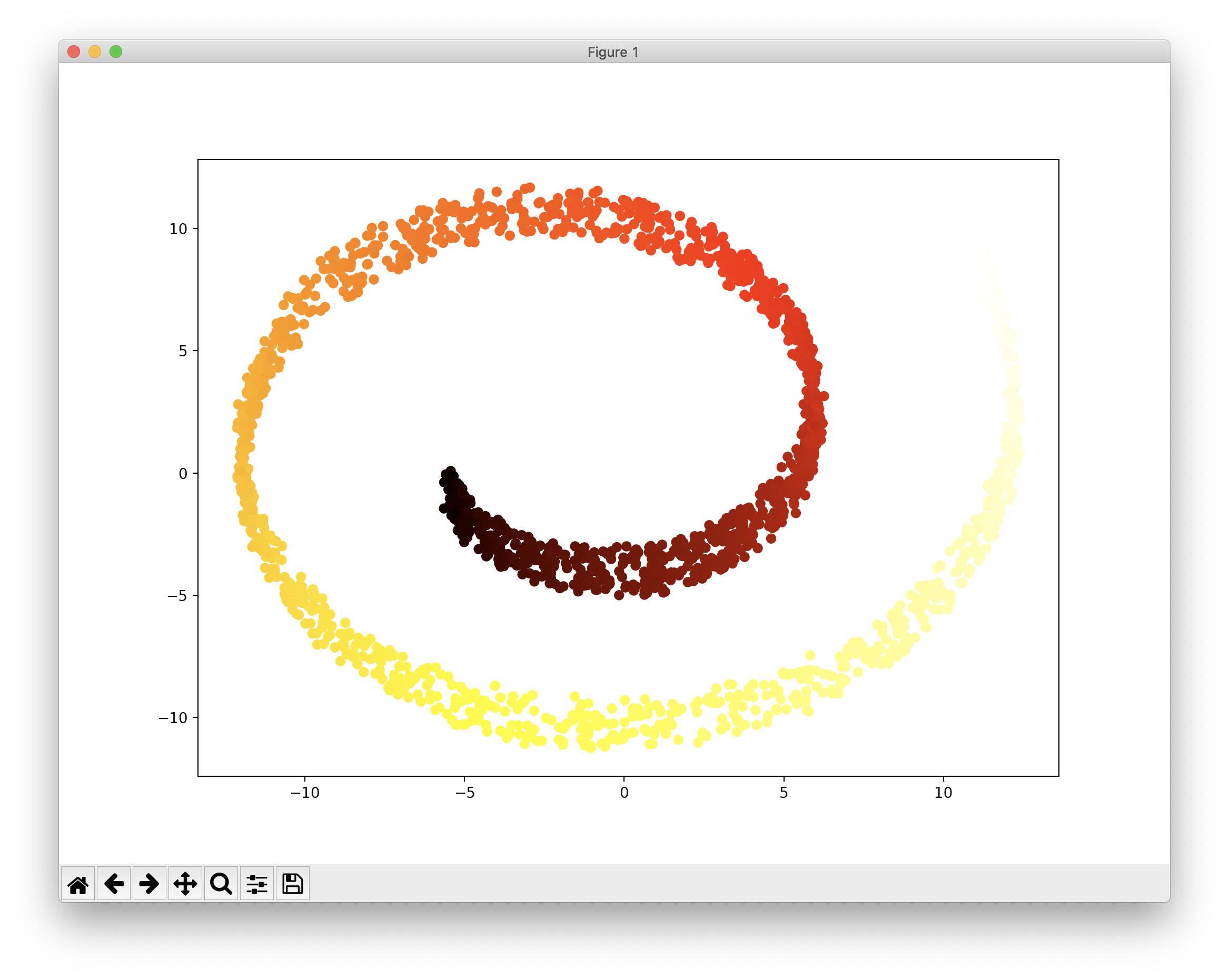
다음은 PCA의 비선형 버전인 Kernel PCA입니다.
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components=2, kernel="linear")
rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.05)
sig_pca = KernelPCA(n_components=2, kernel="sigmoid", gamma=0.001, coef0=1)
plt.figure(figsize=(11, 4))
for subplot, pca, title in (
(131, lin_pca, "Linear kernel"),
(132, rbf_pca, "RBF kernel, $\gamma=0.05$"),
(133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.show()
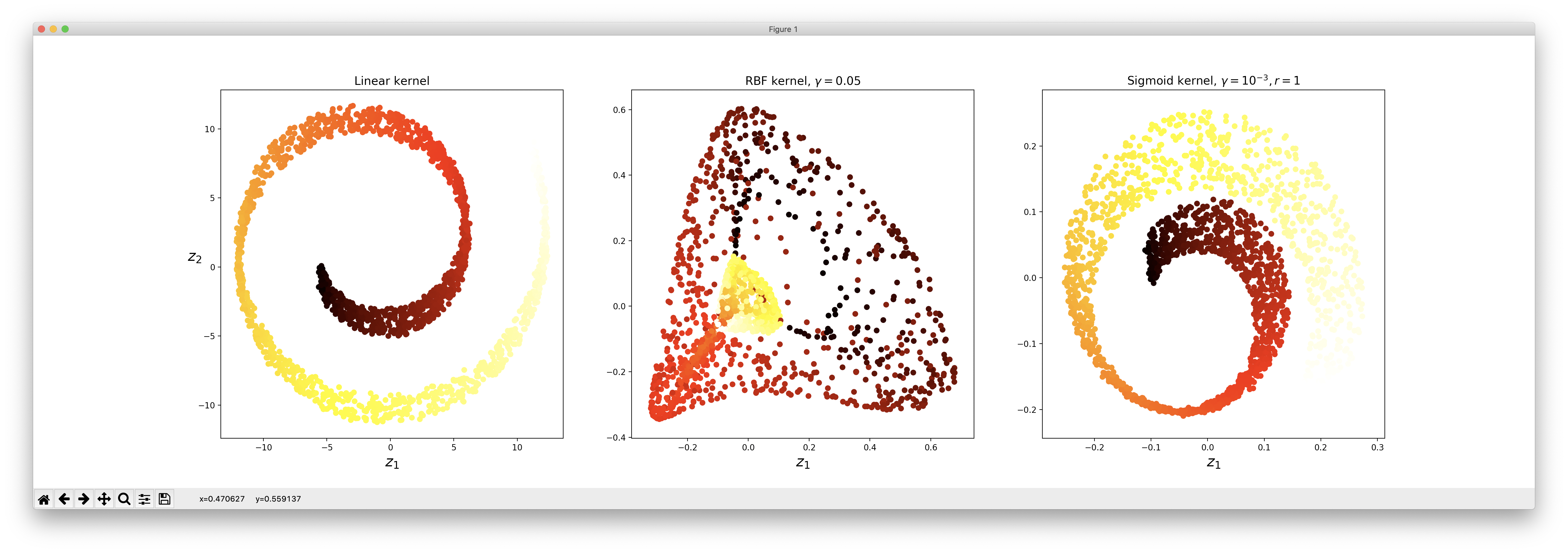
위의 코드는 3가지 종류의 커널에 대한 PCA 결과를 표현하고 있습니다.
다음은 LLE 알고리즘을 사용한 차원축소입니다. LLE는 Locally Linear Embedding으로 국소적인(지역적인) 샘플 데이터간 거리를 최대한 보존하며 차원을 축소합니다. 코드 및 그 결과는 아래와 같습니다.
from sklearn.manifold import LocallyLinearEmbedding lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=3224) X_reduced = lle.fit_transform(X) plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot) plt.show()
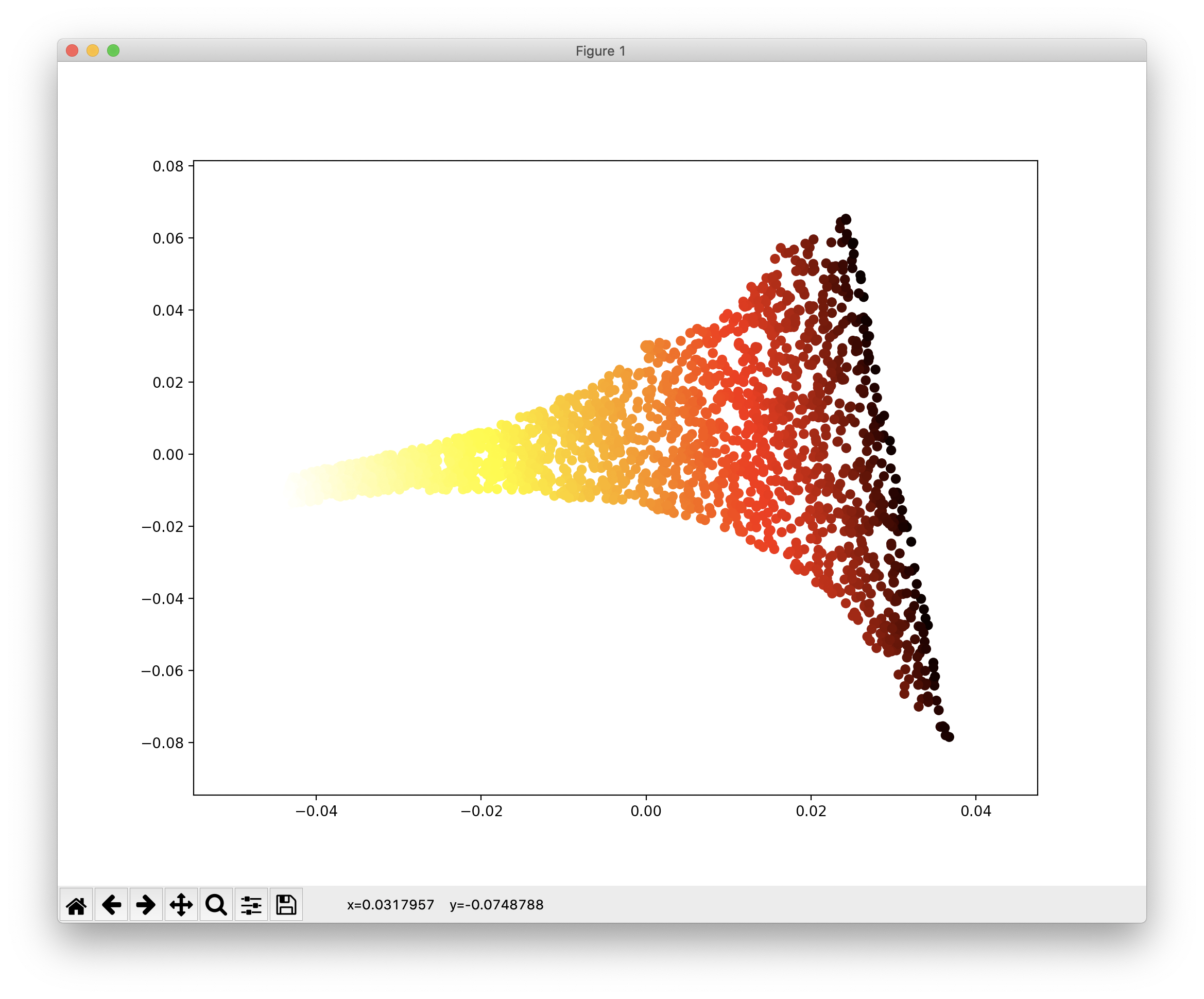
다음은 MDS로 다차원 스케일링(Multi-Dimensional Scaling)의 약자로, 샘플 데이터 간의 거리르 보존하면서 차원을 축소합니다. 코드 예와 그 결과는 다음과 같습니다.
from sklearn.manifold import MDS mds = MDS(n_components=2, random_state=3224) X_reduced_mds = mds.fit_transform(X) plt.scatter(X_reduced_mds[:, 0], X_reduced_mds[:, 1], c=t, cmap=plt.cm.hot) plt.show()
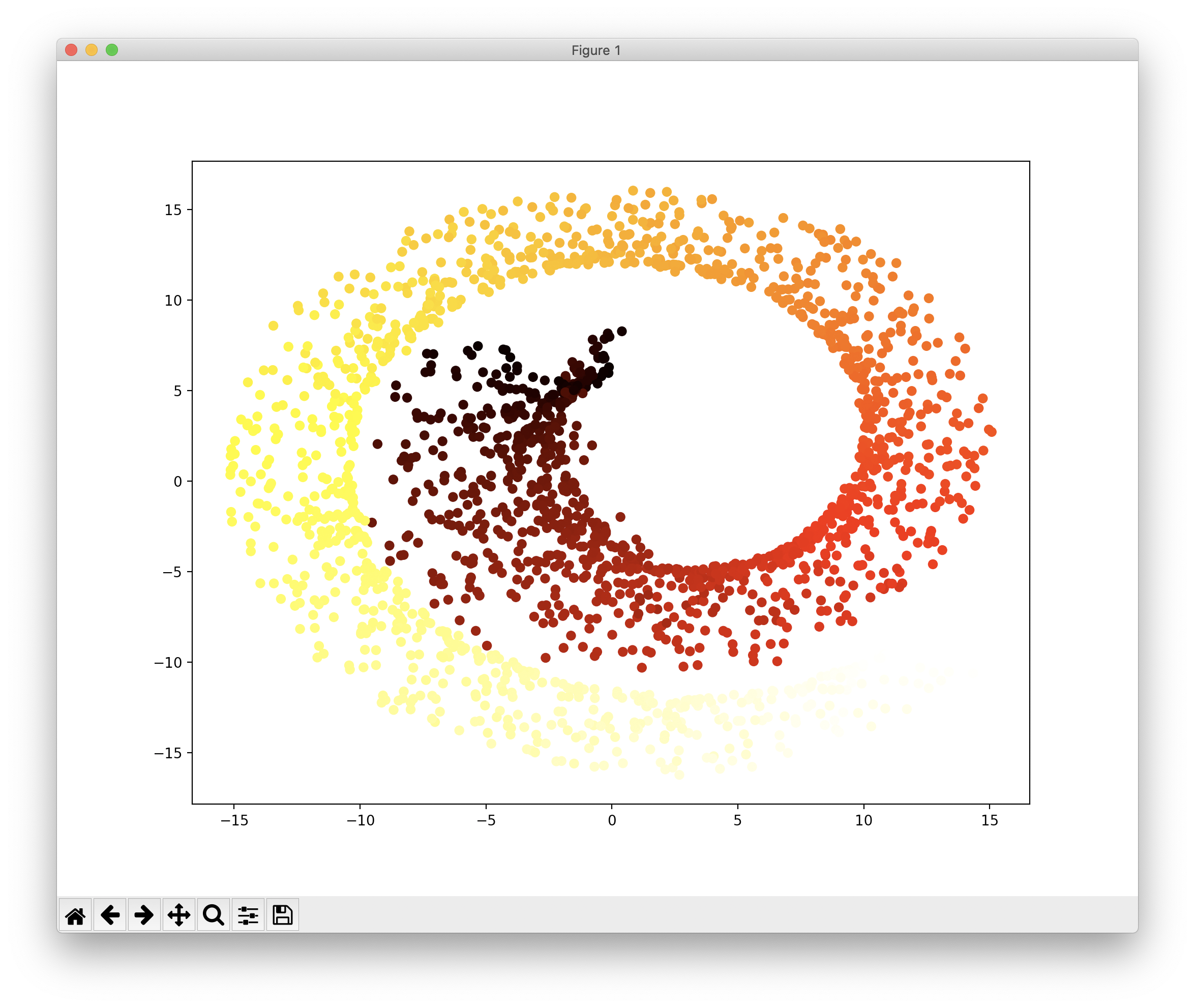
다음은 Isomap을 이용한 차원축소이며, 이는 각 샘플에서 가장 가까운 샘플 간의 거리, 보다 정확히는 Geodesic Distance를 유지하면서 차원을 축소합니다. 코드와 그 결과는 다음과 같습니다.
from sklearn.manifold import Isomap isomap = Isomap(n_components=2) X_reduced_isomap = isomap.fit_transform(X) plt.scatter(X_reduced_isomap[:, 0], X_reduced_isomap[:, 1], c=t, cmap=plt.cm.hot) plt.show()
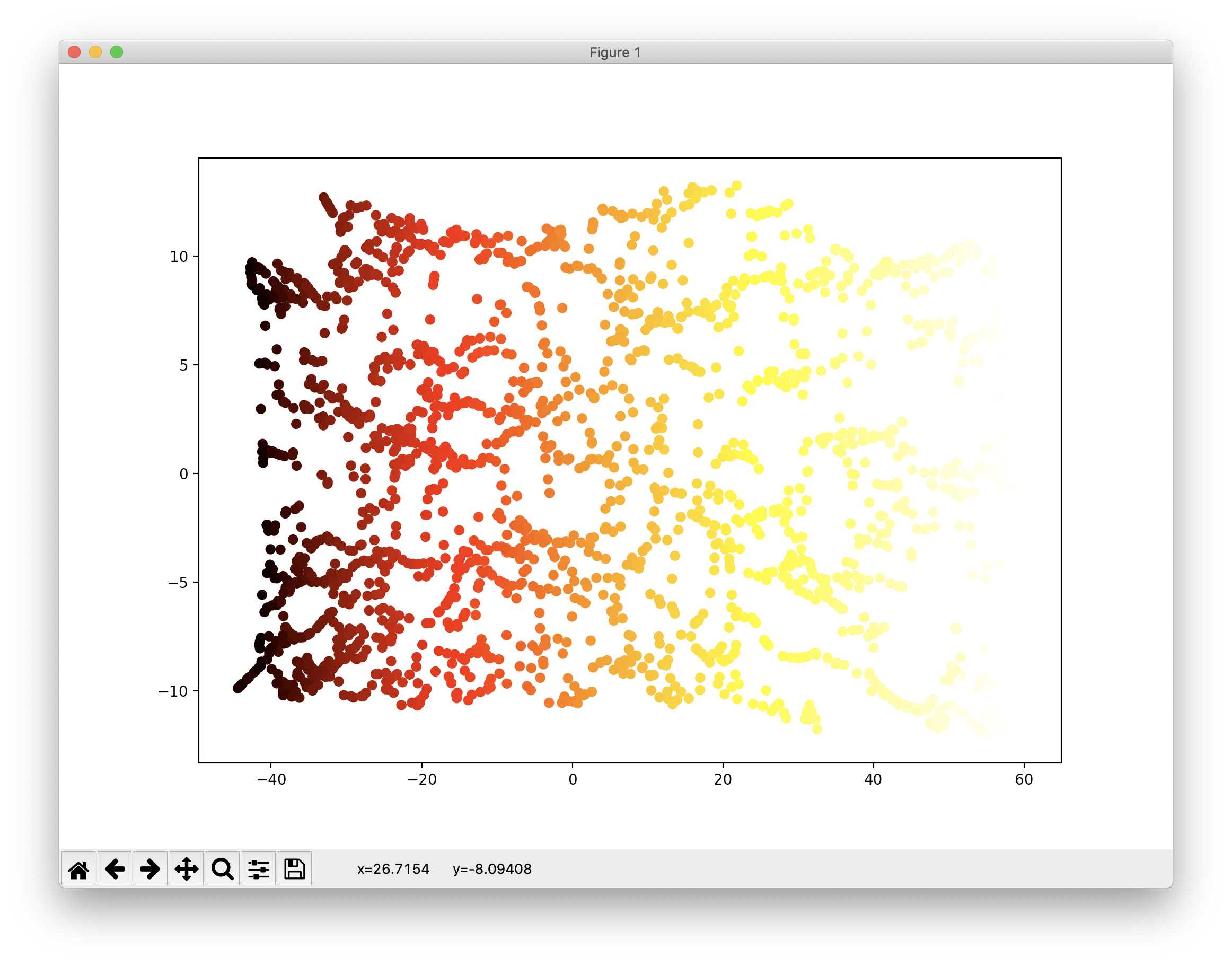
더 많은 차원축소 방법이 존재하지만 이 글에서는 마지막으로 t-SNE을 이용한 차원감소를 소개합니다. 주로 시각화에 많이 사용되며 군집화된 결과를 시각적으로 표현합니다. 코드와 결과는 다음과 같습니다.
from sklearn.manifold import TSNE tsne = TSNE(n_components=2, random_state=3224) X_reduced_tsne = tsne.fit_transform(X) plt.scatter(X_reduced_tsne[:, 0], X_reduced_tsne[:, 1], c=t, cmap=plt.cm.hot) plt.show()
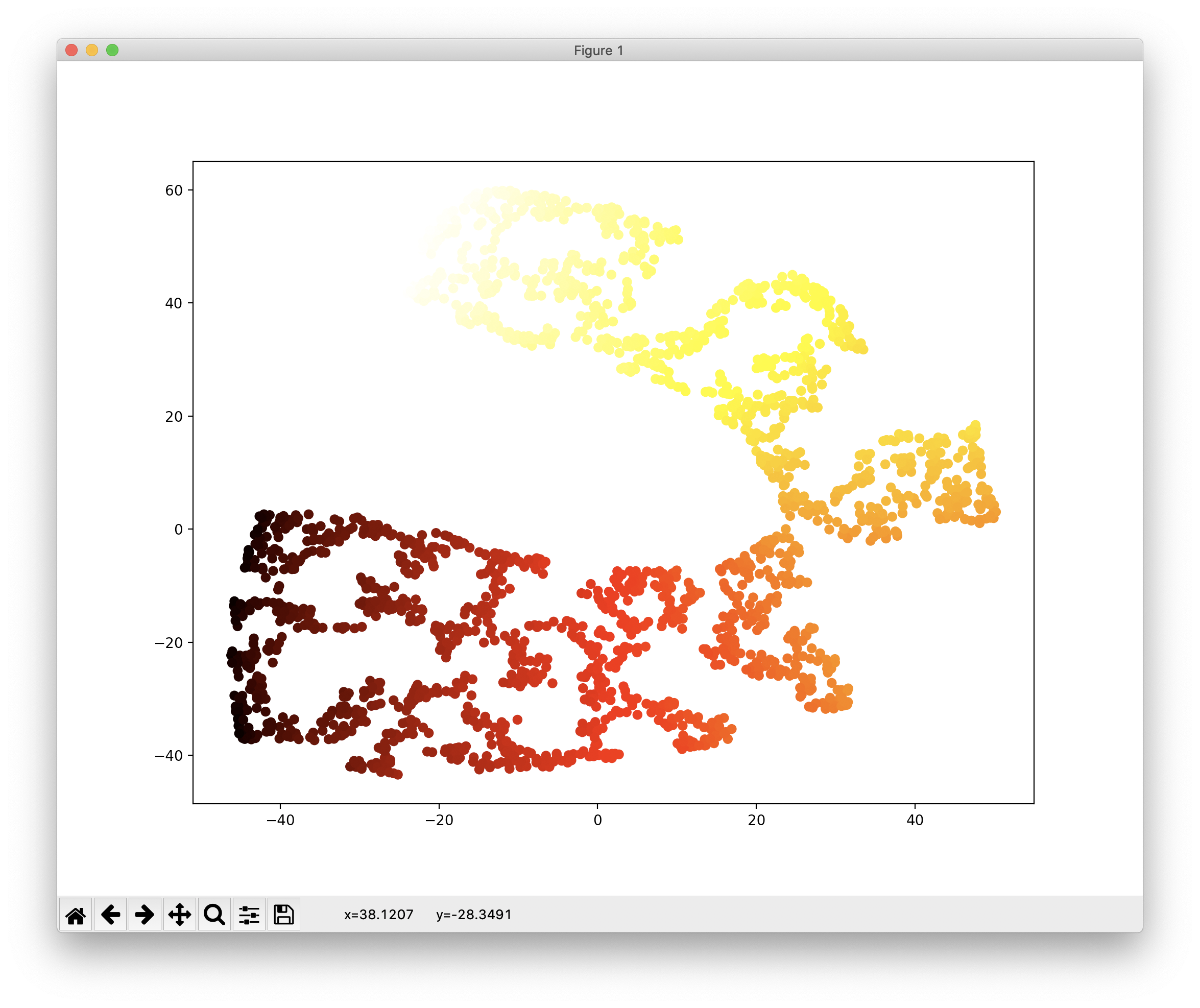
t-SNE를 이용한 다른 글은 아래의 링크를 참조하시기 바랍니다.
단순 선형 회귀에 대한 2가지 접근
잡음이 섞인 샘플 데이터가 선형이라고 가정할때, 이 선형 모델은 기울기와 절편이라는 값으로 정의됩니다. 이 기울기와 절펀에 대한 값을 구하는 방법은 다양한데, 이 글에서는 2가지 접근 방법을 언급합니다. 먼저 잡음이 섞인 샘플 데이터는 다음과 같습니다.
import numpy as np import matplotlib.pyplot as plt X = 10 * np.random.rand(100,1) y = 3.7 - 2.5 * X + np.random.randn(100,1) plt.scatter(X, y) plt.show()
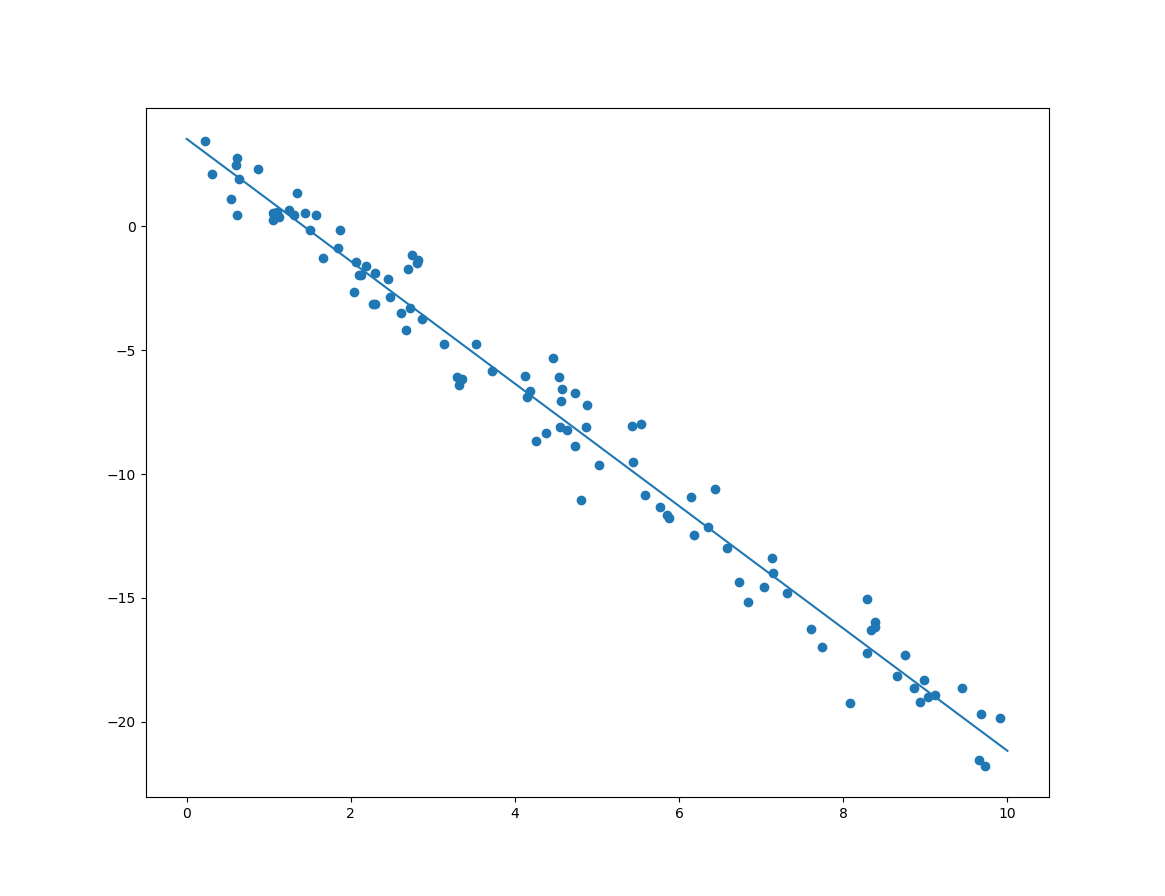
위의 코드는 샘플 데이터에 대한 시각화 코드도 포함하고 있는데, 그 결과는 다음과 같습니다.
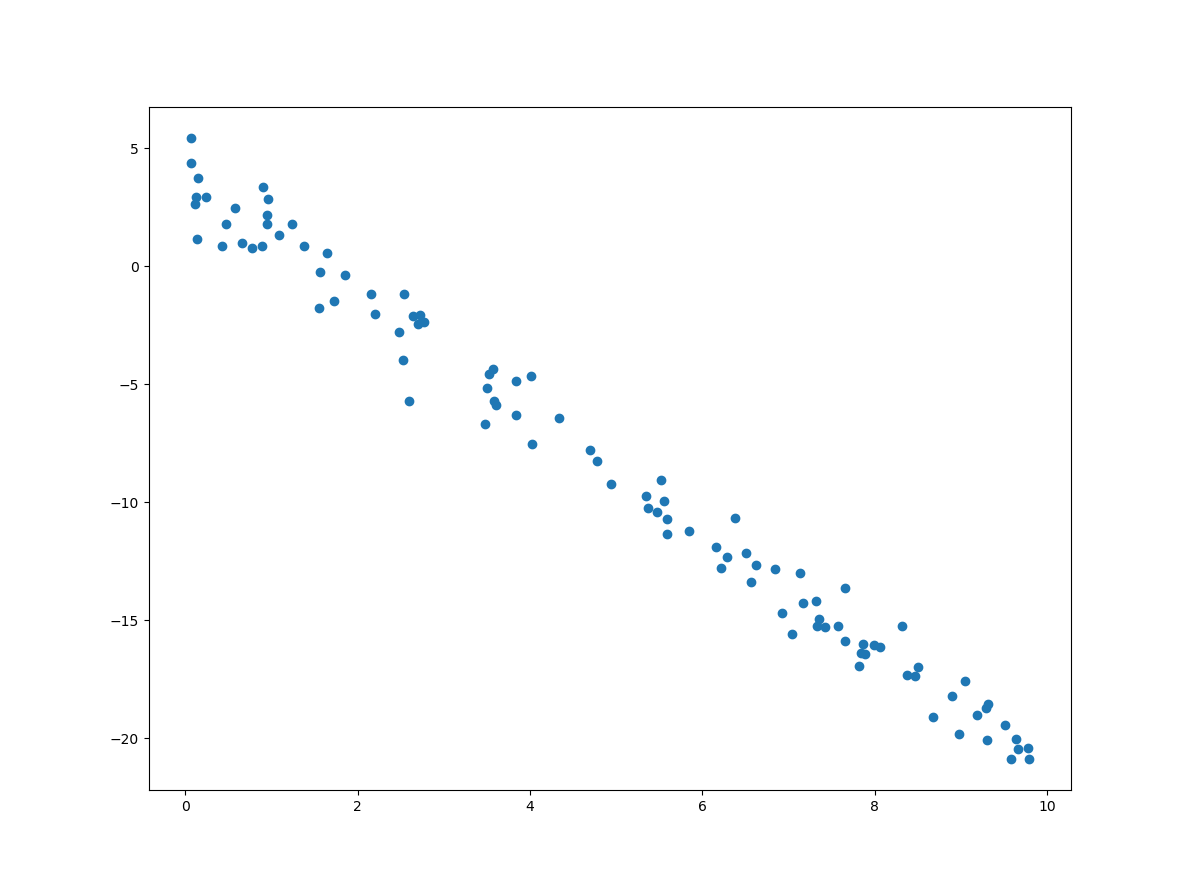
이제 위의 샘플 데이터에 대한 선형회귀 방법 중 하나인 정규방정식(Normal Equation)에 대한 코드는 다음과 같습니다.
X_b = np.c_[np.ones((100,1)), X] w = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) print(w) plt.scatter(X, y) drawLine(w[1], w[0]) plt.show()
분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.
[[ 3.76686801] [-2.50677558]]
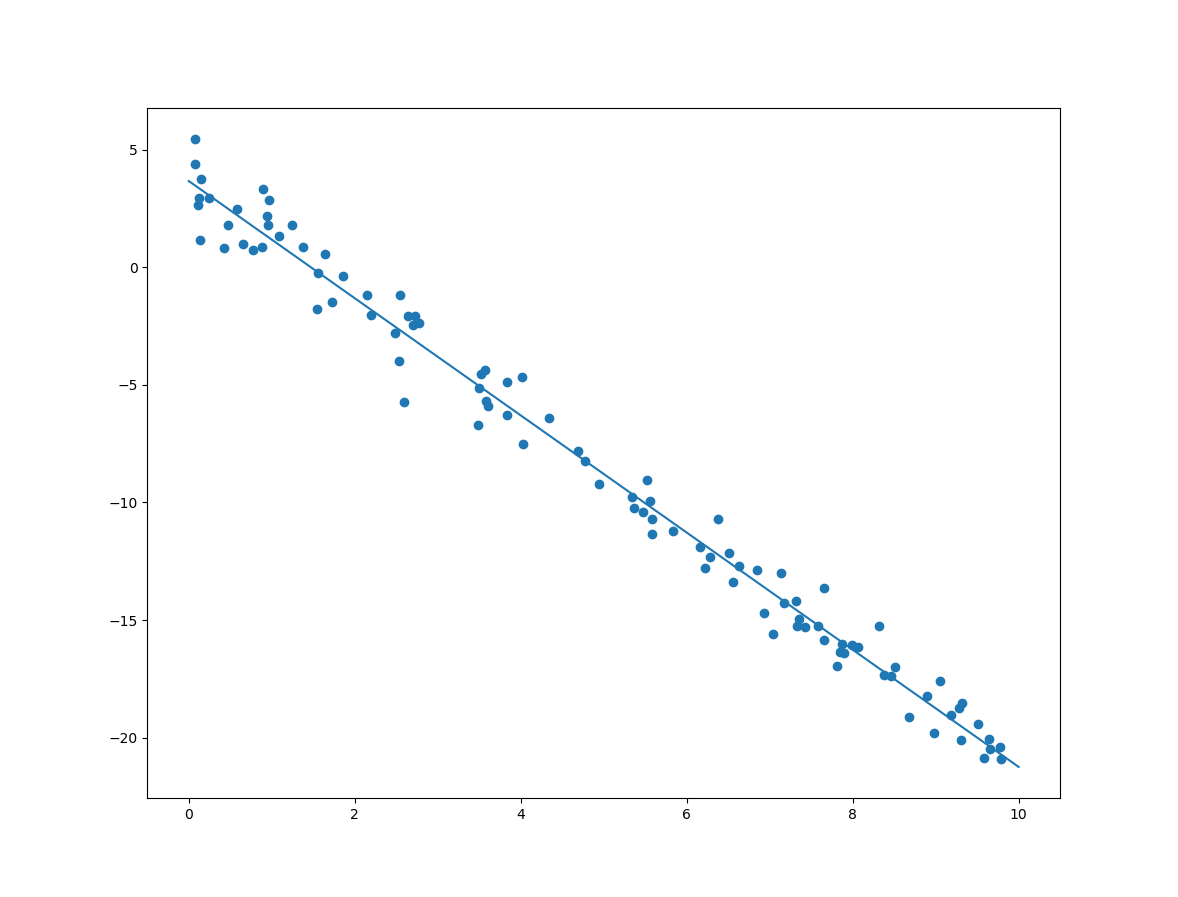
아울러 정규방정식은 다음과 같습니다.
![]()
다음은 사이킷런에서 제공하는 LinearRegression 클래스를 이용한 방법입니다.
from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X, y) w = [model.intercept_[0], model.coef_[0][0]] print(w) plt.scatter(X, y) drawLine(w[1], w[0]) plt.show()
분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.
[[ 3.69686801] [-2.50677558]]
위의 코드에서 절편과 기울기를 통해 그래프를 그리는 함수인 drawLine은 다음과 같습니다.
def drawLine(m, b):
X = np.arange(0, 11)
y = [m * x + b for x in X]
plt.plot(X, y)
혼돈행렬(Confusion Matrix)와 정밀도, 재현률, F1점수
이 글은 한빛미디어의 핸즈온 머신러닝을 수업자료로써 파악하면서 이해한 바를 짧게 요약한 글입니다. 요즘 이 책을 통해 머신러닝을 다시 접하고 있는데, 체계적이고 좋은 내용을 제공하고 있고, 나 자신을 위한 보다 명확한 이해를 돕고자 이 글을 작성 작성합니다. 요즘 제가 블로그에 올리는 머신러닝 관련 글은 대부분 이 책의 내용에 대한 나름대로의 해석을 토대로 합니다. 보다 자세한 내용은 해당 도서를 참고하기 바랍니다.
이글은 훈련된 예측 모델을 평가하기 위한 지표인 정밀도, 재현률, F1에 대한 내용입니다. 이러한 평가 지표는 혼돈행렬이라는 데이터를 토대로 계산되는데요, 먼저 혼돈행렬을 구하기 위해 학습 데이터셋이 필요하며, 0~9까지의 숫자를 손으로 작성한 MINIST를 사용하고, 이 손글씨가 7인지에 대한 예측 모델을 예로 합니다. MNIST 데이터셋을 다운로드 받고, 레이블 데이터를 재가공합니다.
from sklearn.datasets import fetch_openml
import numpy as np
mnist = fetch_openml('mnist_784', version=1, data_home='D:/__Temp__/_')
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_7 = (y_train == 7)
y_test_7 = (y_test == 7)
예측 모델은 SGDClassifier를 사용합니다.
from sklearn.linear_model import SGDClassifier model = SGDClassifier(random_state=3224)
혼돈 행렬을 얻기 위해 다음 코드를 실행합니다.
from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix y_train_pred = cross_val_predict(model, X_train, y_train_7, cv=3) cf = confusion_matrix(y_train_7, y_train_pred) print(cf)
[[53223 512] [ 726 5539]]
cross_val_predict 함수는 아직 전혀 학습이 되지 않은 모델을 지정된 교차검증 수만큼 학습시킨 뒤 예측값을 반환합니다. 이렇게 얻은 예측값과 실제 값을 비교해서 얻은 혼돈행렬의 결과에 대한 상세한 이미지는 아래와 같습니다.
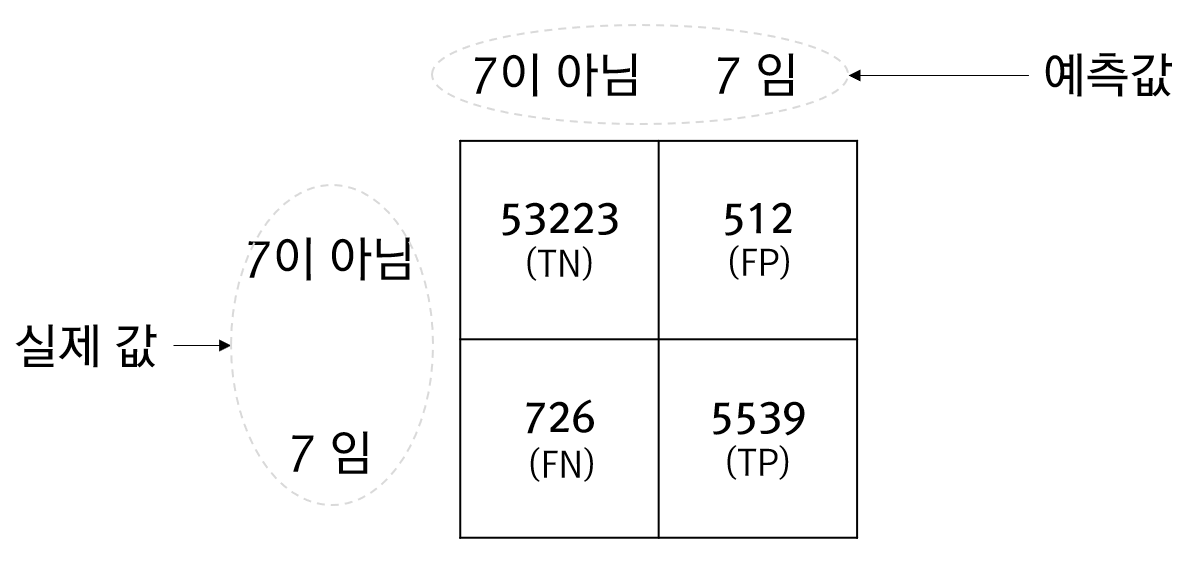
위의 그림에서 표에 담긴 4개의 값은 발생횟수입니다. TN과 TP의 값은 옳바르게 예측한 횟수이고 FN과 FP는 잘못 예측한 횟수입니다. 즉, FN과 FP가 0일때 모델은 완벽하다는 의미입니다.
이제 위의 혼돈행렬에서 정밀도(Precision)와 재현률(Recall), F1점수에 대한 수식은 다음과 같습니다.
![]()
정밀도와 재현률이 서로 상반관계에 있습니다. 즉, 정밀도가 높으면 재현률이 떨어지며 재현률이 높아지면 정밀도가 떨어지는 경향이 있습니다. F1은 이런 상반관계에 있는 정밀도와 재현률을 묶어 평가하고자 하는 지표입니다.
비록 정밀도와 재현률, F1점수는 매우 단순해 계산하기 쉬우나 다음의 코드를 통해서도 쉽게 얻을 수 있습니다.
from sklearn.metrics import precision_score, recall_score, f1_score p = precision_score(y_train_7, y_train_pred) print(p) r = recall_score(y_train_7, y_train_pred) print(r) f1 = f1_score(y_train_7, y_train_pred) print(f1)
0.9153858866303091 0.8841181165203511 0.8994803507632347
