이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_geometric_transformations/py_geometric_transformations.html#geometric-transformations 입니다.
OpenCV는 cv2.wrapAffine, cv2.warpPerspective라는 2개의 변환 함수를 제공하는데 각각 2×3 행렬과 3×3 행렬을 인자로 받습니다. 이 함수를 통해 이미지에 대한 크기 변환, 이동, 회전, Affine 변환, Perspective 변환을 수행할 수 있습니다.
먼저 이미지 크기 변환인데, 이 경우 위의 함수를 통한 변환도 가능하지만 OpenCV에서는 cv2.resize 함수를 이용해 크기 변환을 자주 수행하며 예제는 아래와 같습니다.
import cv2
import numpy as np
img = cv2.imread('./data/Penguins.jpg', 0)
res1 = cv2.resize(img,None,fx=2, fy=2, interpolation = cv2.INTER_CUBIC)
height, width = img.shape[:2]
res2 = cv2.resize(img,(2*width, 2*height), interpolation = cv2.INTER_CUBIC)
cv2.imshow('res1', res1)
cv2.imshow('res2', res2)
cv2.waitKey()
cv2.destroyAllWindows()
6번과 9번 코드 모두 이미지를 2배 확대하는데, 9번 코드의 경우 이미지의 픽셀 크기로 확대정도를 지정하므로 소수점으로 확대, 축소는 할 수 없습니다.
다음은 이미지를 이동하는 변환입니다. 이동 변환을 위한 행렬은 다음과 같습니다.
![]()
위의 행렬을 적용하는 코드는 다음과 같은데, 이미지를 x축으로 100만큼, y축으로 50만큼 이동합니다. 이동되고 남은 공간은 0값으로 채워지므로 검정색으로 표시됩니다.
import cv2
import numpy as np
img = cv2.imread('./data/Penguins.jpg', 0)
M = np.float32(
[
[1, 0,100],
[0, 1, 50]
]
)
rows,cols = img.shape
dst = cv2.warpAffine(img, M, (cols,rows))
cv2.imshow('img',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
다음은 회전입니다. 2차원에 대한 일반적인 회전 행렬은 다음과 같습니다.
![]()
이를 2×3인 행렬로 표현해야 Affine 변환이 가능한데, 이를 위해 OpenCV는 cv2.getRotationMatrix2D 라는 함수를 통해 회전 행렬을 얻을 수 있습니다. 이 함수는 장점은 회전값의 지정뿐만 아니라 크기 변환과 회전중심점도 지정할 수 있습니다. 이 함수를 통해 얻을 수 있는 행렬은 다음과 같습니다.
![]()
위의 기호에 대해서
![]()
예제는 다음과 같습니다.
import cv2
import numpy as np
img = cv2.imread('./data/Penguins.jpg', 0)
rows,cols = img.shape
M = cv2.getRotationMatrix2D((cols/2,rows/2), 45, 0.6)
print(M)
dst = cv2.warpAffine(img,M,(cols,rows))
cv2.imshow('img',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
8번 코드를 보면 회전 중심을 이미지의 중심 좌표로 했고, 회전각도는 45도, 크기변환 비율은 0.6으로 지정하여 원래 크기의 60%로 변환됩니다. 결과는 다음과 같습니다.

Affine 변환에 대해 살펴보겠습니다. Affine 변환은 크기변환, 이동변환, 회전변환이 발생해도 원래 평행했던 특성이 그대로 유지됩니다. 이러한 특성을 갖는 Affine 변환에 대한 행렬은 cv2.getAffineTransform을 통해 얻을 수 있으며 그 결과는 2×3 행렬입니다. 아래는 예제입니다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('./data/chessboard2.jpg')
rows,cols,ch = img.shape
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv2.getAffineTransform(pts1,pts2)
dst = cv2.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
결과는 다음과 같은데..
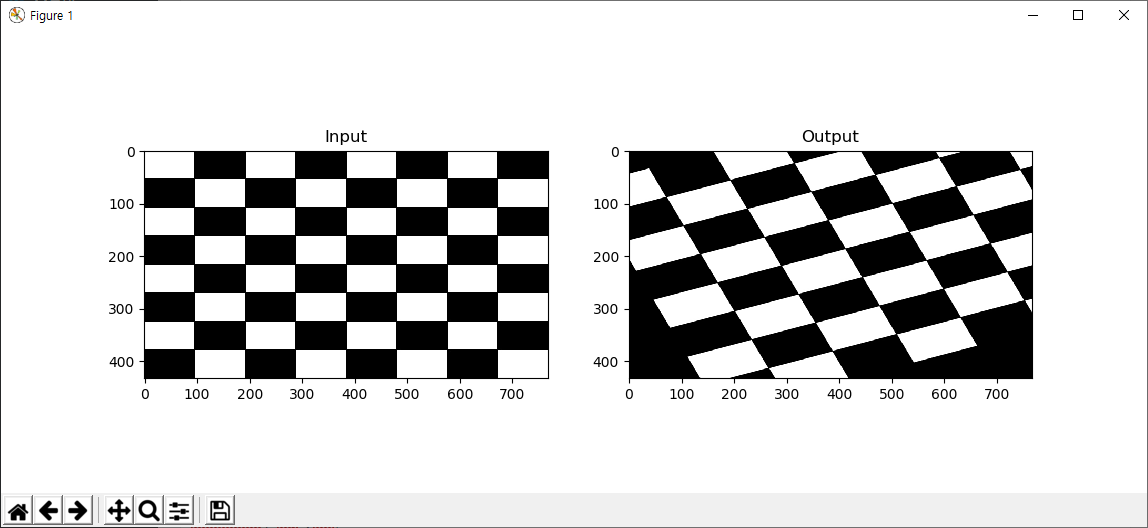
위 코드에서 8번의 3개의 좌표가 9번의 3개의 각각의 좌표로 변환됨에 있어서 평행을 유지하도록 하는 행렬을 얻는다는 것입니다.
다음은 Perspective 변환, 즉 투영변환입니다. 이 변환은 지금까지의 2×3 행렬이 아닌 3×3 행렬입니다. 변환 후에 평행성은 더 이상 유효하지 않습니다. 예제는 다음과 같습니다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('./data/chessboard2.jpg')
rows,cols,ch = img.shape
pts1 = np.float32([[0,0],[368,52],[28,387],[389,390]])
pts2 = np.float32([[32,32],[300,0],[0,300],[300,300]])
M = cv2.getPerspectiveTransform(pts1,pts2)
dst = cv2.warpPerspective(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
결과는 다음과 같습니다.
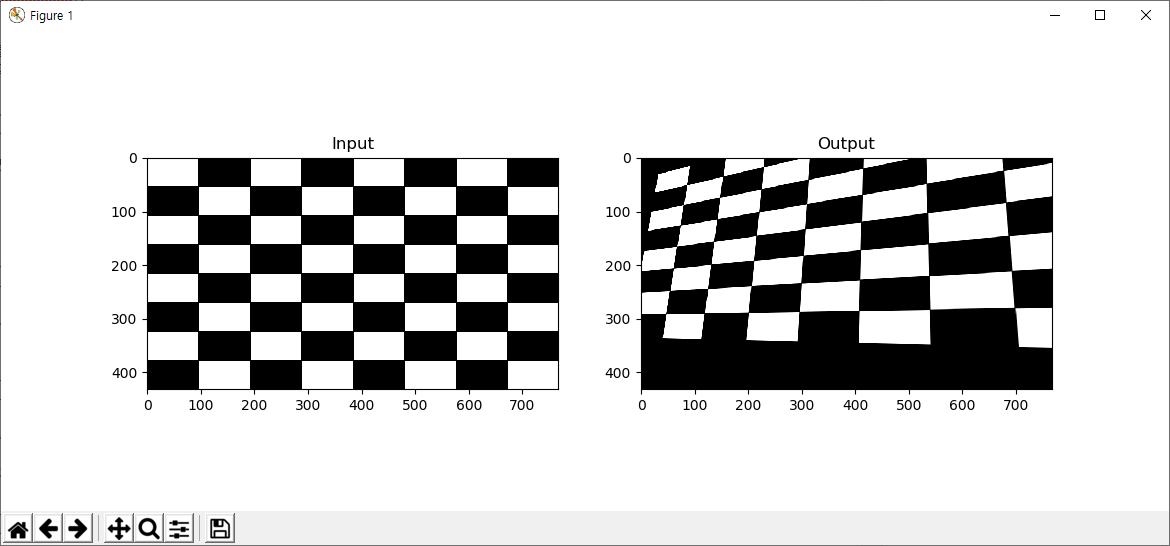
9번에서 지정한 4개의 좌표가 10번에서 지정한 4개의 좌표로, 각각 매칭되어 변환이 이루어지는 행렬을 얻는 것이고 이렇게 얻은 행렬은 14번 코드의 cv2.warpPerspective 함수에 의해 변환이 수행됩니다.