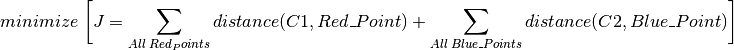이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_ml/py_svm/py_svm_opencv/py_svm_opencv.html 입니다.
이 글은 kNN 대신 SVM를 사용한 OCR 기능을 OpenCV로 구현하는 예제에 대한 설명입니다.
kNN에서는 특징 벡터(Feature Vector)로써 픽셀의 밝기(Intensity)를 사용했습니다. 이번에는 특징 벡터로써 HOF(Histogram of Oriented Gradients)를 사용하도록 하겠습니다.
HOG를 찾기 전에, 먼저 이미지의 Moments(정확히는 Second Order Moments)를 사용해 기울어진 이미지를 보정합니다. 먼저 deskew() 함수를 정의할텐데, 이 함수는 숫자 이미지를 읽어 기울어진 모양을 바로 잡습니다. 아래는 deskew() 함수입니다.
SZ=20
affine_flags = cv2.WARP_INVERSE_MAP|cv2.INTER_LINEAR
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11']/m['mu02']
M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
img = cv2.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
return img
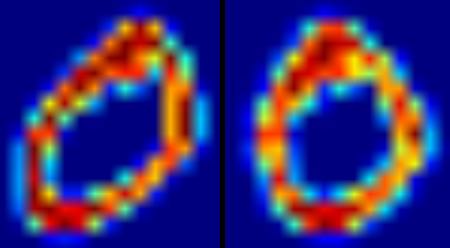
아래의 이미지는 숫자 0에 대한 입력 이미지(왼쪽)를 deskew 함수에 적용한 결과(오른쪽)입니다.
다음은 각 셀의 HOG 디스크립터를 찾는 것입니다. 이를 위해, X축과 Y축 방향으로 각 셀의 Sobel 결과를 얻습니다. 그리고는 이 결과에 대한 각 픽셀에서 그레디언트(Gradient)의 크기와 방향을 얻습니다. 이 그레디언트는 16개의 정수값으로 변환합니다. 이 이미지를 4개의 부분 사각형으로 분할합니다. 각각의 부분 사각형에 대해, 이들의 크기값을 가지는 가중치 방향(16 Bins)의 히스토그램을 계산합니다. 그러면 각각의 부분 사각형을 통해 16개의 값을 가진 벡터가 생성됩니다. 4개의 각 벡터(4개의 부분 사각형)를 합치면 64개의 값을 갖는 특징 벡터를 얻게 됩니다. 이 특징 벡터를 훈련 데이터로 사용합니다. 아래의 코드는 지금까지의 설명에 대한 코드입니다.
bin_n = 16 # Number of bins
def hog(img):
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1)
mag, ang = cv2.cartToPolar(gx, gy)
bins = np.int32(bin_n*ang/(2*np.pi)) # quantizing binvalues in (0...16)
bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
hist = np.hstack(hists) # hist is a 64 bit vector
return hist
마지막으로, 이전 경우에서처럼, 숫자가 쓰여진 큰 이미지를 각 셀로 조각냅니다. 각 문자에 대해, 250개의 셀은 훈련 데이터로.. 나머지는 시험 테이터로 사용할 것입니다. 아래는 이에 대한 설명과 앞서 언급한 2개의 함수 모두를 합한 전체 코드입니다.
import cv2
import numpy as np
SZ=20
affine_flags = cv2.WARP_INVERSE_MAP|cv2.INTER_LINEAR
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11']/m['mu02']
M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
img = cv2.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
return img
bin_n = 16 # Number of bins
def hog(img):
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1)
mag, ang = cv2.cartToPolar(gx, gy)
bins = np.int32(bin_n*ang/(2*np.pi)) # quantizing binvalues in (0...16)
bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
hist = np.hstack(hists) # hist is a 64 bit vector
return hist
img = cv2.imread('./data/digits.png',0)
cells = [np.hsplit(row,100) for row in np.vsplit(img,50)]
# First half is trainData, remaining is testData
train_cells = [ i[:50] for i in cells ]
test_cells = [ i[50:] for i in cells]
###### Now training ########################
deskewed = [list(map(deskew,row)) for row in train_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
trainData = np.float32(hogdata).reshape(-1,64)
responses = np.repeat(np.arange(10),250)[:,np.newaxis]
svm = cv2.ml.SVM_create()
svm.setKernel(cv2.ml.SVM_LINEAR)
svm.setType(cv2.ml.SVM_C_SVC)
svm.setC(2.67)
svm.setGamma(5.383)
svm.train(trainData, cv2.ml.ROW_SAMPLE, responses)
svm.save('svm_data.dat')
###### Now testing ########################
deskewed = [list(map(deskew,row)) for row in test_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
testData = np.float32(hogdata).reshape(-1,bin_n*4)
result = svm.predict(testData)[1]
####### Check Accuracy ########################
mask = result==responses
correct = np.count_nonzero(mask)
print(correct*100.0/result.size)
결과는 93.8로써 인식 성공률입니다. kNN에서의 인식률은 91.76였는데.. 그보다 더 나은 인식률을 보이고 있습니다.
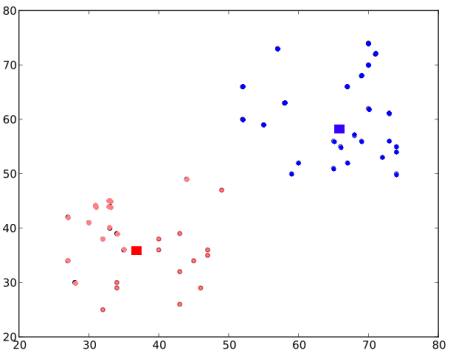
![]() 와
와 ![]() 사이의 거리합이 최소입니다.
사이의 거리합이 최소입니다.