[카테고리:] Python

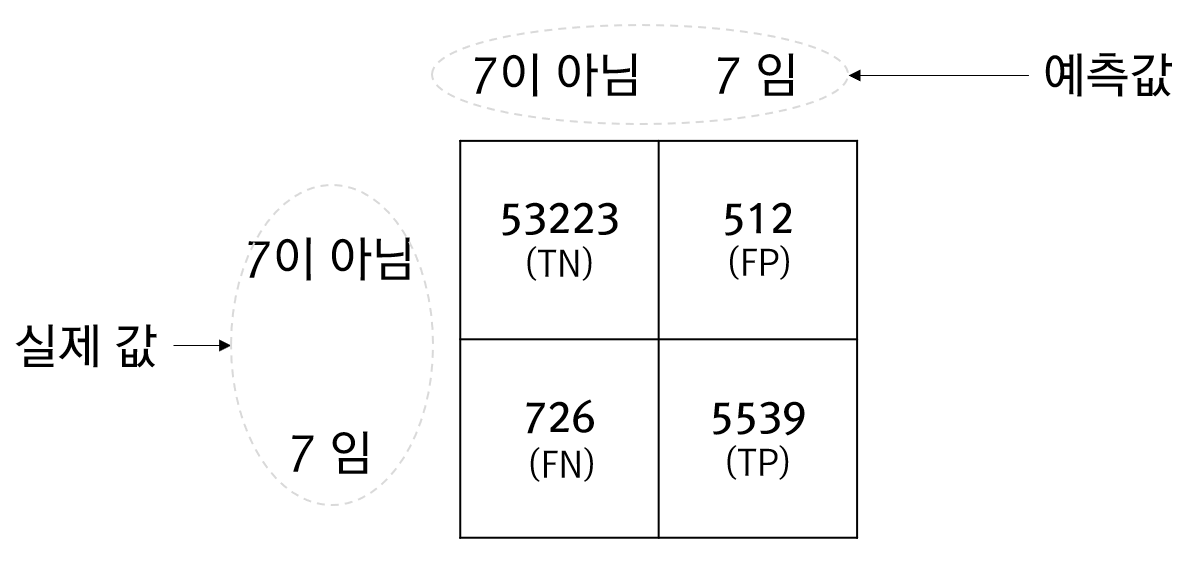
잡음이 섞인 샘플 데이터가 선형이라고 가정할때, 이 선형 모델은 기울기와 절편이라는 값으로 정의됩니다. 이 기울기와 절펀에 대한 값을 구하는 방법은 다양한데, 이 글에서는 2가지 접근 방법을 언급합니다. 먼저 잡음이 섞인 샘플 데이터는 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt

X = 10 * np.random.rand(100,1)
y = 3.7 - 2.5 * X + np.random.randn(100,1)
plt.scatter(X, y)
plt.show()

위의 코드는 샘플 데이터에 대한 시각화 코드도 포함하고 있는데, 그 결과는 다음과 같습니다.

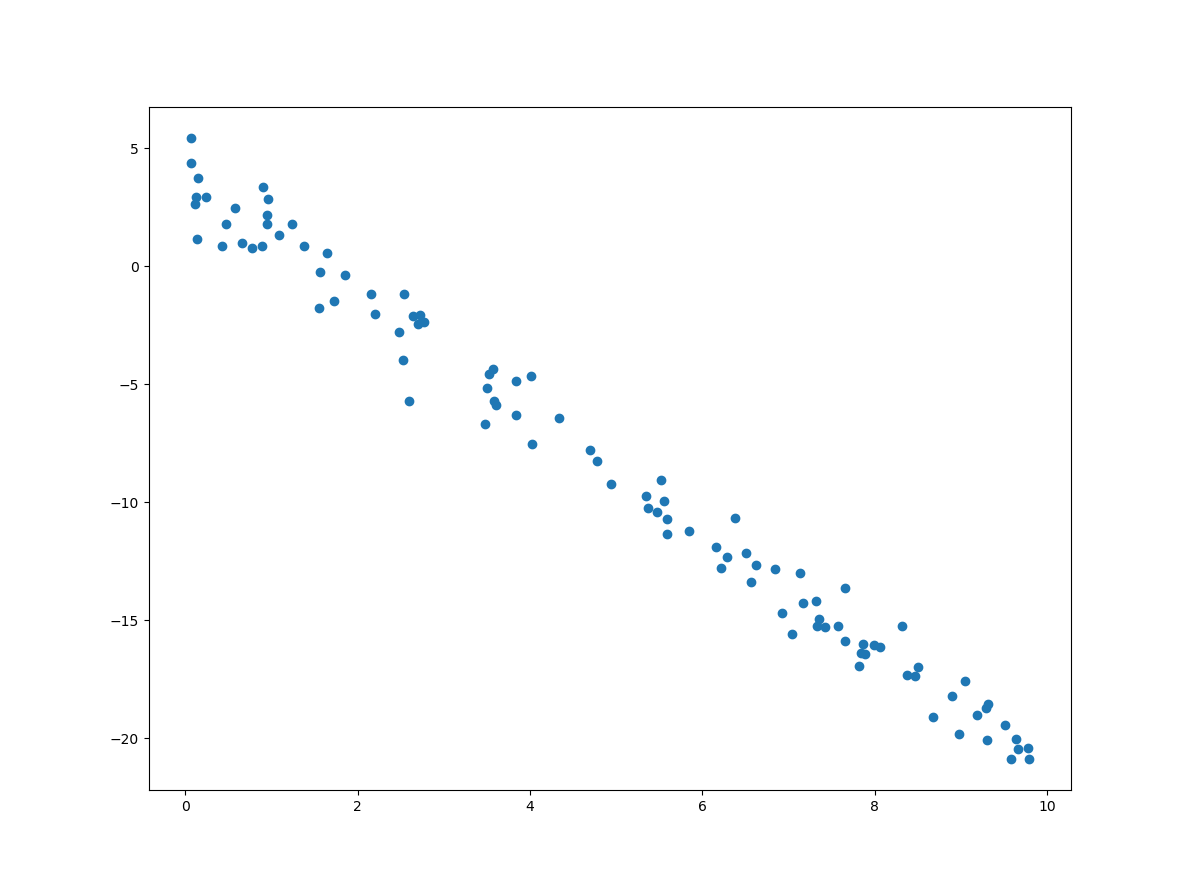
이제 위의 샘플 데이터에 대한 선형회귀 방법 중 하나인 정규방정식(Normal Equation)에 대한 코드는 다음과 같습니다.

X_b = np.c_[np.ones((100,1)), X]
w = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(w)

plt.scatter(X, y)
drawLine(w[1], w[0])
plt.show()

분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.

[[ 3.76686801]
 [-2.50677558]]

아울러 정규방정식은 다음과 같습니다.

   

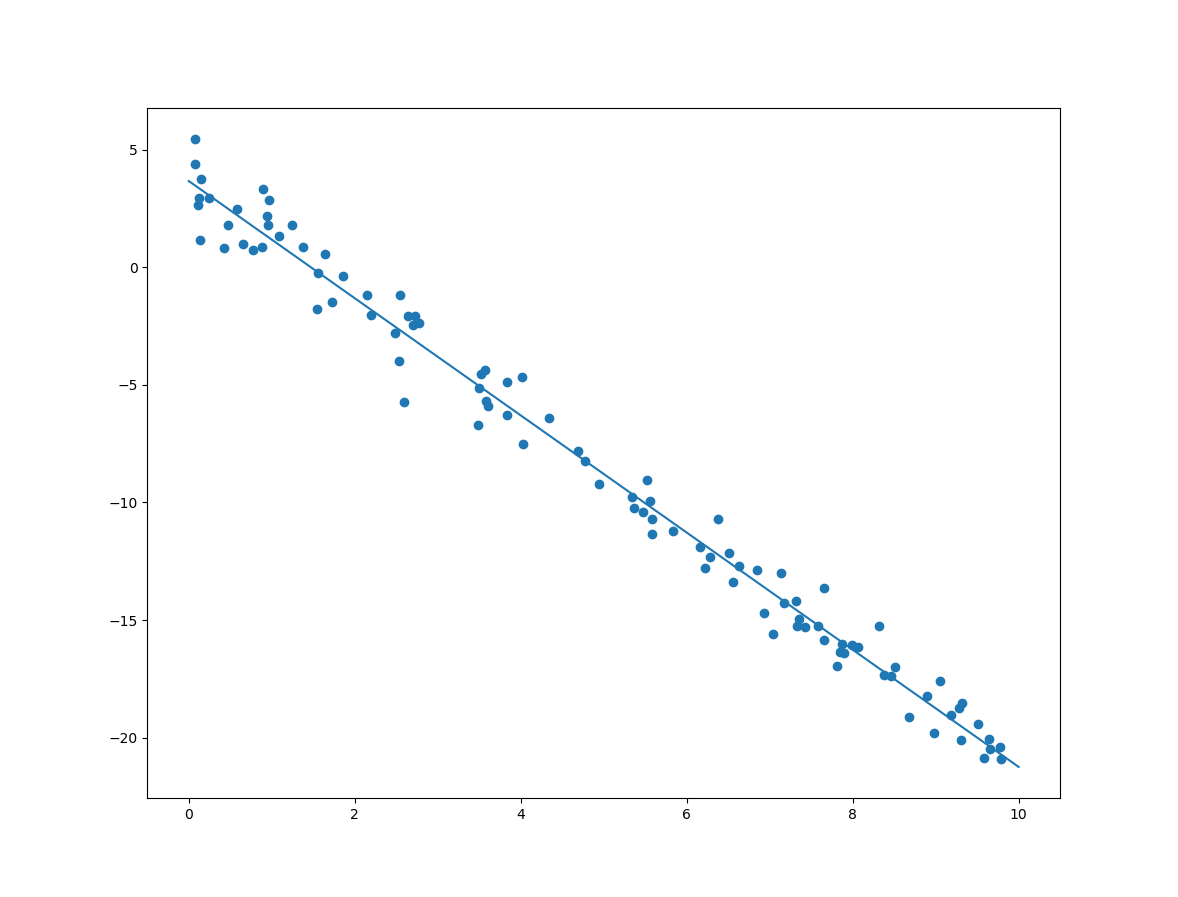
다음은 사이킷런에서 제공하는 LinearRegression 클래스를 이용한 방법입니다.

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
w = [model.intercept_[0], model.coef_[0][0]]
print(w)

plt.scatter(X, y)
drawLine(w[1], w[0])
plt.show()

분석된 절편과 기울기에 대한 출력 및 결과 모델의 선형은 다음과 같습니다.

[[ 3.69686801]
 [-2.50677558]]

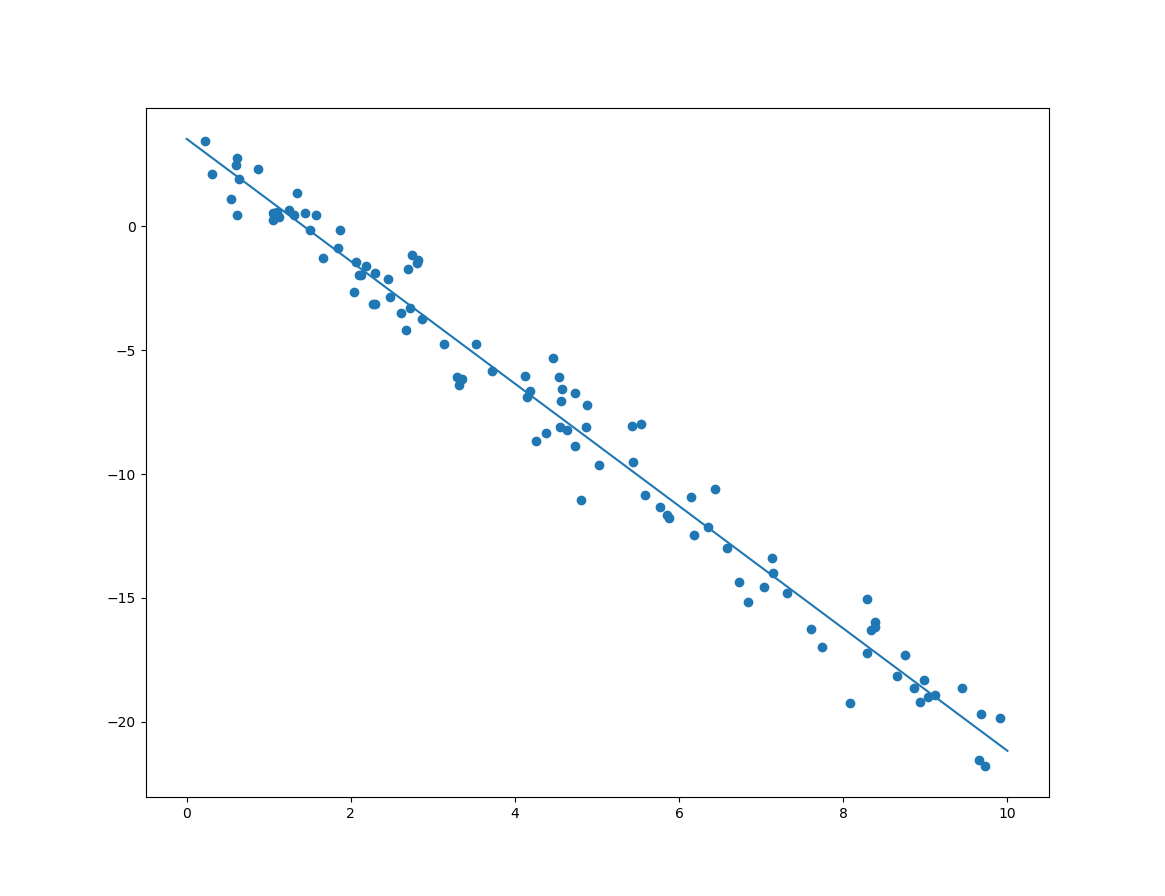
위의 코드에서 절편과 기울기를 통해 그래프를 그리는 함수인 drawLine은 다음과 같습니다.

def drawLine(m, b):
    X = np.arange(0, 11)
    y = [m * x + b for x in X]
    plt.plot(X, y)

이 글은 한빛미디어의 핸즈온 머신러닝을 수업자료로써 파악하면서 이해한 바를 짧게 요약한 글입니다. 요즘 이 책을 통해 머신러닝을 다시 접하고 있는데, 체계적이고 좋은 내용을 제공하고 있고, 나 자신을 위한 보다 명확한 이해를 돕고자 이 글을 작성 작성합니다. 요즘 제가 블로그에 올리는 머신러닝 관련 글은 대부분 이 책의 내용에 대한 나름대로의 해석을 토대로 합니다. 보다 자세한 내용은 해당 도서를 참고하기 바랍니다.

이글은 훈련된 예측 모델을 평가하기 위한 지표인 정밀도, 재현률, F1에 대한 내용입니다. 이러한 평가 지표는 혼돈행렬이라는 데이터를 토대로 계산되는데요, 먼저 혼돈행렬을 구하기 위해 학습 데이터셋이 필요하며, 0~9까지의 숫자를 손으로 작성한 MINIST를 사용하고, 이 손글씨가 7인지에 대한 예측 모델을 예로 합니다. MNIST 데이터셋을 다운로드 받고, 레이블 데이터를 재가공합니다.

from sklearn.datasets import fetch_openml
import numpy as np

mnist = fetch_openml('mnist_784', version=1, data_home='D:/__Temp__/_')

X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_7 = (y_train == 7)
y_test_7 = (y_test == 7)

예측 모델은 SGDClassifier를 사용합니다.

from sklearn.linear_model import SGDClassifier

model = SGDClassifier(random_state=3224)

혼돈 행렬을 얻기 위해 다음 코드를 실행합니다.

from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix

y_train_pred = cross_val_predict(model, X_train, y_train_7, cv=3)
cf = confusion_matrix(y_train_7, y_train_pred)
print(cf)

[[53223   512]
 [  726  5539]]

cross_val_predict 함수는 아직 전혀 학습이 되지 않은 모델을 지정된 교차검증 수만큼 학습시킨 뒤 예측값을 반환합니다. 이렇게 얻은 예측값과 실제 값을 비교해서 얻은 혼돈행렬의 결과에 대한 상세한 이미지는 아래와 같습니다.

위의 그림에서 표에 담긴 4개의 값은 발생횟수입니다. TN과 TP의 값은 옳바르게 예측한 횟수이고 FN과 FP는 잘못 예측한 횟수입니다. 즉, FN과 FP가 0일때 모델은 완벽하다는 의미입니다.

이제 위의 혼돈행렬에서 정밀도(Precision)와 재현률(Recall), F1점수에 대한 수식은 다음과 같습니다.

   

정밀도와 재현률이 서로 상반관계에 있습니다. 즉, 정밀도가 높으면 재현률이 떨어지며 재현률이 높아지면 정밀도가 떨어지는 경향이 있습니다. F1은 이런 상반관계에 있는 정밀도와 재현률을 묶어 평가하고자 하는 지표입니다.

비록 정밀도와 재현률, F1점수는 매우 단순해 계산하기 쉬우나 다음의 코드를 통해서도 쉽게 얻을 수 있습니다.

from sklearn.metrics import precision_score, recall_score, f1_score
p = precision_score(y_train_7, y_train_pred)
print(p)
r = recall_score(y_train_7, y_train_pred)
print(r)
f1 = f1_score(y_train_7, y_train_pred)
print(f1)

0.9153858866303091
0.8841181165203511
0.8994803507632347