이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_video/py_bg_subtraction/py_bg_subtraction.html 입니다.
배경 빼냄(Background Subtraction)은 많은 비전(Vision) 기반의 어플리케이션에서 중요한 처리입니다. 예를들어서, 고정 카메라에서 찍은 영상을 통해 몇명의 방문자가 방을 들어가고 나왔는지의 횟수를 센다거나, 교통 카메라에서 찍은 영상에서 차량의 정보를 추출하는 경우 등입니다. 이런 모든 경우에, 사람이나 차량을 추출해야 합니다. 기술적으로 변하지 않는 배경에서 움직이는 전경을 추출할 필요가 있습니다.
만약 배경만 가진 이미지라면, 즉 방문자나 차량이 전혀 없는 방이나 도로라면, 이것은 쉬운 작업입니다. 그러나 대부분의 경우에, 이렇지 않으므로 어떤 이미지든 배경을 추출할 필요가 있습니다. 만약 그림자까지 고려한다면 좀더 복잡해 집니다. 이동하는 그림자로 인해 배경을 전경으로 간주될 수 있기 때문입니다.
몇가지 알고리즘을 이런 목적을 위해 소개합니다. OpenCV에서는 3가지 알고리즘을 구현하였으며, 사용하기 쉽게 제공합니다. 하나씩 살펴보면..
먼저 BackgroundSubtractorMOG 알고리즘으로,가우시안 분산값 K(K=3~5)의 홉합에 의해 각 배경 픽셀을 구성하는 방법입니다. 홉합의 가중치는 장면에서 이들 색상값들이 머무르고 있는 시간 비율입니다. 배경으로써 판단될 수 있는 색상은 더 오랜 시간동안 변하지 않는 것입니다.
이 알고리즘의 구현은 cv2.bgsegm.createBackgroundSubtractorMOG()이며, 선택된 인자로써, 연산 인력의 길이, 가우시안 믹스쳐(혼합)의 개수, 임계값 등인데, 이는 모두 기본값으로 설정되어져 있습니다. 비디오의 각 프레임을 얻는 루프에서 apply 매서드를 호출하여 전경에 대한 마스크를 얻습니다. 예제는 다음과 같습니다.
import numpy as np
import cv2
cap = cv2.VideoCapture('./data/vtest.avi')
fgbg = cv2.bgsegm.createBackgroundSubtractorMOG()
while(1):
ret, frame = cap.read()
fgmask = fgbg.apply(frame)
cv2.imshow('frame',fgmask)
k = cv2.waitKey(30) & 0xff
if k == 27:
break
cap.release()
cv2.destroyAllWindows()
결과는 다음과 같습니다.
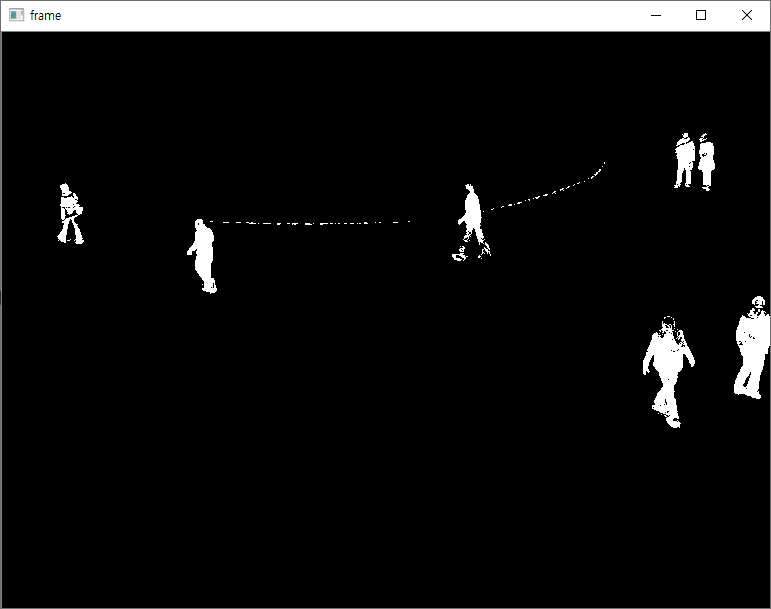
다음 알고리즘은 BackgroundSubtractorMOG2로써, 장면에서의 조도값이 변경되는 경우에도 좋은 결과를 제공하며, 그림자에 대한 처리가 가능합니다. 또한 BackgroundSubtractorMOG와 다르게 각 픽셀마다 가우시안 분산값의 개수를 적당한 값을 선택해 줍니다.
이 알고리즘은 cv2.createBackgroundSubtractorMOG2() 함수로 실행 가능하며, detectShadows 선택 인자를 통해 그림자에 대한 처리 여부를 결정할 수 있는데, 기본값은 True입니다. 그림자는 마스크 결과로 회색으로 마킹됩니다. 아래는 예제 코드입니다.
import numpy as np
import cv2
cap = cv2.VideoCapture('./data/vtest.avi')
fgbg = cv2.createBackgroundSubtractorMOG2()
while(1):
ret, frame = cap.read()
fgmask = fgbg.apply(frame)
cv2.imshow('frame',fgmask)
k = cv2.waitKey(30) & 0xff
if k == 27:
break
cap.release()
cv2.destroyAllWindows()
아래는 실행 결과입니다.

마지막으로 BackgroundSubtractorGMG 알고리즘입니다. 이 알고리즘은 정적인 배경 이미지 추정과 픽셀 당 Bayesian 분할을 조합하는 방식입니다. 일단 이 알고리즘은 동영상의 처음 몇 개의 프레임(기본값 120)을 배경 모델링을 위해 사용합니다. (그래서 이 알고리즘을 사용하면 처음 실행시 까만 화면만 표시됩니다.) 그리고 이를 Bayesian 추정을 사용하여 전경이라고 판단되는 것을 찾아 냅니다. 이러한 판단은 조정이 가능한데, 더 새로운 관측이 조도값이 변경되는 것을 수용할 수 있도록 더 높은 가중치를 갖습니다. 전경에 대한 마스크 이미지에 대한 잡음을 제거하기 위해 Closing과 Opening과 같은 Morphological 필터링 연산이 수행되는데, Opening이 더 잡음을 잘 제거합니다. 예제는 다음과 같습니다.
import numpy as np
import cv2
cap = cv2.VideoCapture('./data/vtest.avi')
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(3,3))
fgbg = cv2.bgsegm.createBackgroundSubtractorGMG()
while(1):
ret, frame = cap.read()
fgmask = fgbg.apply(frame)
fgmask = cv2.morphologyEx(fgmask, cv2.MORPH_OPEN, kernel)
cv2.imshow('frame',fgmask)
k = cv2.waitKey(30) & 0xff
if k == 27:
break
cap.release()
cv2.destroyAllWindows()
결과는 다음과 같습니다.