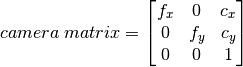[카테고리:] OpenCV

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_calib3d/py_pose/py_pose.html 입니다.

이전 글은 카메라 보정에 대한 내용으로, 카메라 메트릭스와 왜곡 계수 등을 구했습니다. 주어진 패턴 이미지를 통해 우리는 이미지 안의 패턴의 자세를 계산하기 위한 정보를 이용할 수 있고 객체가 공간상에 어떻게 놓여있는지 파악할 수 있습니다. 평면 객체에 대해서는, Z값을 0으로 가정한다면.. 이미지의 이러한 객체에 대한 자세 문제는 카메라가 공간 상에 어떻게 위치해 있는지의 문제가 됩니다. 그래서, 만약 공간 상에 객체가 어떻게 놓여 있는지를 안다면, 3차원 효과를 시뮬레이션하기 위해 이미지 상에 2차원 도형을 그려 넣을 수 있습니다.

우리의 목표는 체스판의 첫번째 코너 지점 위에 3차원 좌표축(X, Y, Z 축)을 그려 넣는 것입니다. X 측은 파랑색으로, Y축은 초록색으로 Z축은 빨간색으로 그려 봅시다. 그래서 효과면에서 볼 때, Z축은 체스판 상에 수직으로 느껴져야 합니다.

가장 먼저, 이전 카메라 보정 결과로부터 카메라 행렬과 왜곡계수를 계산해 봅시다.

import numpy as np
import cv2
import glob

criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

objpoints = []
imgpoints = []

images = glob.glob('./data/chess/*.jpg')

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

    ret, corners = cv2.findChessboardCorners(gray, (7,6),None)

    if ret == True:
        objpoints.append(objp)

        corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        imgpoints.append(corners2)

ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)

draw라는 사용자 정의 함수를 만들텐데, 이 함수는 cv2.findChessboardCorners() 함수를 통해 구한 체스판의 코너점과 축의 포인트를 인자로 받아 3차원 축을 그립니다.

def draw(img, corners, imgpts):
    corner = tuple(corners[0].ravel())
    img = cv2.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)
    img = cv2.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)
    img = cv2.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)
    return img

축의 포인트를 위한 변수를 정의할 것인데, 이 변수는 축을 그리기 위한 3차원 공간 상의 포인트입니다. 길이 3(단위는 체스보드의 크기를 기반으로 함)만큼을 축의 길이로 정합니다. 그래서 X축의 선은 (0,0,0)-(3,0,0)으로, Y축의 선은 (0,0,0)-(0,3,0)으로, Z축은 (0,0,0)-(0,0,-3)인데, 음수인 이유는 카메라의 방향을 나타내기 위함입니다.

axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)

자, 이제 각 이미지를 로드하고 이미 상의 체스판의 7×6 그리드를 찾습니다. 만약 발견되면, 이를 Subcorner 픽셀로 정제합니다. cv2.solvePnPRansac() 함수를 사용해 회전과 이동을 계산합니다. 일단 이러한 변환 행렬이 계산되면, 이를 이용해 이미지 평면 상의 축의 포인트들을 투영합니다. 간단히 말해서, 3차원 상의 좌표 (3,0,0), (0,3,0), (0,0,3)에 해당하는 이미지 상의 좌표를 얻는 것입니다. 이 3개의 좌표가 얻어졌다면 앞서 정의한 draw 함수를 통해 그립니다.

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,  cv2.COLOR_BGR2GRAY)
    ret, corners = cv2.findChessboardCorners(gray, (7,6),None)

    if ret == True:
        corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

        # Find the rotation and translation vectors.
        _, rvecs, tvecs, inliers = cv2.solvePnPRansac(objp, corners2, mtx, dist)

        # project 3D points to image plane
        imgpts, jac = cv2.projectPoints(axis, rvecs, tvecs, mtx, dist)

        img = draw(img, corners2, imgpts)
        cv2.imshow('img',img)
        k = cv2.waitKey(500)

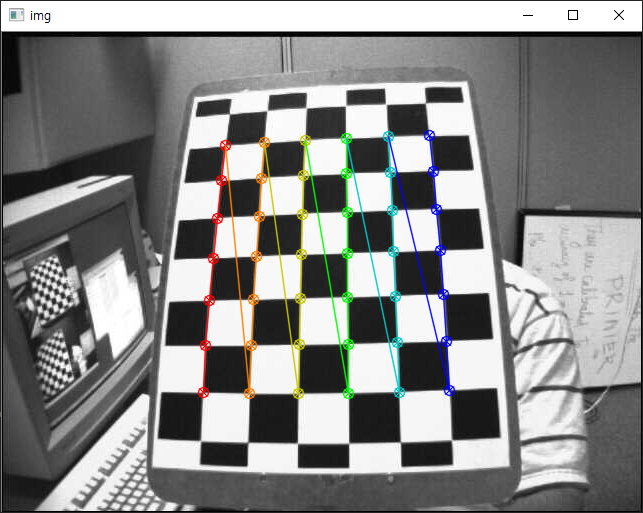
아래 그림은 위 예제의 실행 시 표시되는 영상 중 하나입니다.

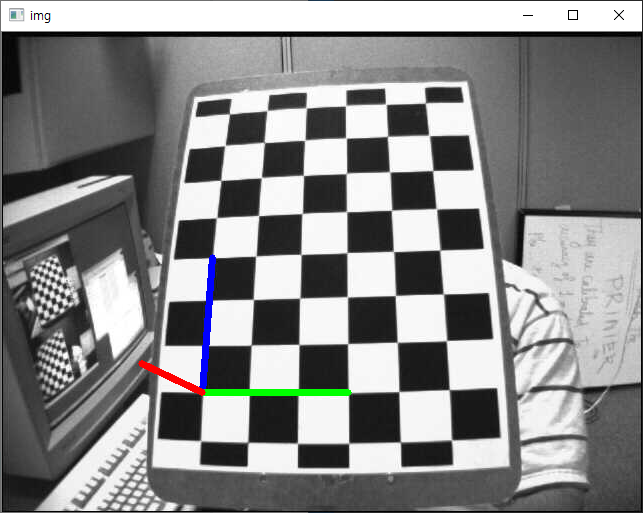
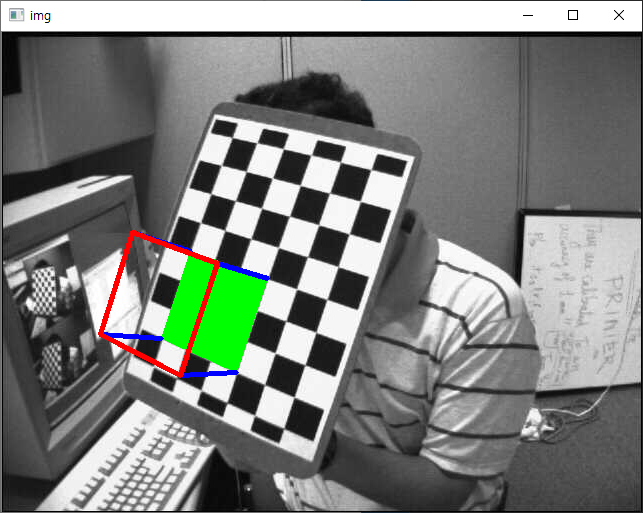
이제, 3차원 축을 파악했으니, draw 함수를 변형해서 3차원 큐브를 이미지에 표시하겠습니다. 수정된 draw 함수는 다음과 같습니다.

def draw(img, corners, imgpts):
    imgpts = np.int32(imgpts).reshape(-1,2)

    # draw ground floor in green
    img = cv2.drawContours(img, [imgpts[:4]],-1,(0,255,0),-3)

    # draw pillars in blue color
    for i,j in zip(range(4),range(4,8)):
        img = cv2.line(img, tuple(imgpts[i]),tuple(imgpts[j]),(255),3)

    # draw top layer in red color
    img = cv2.drawContours(img, [imgpts[4:]],-1,(0,0,255),3)

    return img

변경된 draw 함수에 맞게 기존의 axis 변수도 큐브를 구성하는 8개의 모서리 좌표에 맞게 변경됩니다.

axis = np.float32([[0,0,0], [0,3,0], [3,3,0], [3,0,0],
                   [0,0,-3],[0,3,-3],[3,3,-3],[3,0,-3]])

실행해보면, 그 결과 중 하나의 이미지는 아래와 같습니다.

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_calib3d/py_calibration/py_calibration.html 입니다.

카메라나 비디오 영상의 왜곡 현상과 카메라의 내부, 외부 파라메터에 대해 학습하며, 이런 파라메터를 얻는 방법과 이미지의 왜곡 현상을 제거하는 내용을 설명합니다.

현대의 값 싼 소형 카메라(노트북이나 스마트폰에 장착된 개미 눈크기 만한 렌즈같은..)은 상당한 이미지의 왜곡을 발생시킵니다. 주요한 왜곡은 방사 왜곡과 탄젠티얼(Tangential) 왜곡이 있습니다.

방사 왜곡으로 인해, 아래의 그림처럼 반듯한 형상이 휘어지게 됩니다. 이런 현상은 이미지의 중심으로부터 멀어질수록 심해집니다.

위와 같은 왜곡 현상은 아래의 공식을 이용하면 해결할 수 있습니다.

유사하게, 또 다른 왜곡은 탄젠티얼 왜곡이며 이는 카메라의 렌즈가 이미지 평면에 완전하게 수평이 아닌 이유로 발생합니다. 이미지의 어떤 영역은 예상밖으로 더 가깝게 보이기도 합니다. 이는 아래의 공식으로 해결할 수 있습니다.

요약하면, 5개의 파라메터가 필요한데, 이 파라메터를 아래처럼 왜곡 계수라고 합니다.

추가적으로, 카메라의 내부(Intrinsic) 및 외부(Extrinsic) 파라메터에 대한 몇가지 더 많은 정보가 필요합니다. 내부 파라메터는 카메라에 특정되어 있습니다. 먼저 초점 길이(), 광학 중심() 등입니다. 이들을 카메라 메트릭스라고 부릅니다. 이는 오직 카메라의 특성에 의존하므로, 한번 계산되면 변하지 않으므로 계속 사용할 수 있습니다. 아래의 행렬과 같습니다.

외부 파라메터는 3차원 포인트를 좌표체계로 이동하는 회전 및 이동 벡터에 해당합니다.

스테레오 어플리케이션에서는 이러한 왜곡을 가장 먼저 보정해야 합니다. 이들 모든 파라메터를 구하기 위해, 해야할 것은 잘 정의된 패턴(예를들어, 체스판)이 담긴 샘플 이미지들을 제공하는 것입니다. 이 이미지 내부에 지정된 지점들(체스보드의 사각형 모서리)을 찾습니다. 이미 알고 있는 실세계에서의 좌표가 이미지의 어디에 해당하는지를 파악할 수 있는 지점입니다. 이러한 데이터를 가지고, 몇가지 수학적 문제가 왜곡 계수를 얻기 위한 바탕 위에서 해결됩니다. 지금까지가 전체 이야기에 대한 요약입니다. 카메라 보정을 위한 더 좋은 결과를 위해 최소한 10개의 패턴 이미지가 필요합니다.

앞서 언급했던 것처럼, 카메라 보정을 위해 최소한 10개의 테스트 패턴 이미지가 필요하다고 했습니다. 이해를 돕기 위해, 체스 보드에 대한 하나의 이미지에 집중하겠습니다. 카메라 보정을 위해 필요한 중요한 입력 데이터는 3차원의 실세계의 지점에 대한 집합과 이 집합에 대한 2차원 이미지 상의 지점 집합입니다. 2차원 이미지 지점은 이미지로부터 쉽게 발결할 수 있기만 하면 됩니다. (이들 이미지 지점들은 2개의 검정색 사각형이 맞닿은 위치가 됩니다)

실세계 공간에 대한 3차원 지점은 무엇일까요? 이들 이미지는 정적인 카메라로부터 촬영되었고 체스 보드는 다른 위치와 방향에 놓여 있습니다. 그래서 우리는 좌표를 파악할 필요가 있습니다. 그러나 단순화시키기 위해, 체스판이 XY 평면을 유지하고 있다고 말할 수 있어야 합니다(즉 항상 Z=0). 그리고 카메라는 이에 따라 움직이고 있습니다. 이러한 중요한 가정이 오직 X, Y값만을 계산하는 것으로 단순화시켜 줍니다. 이제 X,Y 값에 대해, 지점의 위치를 나타내는 (0,0), (1,0), (2,0), … 형식으로 단순하게 전달할 수 있습니다. 이 경우, 결과는 체스판에서의 사각형의 크기 축척으로 구해집니다. 그러나 만약 이 사각형의 크기를 알고 있다면(30mm라고 말할 수 있다면), mm 단위 결과로써 (0,0), (30,0), (60,0), …처럼 전달할 수 있습니다.

실세계에서의 3D 지점을 객체 지점이라고하고, 2D 이미지 지점을 이미지 지점이라고 합니다.

체스보드의 패턴을 찾기 위해, cv2.findChessboardCorners() 함수를 사용합니다. 또한 찾고자 하는 패턴이 어떤 형태인지, 즉 8×8 격자인지 5×5격자인지 등과 같이 말입니다. 이 예제에서는 7×6 격자입니다. 이 함수는 코너 지점과 패턴이 발견되었는지의 여부를 반환합니다. 이들 코너 지점들은 위치상 왼쪽에서 오른쪽으로, 위에서 아래로 정렬되어 있습니다. 체스판과 같은 이미지 대신에 원형 그리고 이미지를 사용할 수도 있는데, 이때는 cv2.findCirclesGrid()를 사용합니다.

일단 코너를 발견하면, cv2.cornerSubPix() 함수를 사용하여 정확도를 높일 수 있습니다. 또한 cv2.drawChessboardCorners() 함수를 사용해 코너 결과를 그릴 수 있습니다. 지금까지의 이야기에 대한 전체 코드는 아래와 같습니다.

import numpy as np
import cv2
import glob

# termination criteria
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.

images = glob.glob('./data/chess/*.jpg')

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

    # Find the chess board corners
    ret, corners = cv2.findChessboardCorners(gray, (7,6),None)

    # If found, add object points, image points (after refining them)
    if ret == True:
        objpoints.append(objp)

        corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        imgpoints.append(corners2)

        # Draw and display the corners
        img = cv2.drawChessboardCorners(img, (7,6), corners2,ret)
        cv2.imshow('img',img)
        cv2.waitKey(500)

cv2.destroyAllWindows()

동일한 카메로 위치와 각도에서, 서로 다른 체스판의 위치로 촬영된 13개의 이미지를 활용하여 패턴을 검출하는데, 실행 결과 중 한컷은 다음과 같습니다.

패턴 검출을 통해 객체 지점(objpoints)과 이미지 지점(imgpoints)을 파악했으므로, 이를 이용해 왜곡된 촬영 영상을 보정할 수 있습니다. 보정 전에 cv2.getOptimalNewCameraMatrix() 함수를 이용해 먼저 카메라 메트릭스를 구해야 합니다. 이 함수는 카메라 메트릭스, 왜곡 계수, 회전/이동 벡터 등이 반환됩니다. 이 코드는 위의 예제 코드에서 36번째 줄의 for 문 외부에 위치합니다.

ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)

이제 이미지의 왜곡을 제거할 수 있는데, OpenCV에서는 2가지 방법을 제공합니다. 그러나 먼저 왜곡을 제거하기에 앞서 cv2.getOptimalNewCameraMatrix() 함수를 사용하여 카메라 메트릭스를 개선할 수 있습니다. 이 함수의 스케일링 인자 alpha = 0 일 경우, 원치않는 픽셀을 최소로 갖는 보정된 이미지가 얻어지는데, 코너 지점의 픽셀들이 제거될 수도 있습니다. alpha = 1일 경우 모든 픽셀은 유지됩니다. 이 함수는 또한 결과를 자르는데 사용할 수 있는 이미지 ROI를 반환합니다. 13개의 샘플 이미지 중 왜곡 현상을 제거할 하나를 사용해 이미지의 크기를 얻고, 카메라 메트릭스를 얻는 코드는 다음과 같습니다.

img = cv2.imread('./data/chess/left12.jpg')
h,  w = img.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))

위에서 왜곡을 제거하는 방법이 OpenCV에서는 2가지를 제공한다고 했는데, 첫번재는 다음과 같습니다.

dst = cv2.undistort(img, mtx, dist, None, newcameramtx)

x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)

위와 동일한 결과를 제공하는 또 다른 방법은 다음과 같습니다.

mapx,mapy = cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)
dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)

x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)

실행해보면, 먼저 13장의 샘플 이미지를 통해 패턴을 분석하고, 분석된 패턴을 통해 카메라 메트릭스가 얻어지며 이 메트릭스를 개선한 뒤 최종적으로 왜곡된 부분을 제거해 calibresult.png 파일로 저장합니다. calibresult.png 파일은 다음과 같이 왜곡이 제거된 것을 볼 수 있습니다.

앞서 계산한 카메라 행렬과 왜곡계수들은 저장해두고 재활용할 수 있습니다.

왜곡 제거는 이미지의 프로젝션입니다. 이 왜곡 제거 시 수행된 프로젝션에 발생하는 오차가 얼마인지를 알기 위해 cv2.projectPoints() 함수가 사용됩니다. 결과적으로 얻어지는 값이 0에 가까울수록 정확한 것입니다.

tot_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    tot_error += error

print("total error: ", tot_error/len(objpoints))