[카테고리:] OpenCV

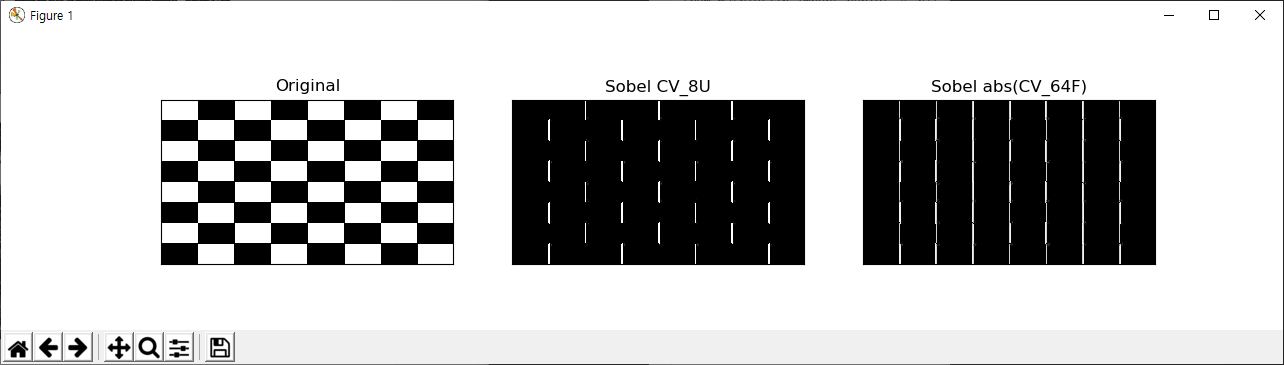
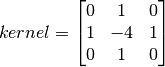이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_pyramids/py_pyramids.html#pyramids 입니다.

동일한 영상에 대해서 이미지의 크기를 50% 크기만큼 연속적으로 줄이거나 늘려 생성된 이미지 집합을 이미지 피라미드라고 합니다. OpenCV에서 제공하는 이미지 피라미드 관련 함수는 cv2.pyrDown과 cv2.pryUp 인데, cv2.pyrDown 함수는 입력 이미지를 50% 크기로 줄인 이미지를 생성해 반환하고 cv2.pryUp은 입력 이미지를 200% 크기로 확대한 이미지를 생성해 반환합니다. 먼저 cv2.pryDown 함수의 예를 살펴보면..

import cv2

img0 = cv2.imread('./data/apple.jpg')
img1 = cv2.pyrDown(img0)
img2 = cv2.pyrDown(img1)
img3 = cv2.pyrDown(img2)

cv2.imwrite('img0.jpg', img0)
cv2.imwrite('img1.jpg', img1)
cv2.imwrite('img2.jpg', img2)
cv2.imwrite('img3.jpg', img3)

위의 예제에서 apple.jpg 이미지는 512×512 크기의 이미지인데, img1은 256×256으로.. img2는 128×128으로.. img3는 64×64로 크기가 축소된 이미지가 저장됩니다. 다음은 cv2.pryUp 함수에 대한 예제입니다.

import cv2

img0 = cv2.imread('./data/apple.jpg')
img1 = cv2.pyrUp(img0)
img2 = cv2.pyrUp(img1)
img3 = cv2.pyrUp(img2)

cv2.imwrite('img0.jpg', img0)
cv2.imwrite('img1.jpg', img1)
cv2.imwrite('img2.jpg', img2)
cv2.imwrite('img3.jpg', img3)

위의 예제 역시 유사하게 apple.jpg 이미지는 512×512이고, img1.jpg는 1024×1024로.. img2는 2048×2048로.. img3는 4096×4096의 크기로 확대되어 저장됩니다.

지금까지의 이미지 피라미드는 Gaussian Pyramid 라고 하는데, Laplacian Pyramids 라는 종류의 피라미드가 있습니다. Laplacian Pyramids는 Gaussian Pyramid로부터 생성되며 OpenCV에서 이를 위해 별도로 제공하는 함수는 없습니다. Gaussian Pyramid는 Gaussian Pyramid로부터 생성된 이미지들에 대한 외곽선 추출 이미지들의 집합입니다.

이미지 피라미드에 대한 응용 중 하나로 Image Blending이 있습니다. 하나의 예제 코드를 언급할텐데, 그 예제 코드의 결과를 먼저 보면..

A 영상과 B 영상의 반씩 혼합하여 ls_과 real이라는 새로운 영상을 만드는 것인데 real은 단순히 A와 B 각각 좌우에 대한 이미지를 붙인 이미지이지만 ls_는 A와 B를 붙인 경계가 날카롭지 않고 자연스럽습니다. 이런 ls_를 생성하는 절차는 다음과 같습니다.

1. A와 B 이미지를 로딩한다.
2. A와 B에 대한 Gaussian Pyramid를 생성한다. (6개 정도)
3. Gaussian Pyramid로 생성된 결과로부터 Laplacian Pyramids를 생성한다.
4. Laplacian Pyramids의 각 레벨에 대한 A와 B 영상의 반절씩 조합한다.
5. 앞서 조합한 이미지 피라미드로부터 원본 이미지를 다시 생성한다.

위의 절차에 대한 코드는 다음과 같습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

A = cv2.imread('./data/apple.jpg')
B = cv2.imread('./data/orange.jpg')
 
# generate Gaussian pyramid for A
G = A.copy()
gpA = [G]
for i in range(6):
    G = cv2.pyrDown(G)
    gpA.append(G)

# generate Gaussian pyramid for B
G = B.copy()
gpB = [G]
for i in range(6):
    G = cv2.pyrDown(G)
    gpB.append(G)

# generate Laplacian Pyramid for A
lpA = [gpA[5]]
for i in range(5,0,-1):
    GE = cv2.pyrUp(gpA[i])
    L = cv2.subtract(gpA[i-1],GE)
    lpA.append(L)

# generate Laplacian Pyramid for B
lpB = [gpB[5]]
for i in range(5,0,-1):
    GE = cv2.pyrUp(gpB[i])
    L = cv2.subtract(gpB[i-1],GE)
    lpB.append(L)

# Now add left and right halves of images in each level
LS = []
xxx = 0
for la,lb in zip(lpA,lpB):
    rows,cols,dpt = la.shape
    ls = np.hstack((la[:,0:int(cols/2)], lb[:,int(cols/2):]))
    LS.append(ls)

# now reconstruct
ls_ = LS[0]
for i in range(1,6):
    ls_ = cv2.pyrUp(ls_)
    ls_ = cv2.add(ls_, LS[i])

# image with direct connecting each half
real = np.hstack((A[:,:int(cols/2)],B[:,int(cols/2):]))

b, g, r = cv2.split(A)
A = cv2.merge([r,g,b])
plt.subplot(2,2,1), plt.imshow(A), plt.title('A'), plt.xticks([]), plt.yticks([])

b, g, r = cv2.split(B)
B = cv2.merge([r,g,b])
plt.subplot(2,2,2), plt.imshow(B), plt.title('B'), plt.xticks([]), plt.yticks([])

b, g, r = cv2.split(ls_)
ls_ = cv2.merge([r,g,b])
plt.subplot(2,2,3), plt.imshow(ls_), plt.title('ls_'), plt.xticks([]), plt.yticks([])

b, g, r = cv2.split(real)
real = cv2.merge([r,g,b])
plt.subplot(2,2,4), plt.imshow(real), plt.title('real'), plt.xticks([]), plt.yticks([])

plt.show()

이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_gradients/py_gradients.html 와 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_canny/py_canny.html#canny 입니다.

이 글에서는 이미지의 변화도(Gradients)에 따른 가장자리를 추출하는 내용에 대해 정리합니다.

이미지의 변화도에 따른 가장자리 추출 방법은 Sobel 방법, Scharr 방법, Laplacian 방법이 있습니다. 먼저 Sobel과 Scharr은 변화도를 추출할 방향을 x와 y축으로 지정할 수 있습니다. 그리고 Sobel의 경우 커널 행렬의 크기를 지정할 수 있는 인자가 있지만 Scharr는 필터 행렬의 크기를 지정하는 인자가 없습니다. Laplacian은 변화도의 추출 방향을 지정하는 방식이 아니고 전체 방향으로의 가장자리를 추출하며 커널 행렬의 크기를 지정할 수 있는데 이 행렬 크기를 1로 지정하면 아래의 행렬이 사용됩니다.

코드의 예는 아래와 같습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('./data/sudoku-original.jpg', 0)

laplacian = cv2.Laplacian(img,cv2.CV_8U,ksize=5)
sobelx = cv2.Sobel(img,cv2.CV_8U,1,0,ksize=5)
sobely = cv2.Sobel(img,cv2.CV_8U,0,1,ksize=5)

plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])

plt.show()

결과는 다음과 같습니다.

위의 코드에서 cv2.Laplacian과 cv2.Sobel 함수의 2번째 인자에 결과 데이터의 타입을 cv2.CV_8U로 지정하고 있습니다. 이 데이터 타입의 문제는 정보의 소실이 발생한다는 것인데, 검정색에서 하얀색으로 변화도는 음수값이므로 음의 경사라고 하고 하얀색에서 검정색으로 변화도는 양의 값이므로 양의 경사라고 합니다. cv2.CV_8U로 지정하면 음의 값은 모두 0으로 변환되어 버리게 되는데, 이처럼 음의 변화도에 대한 정보도 유지하기 위해서는 결과 데이터 타입을 정밀도가 더 높으면서 부호값을 가지는 cv2.CV_16S, cv2.CV_64F로 지정한 뒤에 다시 cv2.CV_8U로 변환하는 것을 추천합니다. 이에 대한 예제 코드가 다음과 같습니다.

지금까지 살펴본 이미지에 대한 Gradients(변화도)는 가장자리(Edge) 검출을 위한 인자로 활용되는데, 가장 유명한 가장자리 검출을 위한 방법은 Canny Egde Detection이며 예제 코드는 다음과 같습니다.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('./data/messi5.jpg', 0)
edges = cv2.Canny(img, 200, 255)

plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])

plt.show()

실행 결과는 다음과 같습니다.

6번 코드의 cv2.Canny 함수의 2번째와 3번째 각 픽셀이 가장자리 인지의 여부에 대한 기준값이 되는 minThresholdingValue, maxThresholdingValue입니다. 이값을 조정하여 원하는 수준의 가장자리를 검출을 조정할 수 있습니다.