FingerEyes-Xr for HTML5는 DeferableShapeDrawTheme 추상 클래스를 제공합니다. Deferable은 “미룰 수 있는”이라는 의미인데요. 수치지도 레이어를 그리기 위한 심벌의 지정을 미룬다는 의미입니다. 이 추상 클래스는 상속 받아 구현해야 하는 매서드는 /* void */ requestCondition: function (/* int */fid)입니다. 이 클래스의 목적에 대한 설명은 잠시 미루고 이 클래스를 상속받아 만든 예로써 MyDeferableShapeDrawTheme 클래스는 아래와 같습니다.
MyDeferableShapeDrawTheme = Xr.Class({
name: "MyDeferableShapeDrawTheme",
extend: Xr.theme.DeferableShapeDrawTheme,
construct: function() {
this.superclass();
this._ON_sds = new Xr.symbol.ShapeDrawSymbol();
this._ON_sds.markerSymbol(new Xr.symbol.ImageMarkerSymbol(
{ width: 16, height: 16, url: "images/gis/facility/OH_SW_ON.png" }));
this._OFF_sds = new Xr.symbol.ShapeDrawSymbol();
this._OFF_sds.markerSymbol(new Xr.symbol.ImageMarkerSymbol(
{ width: 16, height: 16, url: "images/gis/facility/OH_SW_OFF.png" }));
},
methods: {
/* void */ requestCondition: function (fid) {
var that = this;
var sql = "SELECT swstatcd FROM ecl_sw_p WHERE fid = " + fid;
var url = mg_MapLayers.GIS_HTTP_SERVER + "/Xr?sql|" + encodeURIComponent(sql) + "|mg_db|1"
$.ajax({
url: url,
dataType: "text",
type: "GET",
statusCode: {
200: function (response) {
// response 문자열 끝에 \0 문자를 제거
response = response.substr(0, response.length - 1);
var result = JSON.parse(response);
if (result.length == 1) {
if (result[0]["swstatcd"] === "ON") {
that.setSymbol(fid, that._ON_sds);
} else {
that.setSymbol(fid, that._OFF_sds);
}
}
}
}
});
}
}
});
위의 코드는 순수한 Javascript 코드이며, FingerEyes-Xr 방식의 클래스 정의입니다. 위의 코드에서 보이는 것처럼 3번 코드에서 Xr.theme.DeferableShapeDrawTheme 클래스는 확장한다고 명시되어 있고, 18번 코드에서 requestCondition 매서드를 구현하고 있습니다. 5번 코드가 생성자 함수인데요. 이 생성자에서는 2개의 이미지 심벌을 정의하고 있습니다. 이 2개의 이미지 심벌은 설비 따위에 대한 상태값으로 ON 상태의 이미지와 OFF 상태의 이미지를 나타냅니다. 이렇게 정의된 심벌은 18번 코드의 매서드인 requestCondition에서 사용되는데요. 이 requestCondition은 이름 그대로 “조건을 요청한다”라는 매서드로 그 구현 코드를 보면 어떤 SQL문을 서버측에 요청하고 있습니다. 그 요청 결과는 JSON으로 받게 되는데요. 34~38번 코드에서처럼 JSON 결과 중 swstatcd 필드의 값이 ON일때와 그 외의 값일때에 대해 setSymbol 매서드를 호출해 표현할 심벌을 지정해 줍니다.
이렇게 정의된 MyDeferableShapeDrawTheme 클래스는 수치지도 레이어를 생성하고 추가할때 사용되는데요. 아래의 예와 같습니다.
var lyr = new Xr.layers.ShapeMapLayer(layerId, ...); lyr.deferableTheme(new MyDeferableShapeDrawTheme());
이해를 돕고자 위의 코드가 적용된 실행 결과에 대한 지도 화면은 다음과 같습니다.
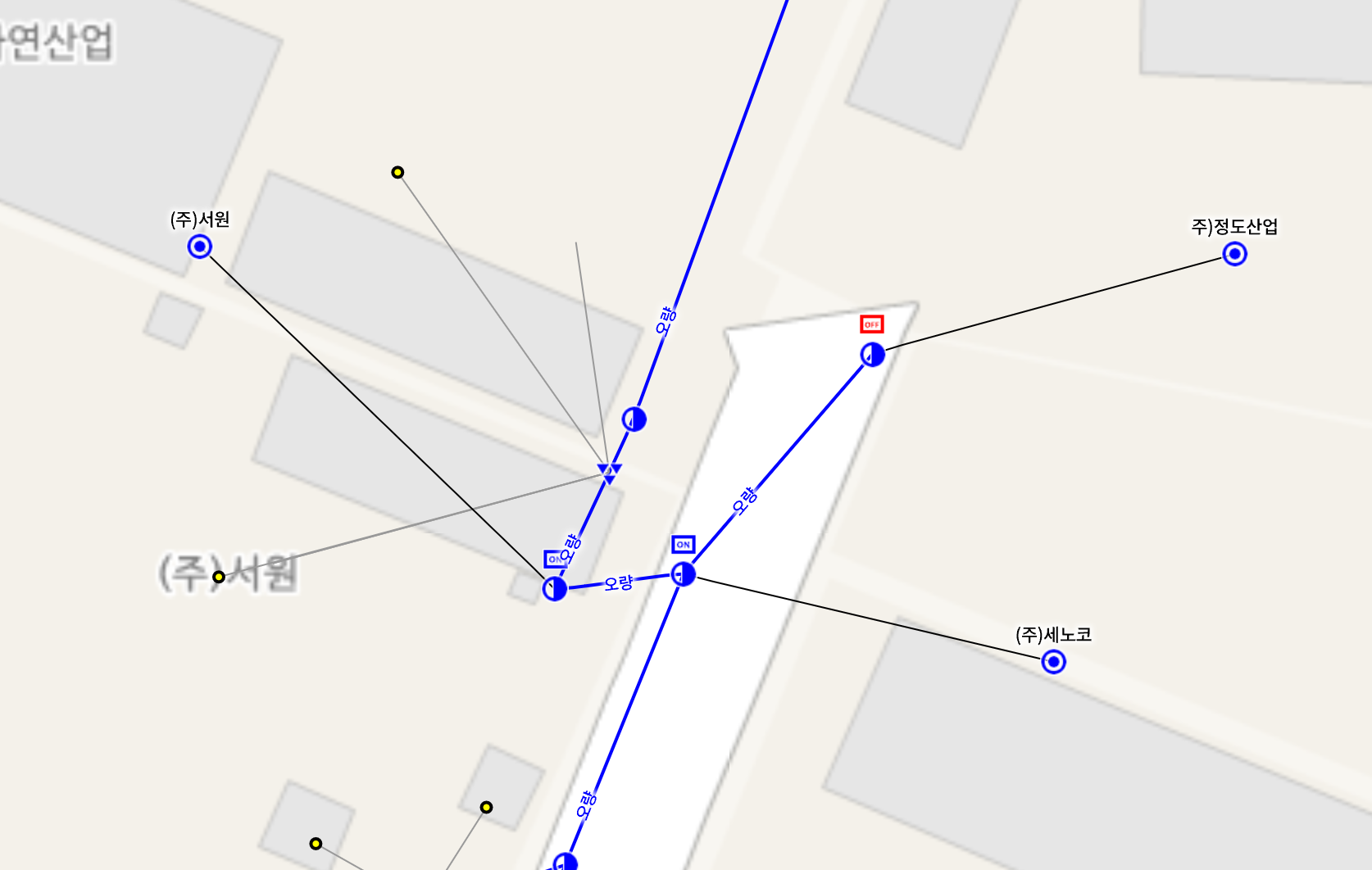
위의 지도 화면에서 파랑색의 ON 아이콘과 빨간색의 OFF 아이콘 심벌이 위의 코드를 통해 반영된 심벌 결과입니다.
그렇다면 이 클래스의 제공하는 이유는 무엇일까요? 일반적으로 GIS의 DB 구조를 살펴보면 공간 데이터와 속성 데이터가 동일한 DBMS의 동일한 Database 내에 존재하게 됩니다. 그러나 전체 시스템이 커지거나, 타 시스템와의 연계가 필요할 경우 도형 데이터와 속성 데이터가 전혀 다른 DBMS로 분리 구분되어 저장됩니다. 바로 이러한 환경에서도 공간 데이터와 다른 DBMS의 속성 데이터가 접목되어 유연하게 조합되어 활용될 수 있도록 하기 위해 제공되는 클래스가 바로 DeferableShapeDrawTheme입니다.
끝으로, ShapeDrawSymbol 클래스를 통한 심벌 정의 시에 Brush와 Pen에 대한 심벌의 정의 예는 아래와 같습니다.
this._ON_sds = new Xr.symbol.ShapeDrawSymbol();
this._sds.brushSymbol(new Xr.symbol.BrushSymbol({ color: 'red' }));
this._sds.penSymbol(new Xr.symbol.PenSymbol({ color: 'yellow', width: 2 }));
this._ON_sds.markerSymbol(new Xr.symbol.ImageMarkerSymbol(
{ width: 16, height: 16, url: "images/gis/facility/OH_SW_ON.png" }));