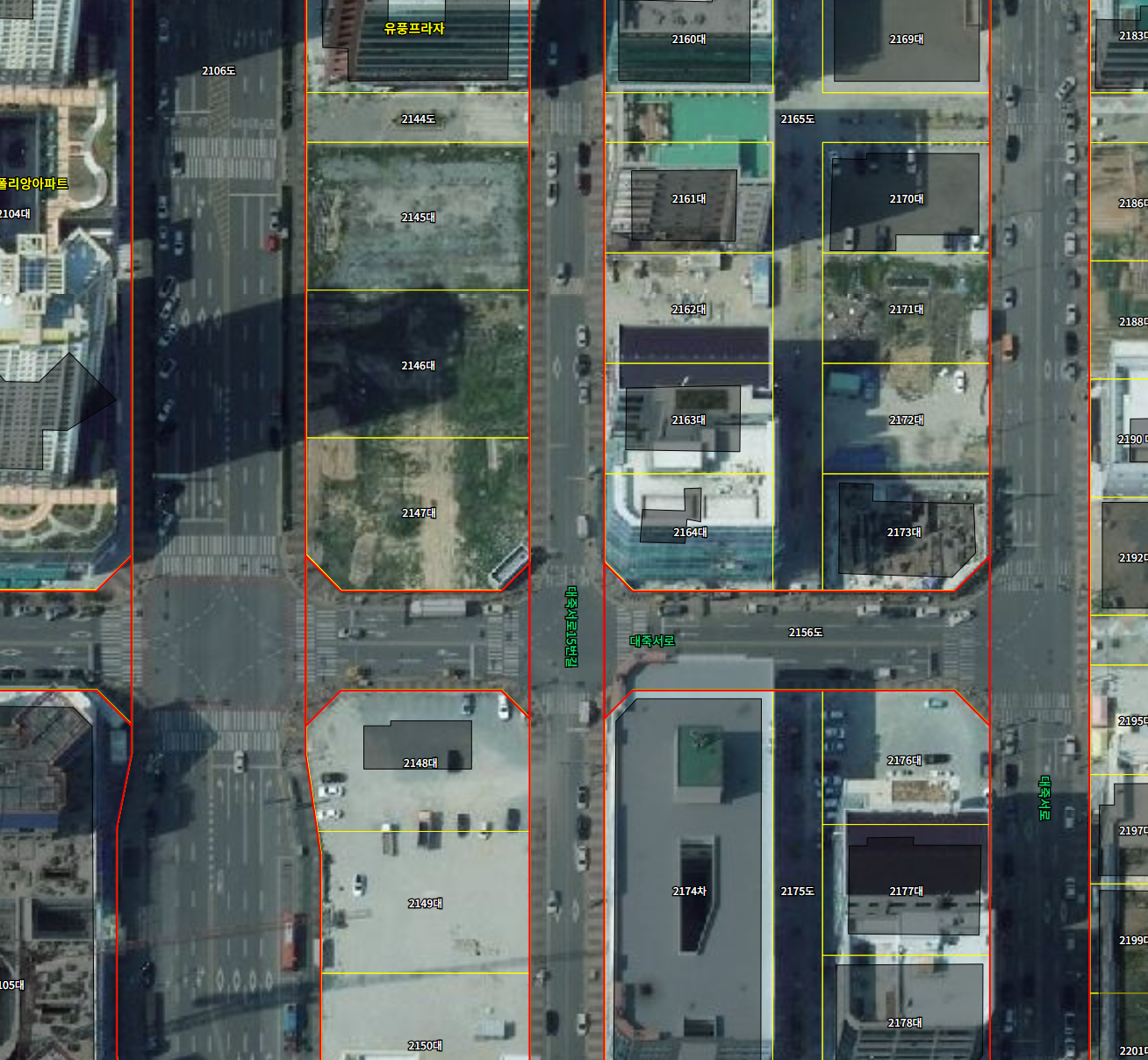
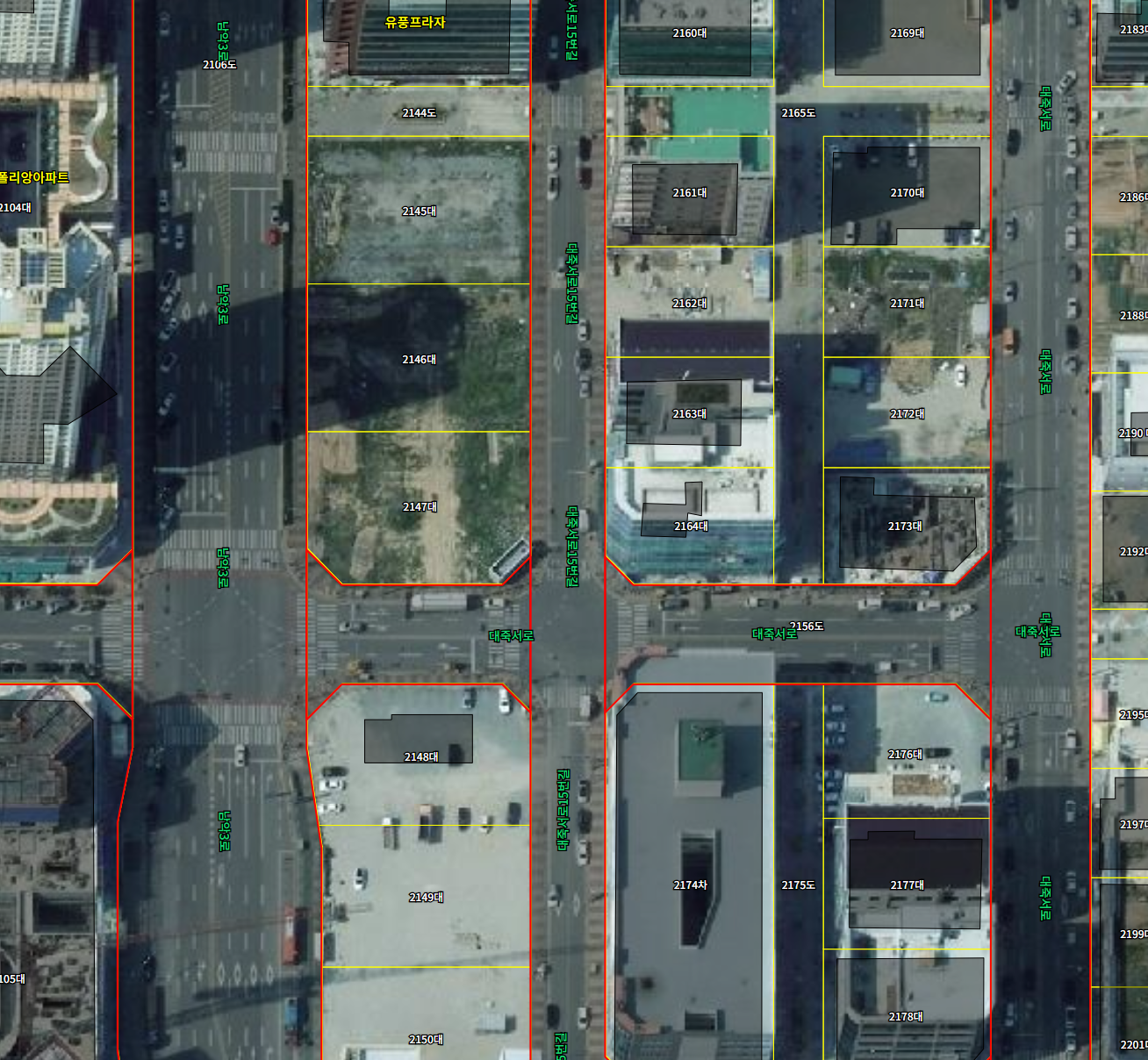
우리가 GIS를 활용해 무언가를 할 때 공간 데이터들 간의 좌표를 맞춰 레이어 단위로 중첩하여 하나의 지도를 구성한 뒤, 시각적 비교와 다양한 분석을 처리하게 됩니다. 이번에 경상북도 지역 중 내륙과 상당히 멀리 떨어져 있는 울릉도 지역에 대한 좌표계에 상당한 문제가 있다는 것을 파악했습니다. 독도는 더 심각!! -_-; 경상북도의 울릉도를 제외한 다른 지역은 그 좌표계가 매우 정확히 일치하는 것을 볼 때 울릉도 지역에 대한 좌표 불일치는 데이터 구축단계에서 원점 처리에 있어 상당한 문제가 있고, 근본적인 해결을 국가공간정보포털의 운영 주체인 정부 차원에서 조속히 해결해줘야 할 부분으로 생각합니다. 아래는 GRS80 UTM-K 좌표계로 변환하여 지적도와 행정경계를 중첩한 지도입니다.
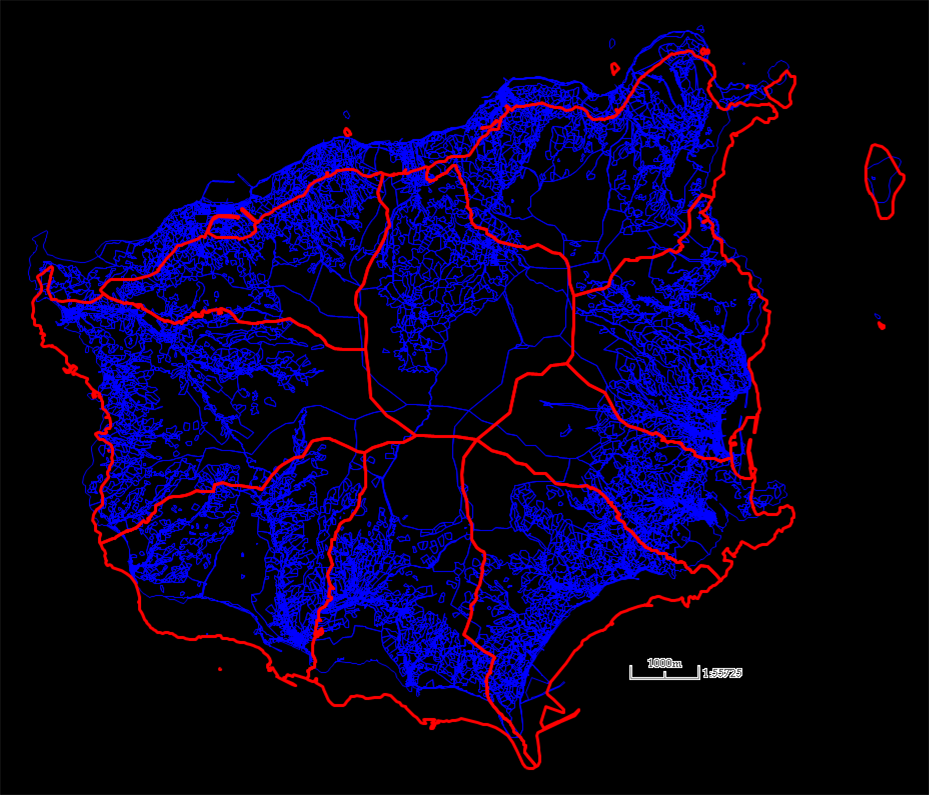
앞서 언급하였듯이, 을릉도 이외의 다른 경상북도 지역은 GRS80 UTM-K 좌표계로 변환하여 중첩했을 경우 정확히 일치합니다. 제대로 구축된 데이터를 구할 수 있다면 좋았겠지만, 그럴 수 없는 상황에서 이처럼 구축 단계에서 근본적으로 잘못 되어진 공간 데이터의 좌표계를 일치시키는 방법으로 Georeferencing 기능을 활용하는 방법밖에 없었고, Georeferencing 기능을 수행할 수 있는 GDAL의 ogr2ogr.exe 콘솔 프로그램을 사용하고자 하였습니다. 그런데 이 프로그램은 콘솔인지라, 시각적으로 GCP를 잡을 수 없다는 문제가 있습니다. QGIS을 활용해 보려고 하였으나, 관련된 기능에 오류가 발생합니다. QGIS 역시 GDAL의 기능을 그대로 활용하면서 단지 시각적으로 GCP를 잡는 기능을 제공하는 것으로 예상됩니다. 여튼.. ogr2ogr을 통한 Georeferencing 기능을 위해 시각적으로 GCP를 효과적을 취득할 수 있는 툴을 별도로 개발하였고 아래의 화면과 같습니다.
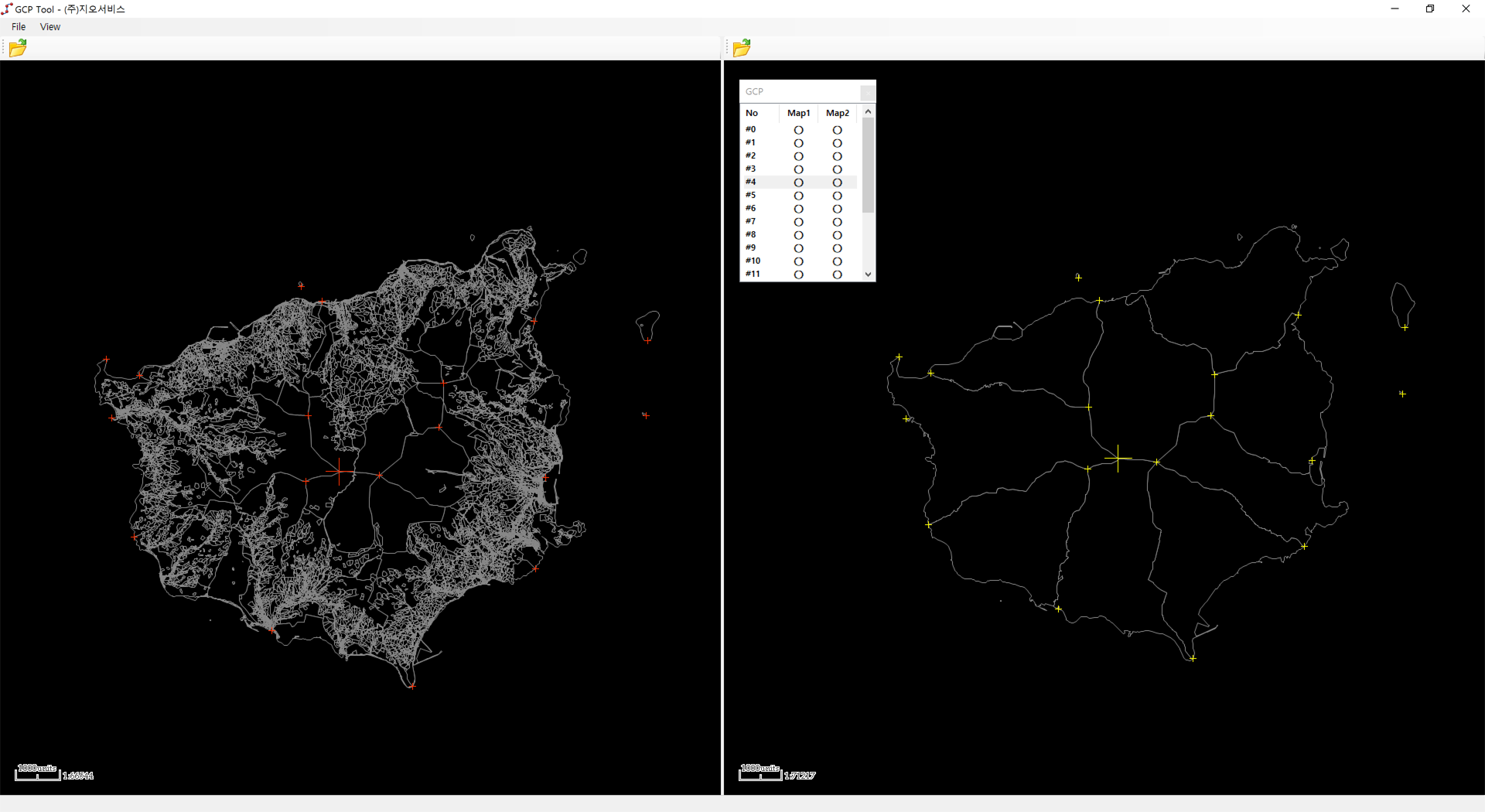
위의 프로그램을 통해 19개의 GCP 좌표를 입력하여 Georeferencing 기능을 수행하여 얻은 결과는 아래와 같습니다.

그러나 이러한 수치지도에 대한 Georeferencing 방식을 활용하여 좌표계 일치하는 방법은 최선의 방법이 아닙니다. Georeferencing은 원래 목적은 항공영상과 같은 이미지를 수치지도에 맵핑시키기 위한 방법입니다. 결과적으로 수치지도를 또 다른 수치지도와 맵핑시키는 Georeferencing 방식은 그 결과면에서 정확도가 매우 떨어집니다. 근본적인 방법은 공간 데이터 구축을 처음부터 올바르게 해서 제공해야 한다는 것입니다. 조속히 관련 기관에서 해결해 주기를 바랄 뿐입니다.