이 글의 원문은 https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_histograms/py_histogram_equalization/py_histogram_equalization.html#histogram-equalization 입니다.
히스토그램을 활용하여 이미지의 품질을 개선하기 위한 방법이 히스토그램 균등화(Equalization)입니다. 이해를 돕기 위해 아래의 코드를 살펴보면..
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('./data/wiki.jpg', 0)
hist,bins = np.histogram(img.flatten(),256,[0,256])
#cdf = hist.cumsum()
#cdf_m = np.ma.masked_equal(cdf,0)
#cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())
#cdf = np.ma.filled(cdf_m,0).astype('uint8')
#img = cdf[img]
cv2.imshow('img', img)
plt.hist(img.flatten(),256,[0,256], color = 'r')
plt.xlim([0,256])
plt.show()
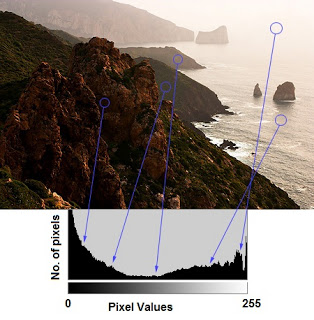
결과는 다음과 같습니다.
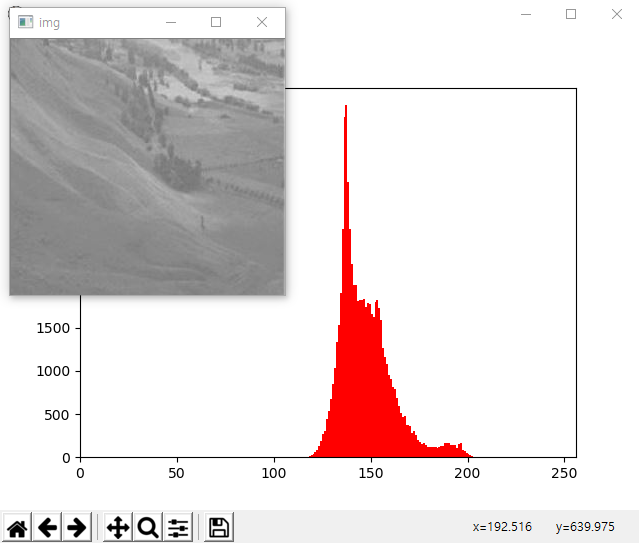
이미지의 화소값이 0-255에 걸쳐 균등하게 분포하지 못하고 120-210 정도 사이에 밀집되어 있어 있습니다. 이 이미지의 품질을 히스토그램 균동화 방법을 이용해 개선해 보겠습니다. 먼저 numpy를 이용한 코드입니다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('./data/wiki.jpg', 0)
hist,bins = np.histogram(img.flatten(),256,[0,256])
cdf = hist.cumsum()
cdf_m = np.ma.masked_equal(cdf,0)
cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())
cdf = np.ma.filled(cdf_m,0).astype('uint8')
img = cdf[img]
cv2.imshow('img', img)
plt.hist(img.flatten(),256,[0,256], color = 'r')
plt.xlim([0,256])
plt.show()
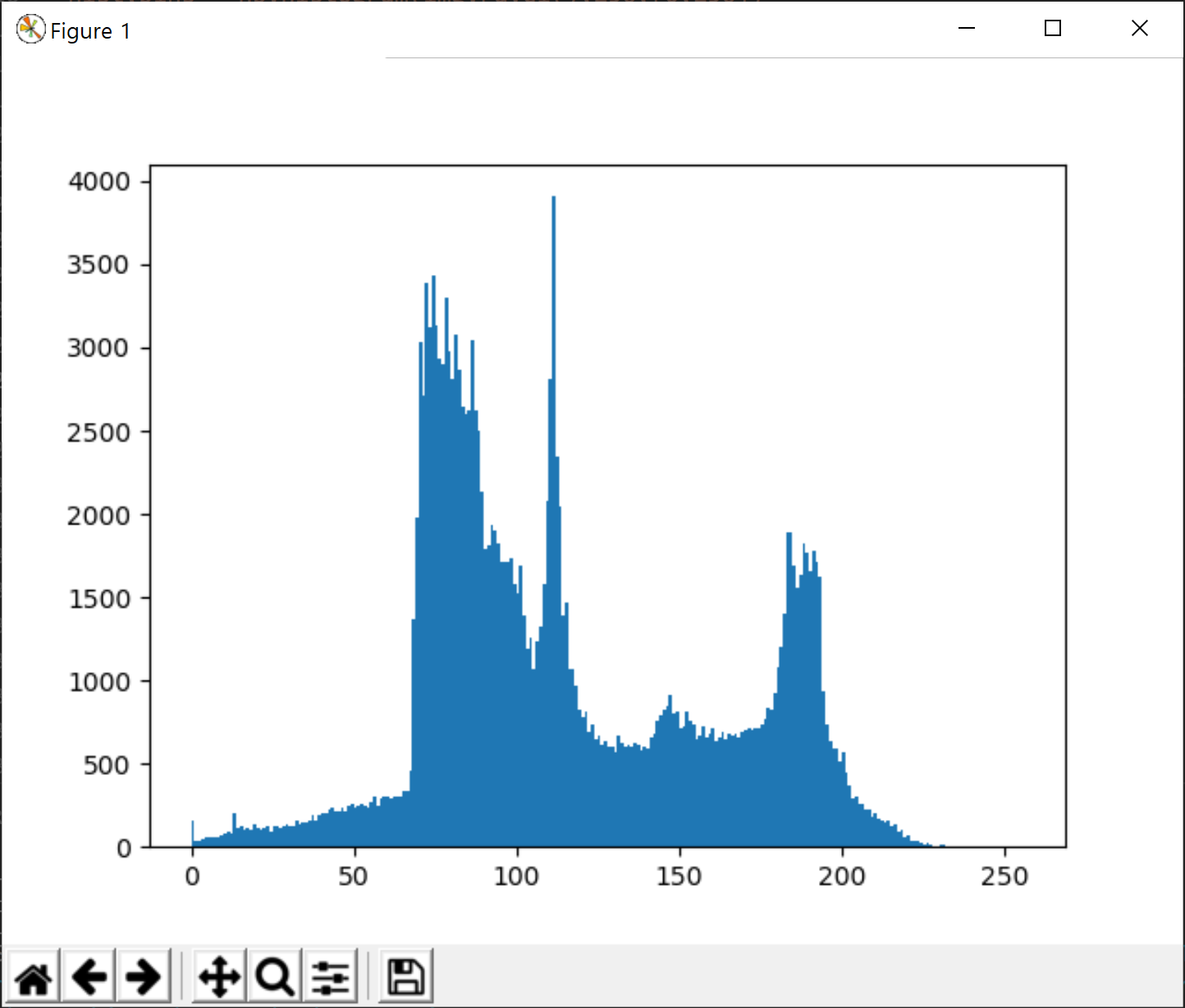
결과는 다음과 같습니다.
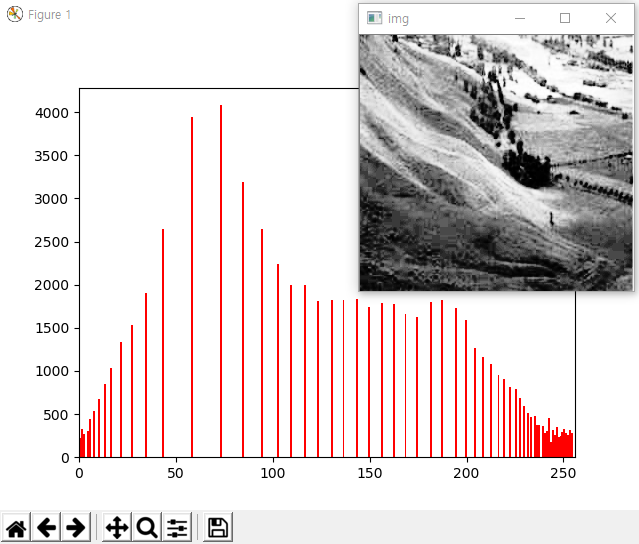
뿌옇게 보였던 이미지가 좀더 명확이 보이고 있습니다. 이유는 위의 이미지의 히스토그램 그래프처럼 화소값이 0-255 사이에 고루게 분포하고 있습니다.
OpenCV의 함수를 이용한 방식에 대한 코드는 다음과 같습니다.
import cv2
import numpy as np
img = cv2.imread('./data/tsukuba_l_clr.png',0)
equ = cv2.equalizeHist(img)
res = np.hstack((img,equ)) #stacking images side-by-side
cv2.imshow('img', res)
cv2.waitKey()
cv2.destroyAllWindows()
결과는 다음과 같습니다.

왼쪽은 원본이고 오른쪽이 히스토그램 균등화를 통한 이미지입니다. 이미지가 명확해지긴했으나 석고상의 밝기값이 너무 큽니다. 이는 이미지가 전체적으로 빛이 고르게 비치지 못하고 석고상에 상대적으로 더 많은 빛이 비춰졌기 때문입니다. 이를 위해서는 히스토그램 균등화를 이미지 전체에 대해 적용하는게 아닌 일정한 영역을 분리하여 해당 영역에 대한 히스토그램 균등화 연산을 수행해 그 결과를 조합하면 됩니다. 이러한 알고리즘을 CLAHE(Contrast Limited Adaptive Histogram Equalization)라고 하는데, 해당 코드는 다음과 같습니다.
import cv2
import numpy as np
img = cv2.imread('./data/tsukuba_l_clr.png',0)
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
res = np.hstack((img,cl1)) #stacking images side-by-side
cv2.imshow('img', res)
cv2.waitKey()
cv2.destroyAllWindows()
결과는 다음과 같습니다.

CLAHE 알고리즘을 구현한 cv2.createCLAHE 함수에서 tileGridSize=(8,8)이라는 의미는 8×8 격자 크기의 영역을 사용한다는 것입니다.