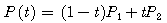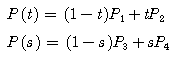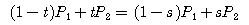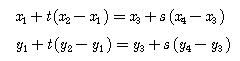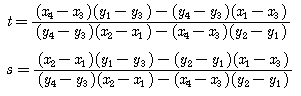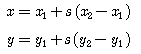GIS 엔진은 내부적으로 엄청난 수의 도형을 검색하여 화면에 그리는데, 추구하는 목표는 얼마나 빠르게 검색하여 얼마나 빨리 그리느냐는 것. 이것은 로컬에 대한 경우이고 서버와 클라이언트의 개념으로 확장하면 신속한 검색과 빠른 그리기는 기본이고 추가적으로 서버가 얼마나 빠르게 클라이언트로 도형의 좌표 데이터를 전송하는가까지 고민해 봐야 한다. 그리기에 한정해서 볼때, 윈도우즈 GDI API는 윈도우즈 운영체제 초기버전부터 지금까지 지속적으로 개선되고 발전해 왔으며 GDI+로 대체되는 듯 하지만, 여전히 속도를 요구하는 부분에서는 GDI+ 보다는 GDI를 사용한다. 이러한 GDI API를 이용하여 폴리라인을 그릴때, 화면을 벗어나는 폴리라인을 무시하고 화면에 보이는 폴리라인만 따로 계산하여 그려야할 필요가 없을 정도로 GDI API는 실패하지 않고 성공적으로 또한 빠르게 작동한다. 하나의 예로 아래의 그림과 같은 상황에서도 무리없이 폴리라인을 그려낼 수 있다.
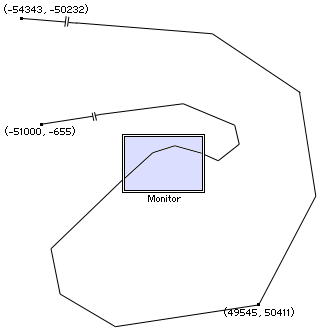
즉, 위의 폴리라인의 구성좌표(좌표값이 몇만단위)를 그대로 GDI API를 사용하여 그려도 얼마간의, 그러나 충분히 무시할 수 있는 성능의 희생만으로 화면상에 빠르게 그릴 수 있다.
그런데 왜 필자가 폴리라인을 사각영역에 대해 클리핑하는 방법을 필요로 했는가? 이유는 오렌지맵을 네트워크 버전으로 확장하면서 폴리라인이나 폴리곤을 임이의 사각영역에 대해 클리핑 해야만 한다는 절대적인 필요성을 느꼈기 때문이다. 즉, 클라이언트에서 서버에게 자신의 화면영역을 전달하면 서버는 그 영역에 해당하는 도형을 신속하게 검색하여 클라이언트에게 검색된 도형의 좌표들을 전송해준다. 이때, 검색된 도형의 좌표를 모두 전송하지 않고, 화면상(사각영역)에 들어가는 폴리라인의 좌표만을 전송해준다면 네트워크 상의 속도는 훨씬 더 향상될 것이다. 실제로 GIS에서는 등고선과 도로망도 등, 아주 긴 폴리라인을 아주 많이, 굉장이 많이 사용하게 되는데 꽤 이름이 알려진 상용 GIS 서버들 조차 이러한 경우에 매우 비효율적인 전송 방법, 즉 검색된 도형의 모든 좌표를 전송한다는 것이다. 대부분 GIS 서버들은 이러한 문제를 해결하기 위해서 폴리라인을 세그먼트화(폴리곤을 일정한 간격으로 계속 자르는 방법)하여 해결한다. 그러나 이러한 데이터를 재처리하는 방법은 불필요한 좌표 중복이 심하게 발생하는데, 이는 세그먼트화된 폴리라인들은 서로 시작 좌표와 끝 좌표를 중복하여 유지해야 하기 때문이다. 이러한 GIS 데이터 차원에서의 해결이 아닌 프로그램에서의 처리방법이 바로 폴리라인의 클리핑이다. 참고로 아래의 알고리즘은 필자가 개발하고 있는 오렌지박스 Map 서버에서 실제로 사용하였으며 등고선과 같은 데이터의 경우, 서버가 클라이언트로 전송해야할 데이터의 크기를 획기적으로 줄일 수 있었다.
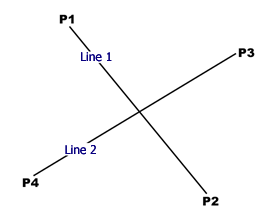
대상이 되는 폴리라인과 기준이 되는 사각영역을 아래의 그림을 예로 들어 설명한다.
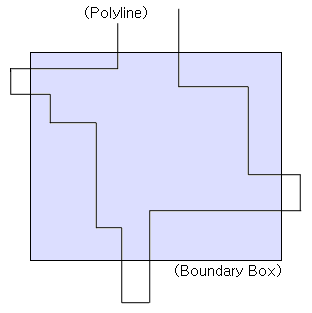
위의 그림을 보면 하나의 폴리라인이 사각영역에 의해 클리핑되어 4개의 폴리라인이 되는 것을 알 수 있다. 클리핑 되기전의 폴리라인은 총 17개의 시작점과 끝점으로 구성된 선으로 이루어져 있고, 사각영역은 4개의 선으로 이루어져 있다. 선과 선의 교차 알고리즘(본 블로그에 있음)을 이용하여 사각영역을 구성하는 선과 폴리라인과의 교차점(아래 그림의 빨간색점)을 구할 수 있다.
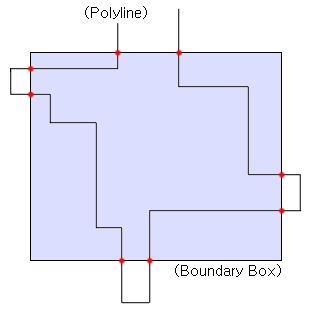
위의 그림을 보면 클리핑된 폴리라인의 시작점과 끝점의 사격영역과 폴리라인의 교차점이라는 사실을 알 수 있다. 하지만 예외가 있는데 아래의 그림이 바로 그 예외이다.
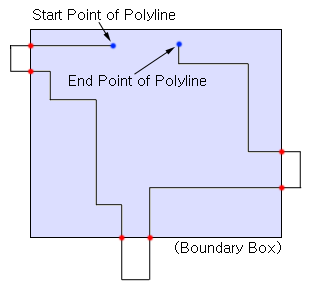
즉, 폴리라인의 시작점이나 끝점이 사각영역의 내부에 위치할 경우 클리핑된 폴리라인의 시작점과 끝점이 교차점이 아니라는 예외가 발생한다. 하지만 이런 예외는 단순히 클리핑되기 이전의 폴리라인의 시작점과 끝점이 사각영역 내부에 있을 경우 교차점으로 판정한다고 결정하면 해결된다.
자, 이제 위에서 언급한 내용을 토대로 실제로 클립핑된 폴리라인들의 좌표를 구성하는 과정을 단계별로 그림으로 살펴보자.
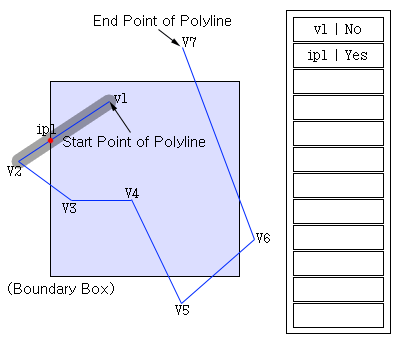
첫단계인 위의 그림에서 처럼, 먼저 폴리라인을 구성하는 첫 라인에 대해서 사각영역과의 교차점을 구한다. 여기서 첫 라인의 시작점이 경계상자 안에 위치하므로 내부버퍼에 저장하고 교차점도 저장한다. 그러나 끝점은 경계상자의 밖에 위치하므로 버린다. 내부 버퍼에 저장된 좌표와 상태를 위의 그림과 함께 나타내었다. 내부 버퍼의 상태에서 Yes와 No는 각각 해당 좌표가 교차점인가 아닌가를 나타내는 것이다.
두번째 단계에 대한 그림은 아래와 같다.
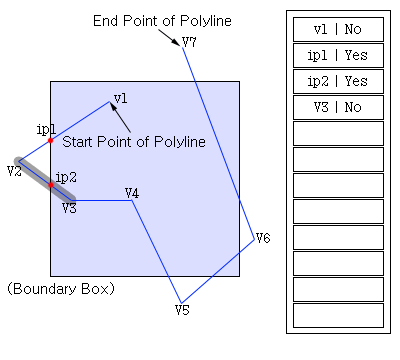
선의 시작점인 V2는 경계상자의 밖에 위치하므로 무시하고 끝점인 V3는 경계상자의 안에 위치하므로 내부버퍼에 저장한다. 물론 V3를 저장하기에 앞서 교차점인 ip2를 저장해야한다.
세번째 단계에 대한 그림은 아래와 같다.
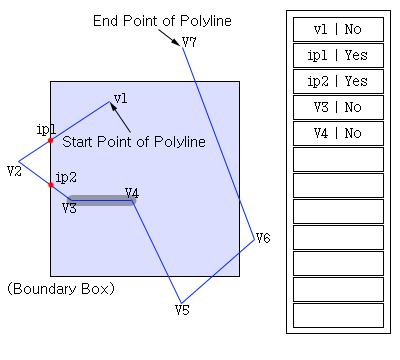
세번째 단계는 선의 시작점과 끝점 모두 경계상자 내부에 위치하는 경우이므로 두점 모두 유효하다. 그러나 시작점은 이미 버퍼에 저장된 최근 좌표와 중복되므로 무시할 수 있다. 이때 저장되 최근 좌표의 종류가 교차점이라면 무시해서는 않된다.
네번째 단계는 첫번째 단계와 동일하므로 설명을 생략하고 다섯번째 단계를 살펴보면….
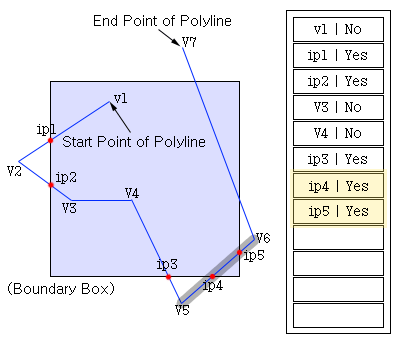
선의 시작점과 끝점이 모두 경계상자 밖에 위치하므로 교차점은 없거나 두개가 생기게 된다. 교차점이 없다면 내부버퍼에 저장할 것이 없지만 교차점이 두개인 경우 그 두개의 교차점을 내부 버퍼에 저장한다. 이때 중요한 것은 시작점과 가까운 교차점을 먼저 저장해야한다.
이제 마지막 선에 대해 계산을 해보면…
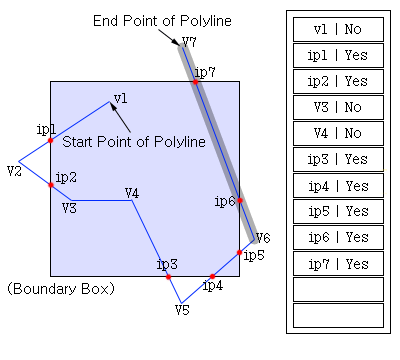
마지막 단계는 이전 단계와 같은 상황이므로 따로 설명할 필요는 없는 듯하다.
이제 폴리라인의 모든 선분들에 대해서 계산을 끝낸 최종결과가 내부버퍼에 저장되어져 있으므로 이 버퍼를 이용해 클리핑된 폴리라인을 알 수 있다. 서두에서 언급했던 것처럼 내부 버퍼의 시작과 끝 좌표요소을 교차점으로 간주하기로 했다는 것을 잊지 말기 바란다. 즉 내부 버퍼는 최종적으로 아래와 같은 상태가 될것이다.
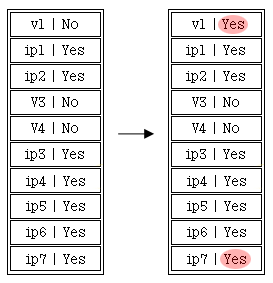
위의 최종 버퍼를 통해 폴리라인을 그리거나, 좌표를 구할 수 있다. 처음 Yes의 좌표는 폴리라인이 시작점이 되고 그 다음의 Yes를 만날때까지 동일한 폴리라인의 구성점이 되다가 Yes를 만나면 동일한 폴리라인의 끝점이 된다.
이상으로 폴리라인의 사격영역에 대한 클리핑 알고리즘에 대한 설명을 끝마친다.
이 알고리즘은 필자가 나름대로 고민하여 구상한 알고리즘으로 기존의 더 나은 알고리즘도 있을 것이다. 하지만 필자가 스스로 고민하여 만들어낸 알고리즘을 실제 프로그램상에 적용하여 만족할 만한 결과를 얻어낸 알고리즘이라는 점을 강조하고 싶다.